习题课内容
第1章 流体流动
1.1 流体的物理性质
- 流体的静压强:
- 流体的单位表面积上所受的压力,称为流体的静压强,简称压强。
- 表压强 = 绝对压强 - 大气压强。
- 真空度 = 大气压强 - 绝对压强 = -表压强。
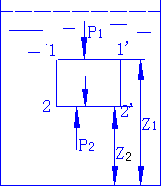
- 流体静力学方程:
- 推导:在1-1'截面受到垂直向下的压力\(F_1 = p_1A\),在2-2'截面受到垂直向上的压力\(F_2 = p_2A\),小液柱本身所受的重力\(W = mg = \rho Vg = \rho A(z_1 - z_2)g\)。因为小液柱处于静止状态,\(F_2 - F_1 - \rho A(z_1 - z_2)g = 0\)。
- 流体静力学方程:\(p = p_0 + \rho gh\),表明在重力作用下,静止液体内部压强的变化规律。
- 方程的讨论:
- 液体内部压强\(p\)是随\(p_0\)和\(h\)的改变而改变的,即\(p = f(p_0, h)\)。
- 当容器液面上方\(p_0\)一定时,静止液体内部的压强仅与垂直距离\(h\)有关,即\(p \propto h\)。处于同一水平面上各点的压强相等。
- 当液面上方的压强改变时,液体内部的压强也随之改变,即:液面上所受的压强能以同样大小传递到液体内部的任一点。
- 从流体静力学的推导可以看出,它们只能用于静止连通着的同一种流体的内部,对于间断的并非单一流体的内部则不满足这一关系。
- \(p = p_0 + \rho gh\)可以改写成\(\cfrac {p - p_0}{\rho g} = h\),压强差的大小可利用一定高度的液体柱来表示,这就是液体压强计的根据,在使用液柱高度来表示压强或压强差时,需指明何种液体。
- 方程是以不可压缩流体推导出来的,对于可压缩性的气体,只适用于压强变化不大的情况。
- 静力学方程的应用:
- 压强与压强差的测量
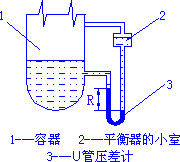
 U型管压差计:\(p_a = p_{a'}\),根据流体静力学方程,\(p_a = p_1 + \rho_Bg(m + R)\),\(p_{a'} = p_2 + \rho_B g(z + m) + \rho_A gR\),则\(p_1 - p_2 = (\rho_A - \rho_B)gR + \rho_AgZ\)。
U型管压差计:\(p_a = p_{a'}\),根据流体静力学方程,\(p_a = p_1 + \rho_Bg(m + R)\),\(p_{a'} = p_2 + \rho_B g(z + m) + \rho_A gR\),则\(p_1 - p_2 = (\rho_A - \rho_B)gR + \rho_AgZ\)。
当管子平放时,\(p_1 - p_2 = (\rho_A - \rho_B)gR\),此为两点间压差计算公式。
当被测的流体为气体时,\(\rho_A \gg \rho_B\),\(\rho_B\)可以忽略,则\(p_1 - p_2 \approx \rho_A gR\)。
若U型管的一段与被测流体相连接,另一端与大气相通,那么读数\(R\)就反映了被测流体的绝对压强与大气压之差,也就是被测流体的表压。
当\(p_1 - p_2\)值较小时,\(R\)值也较小,若希望读数\(R\)清晰,可采取三种措施:两种指示液的密度差尽可能减小、采用倾斜U型管压差计、采用微差压差计。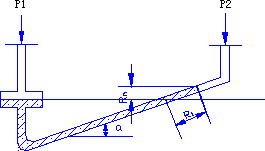 倾斜U型管压差计:假设垂直方向上的高度为\(R_m\),读数为\(R_1\),与水平倾斜角度为\(\alpha\),则\(R_1 = \cfrac {R_m}{\sin \alpha}\)。
倾斜U型管压差计:假设垂直方向上的高度为\(R_m\),读数为\(R_1\),与水平倾斜角度为\(\alpha\),则\(R_1 = \cfrac {R_m}{\sin \alpha}\)。- 微差压差计:U型管的两侧管的顶端增设两个小扩大室,其内径与U型管的内径之比 > 10,装入两种密度接近且互不相溶的指示液A和C,且指示液C与被测流体B亦不互溶,则\(p_1 - p_2 = (\rho_A - \rho_C)gR\)。
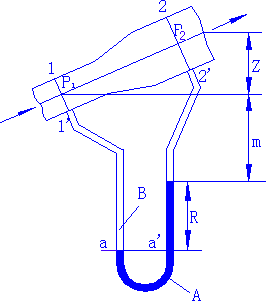
- 液位的测定:
- 液位计的原理:遵循静止液体内部压强变化的规律,是静力学基本方程的一种应用。
 液柱压差计测量液位的方法:由压差计指示液的读数\(R\)可以计算出容器内页面的高度。当\(R = 0\)时,容器的页面高度将达到允许的最大高度;容器内页面越低,压差计读数\(R\)越大。
液柱压差计测量液位的方法:由压差计指示液的读数\(R\)可以计算出容器内页面的高度。当\(R = 0\)时,容器的页面高度将达到允许的最大高度;容器内页面越低,压差计读数\(R\)越大。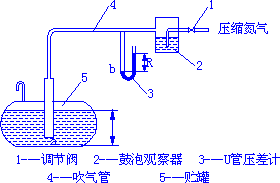 远距离控制液位的方法:压缩氮气自管口经调节阀通入,调节气体的流量使气流速度极小,只要在鼓泡观察室内看出有气泡缓慢逸出即可。
远距离控制液位的方法:压缩氮气自管口经调节阀通入,调节气体的流量使气流速度极小,只要在鼓泡观察室内看出有气泡缓慢逸出即可。
压差计读数\(R\)的大小,反映出贮罐内液面的高度。
- 液封高度的计算:
- 液封的作用:
若设备内要求气体的压力不超过某种限度时,液封的作用是当气体压力超过这个限度时,气体冲破液封流出,又称为安全性液封。
若设备内为负压操作,其作用是防止外界空气进入设备内。
液封需有一定的液位,其高度的确定就是根据流体静力学基本方程式。
- 液封的作用:
- 压强与压强差的测量
1.2 流体流动的基本方程
- 流量与流速
- 流量:单位时间内流过管道任一截面的流体量。若用体积来计量称为体积流量\(V_{\text{s}}\),若用质量来计量称为质量流量\(w_{\text{s}}\),\(w_{\text{s}} = V_{\text{s}}\rho\)。
- 流速:单位时间内流体在流动方向上流过的距离。\(u = \cfrac {V_{\text{s}}}{A}\)。
- 流量与流速的关系:\(v_{\text{s}} = uA\),\(w_{\text{s}} = uA\rho\)。
- 质量流速:单位时间内流体流过管道单位面积的质量流量。\(G = \cfrac {w_{\text{s}}}{A} = \cfrac {V_{\text{s}}\rho}{A} = u\rho\)。
- 对于圆形管道,\(A = \cfrac {\pi}{4}d^2\),\(u = \cfrac {4V_{\text{s}}}{\pi d^2}\),\(d = \sqrt{\cfrac {4V_{\text{s}}}{\pi u}}\)。
- 连续性方程:
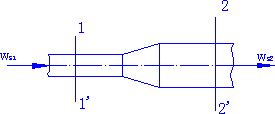 在稳定流动系统中,对直径不同的管段做物料衡算,对于连续稳定系统输入 = 输出,即\(w_{\text{s}1} = w_{\text{s}2}\)。
在稳定流动系统中,对直径不同的管段做物料衡算,对于连续稳定系统输入 = 输出,即\(w_{\text{s}1} = w_{\text{s}2}\)。- 推广到任意截面,有\(w_{\text{s}} = uA\rho = \text{常数}\)。
- 若流体为不可压缩流体,则有\(V_{\text{s}} = uA = \text{常数}\)。
对于圆形管道,\(\cfrac {u_1}{u_2} = \left(\cfrac {d_2}{d_1}\right)^2\),表明当体积流量一定时,管内流体的流速与管道直径的平方成反比。
- 能量衡算方程式:
- 流体流动的总能量衡算:
- 流体本身具有的能量:
内能:物质内部能量的总和称为内能。单位质量流体的内能以\(U\)表示。
位能:流体因处于重力场内而具有的能量。质量为\(m\)、高度为\(Z\)的流体具有的位能为\(mgZ\)。
动能:流体以一定的流速流动而具有的能量。质量为\(m\)、流速为\(u\)的流体所具有的动能为\(\frac 12mu^2\)。
静压能:通过某截面的流体具有的用于克服压力功的能量。流体通过截面的静压能为\(pV\),单位质量流体所具有的静压能\(p\cfrac {V}{m} = pv\)。其中\(v\)为比容。
单位流体本身所具有的总能量为:\(U + gZ + \frac 12u^2 + pv\),单位为J/kg。 - 系统与外界交换的能量:
热:单位质量流体通过划定体积的过程中所吸的热为\(q_{\text{e}}\),吸热为正,放热为负。
外功:单位质量通过划定体积的过程中接受的功为\(w_{\text{e}}\),接受外功为正,向外做功为负。
流体本身所具有能量和热、功就是流动系统的总能量。 - 总能量衡算:\(\Delta U + g\Delta z + \cfrac {\Delta u^2}{2} + \Delta(pv) = q_{\text{e}} + w_{\text{e}}\)。
\(H = U + pv\),\(\Delta H + g\Delta Z + \cfrac {\Delta u^2}{2} = q_{\text{e}} + W_{\text{e}}\)。
- 流体本身具有的能量:
- 流体系统的机械能恒算式:\(g\Delta Z + \cfrac {\Delta u^2}{2} + \int_{p_1}^{p_2}v\mathrm dp = W_{\text{e}} - \sum h_{\text{f}}\),其中\(\sum h_{\text{f}}\)为流体克服流动阻力而损失的能量。
- 伯努利方程:当流体不可压缩时有\(g\Delta Z + \cfrac {\Delta u^2}{2} + \cfrac{\Delta p}{\rho} = W_{\text{e}} - \sum h_{\text{f}}\);或\(gZ_1 + \cfrac {u_1^2}{2} + \cfrac {p_1}{\rho} + W_{\text{e}} = gZ_2 + \cfrac {u_2^2}{2} + \cfrac {p_2}{\rho} + \sum h_{\text{f}}\)。
- 伯努利方程的讨论:
- 理想流体在管内做稳定流动、没有外功加入时,任意截面上单位质量流体的总机械能即动能、位能、静压能之和为一常数(总机械能),用\(E\)表示。各种形式的机械能可以相互转换。
- 对于实际流体,上游截面处的总机械能大于下游截面处的总机械能。
- 式中\(g\Delta z\)、\(\cfrac {\Delta u^2}{2}\)、\(\cfrac {\Delta p}{\rho}\)为处于某个截面上的流体本身所具有的能量,\(W_{\text{e}}\)和\(\sum h_{\text{f}}\)为流体流动过程中获得或消耗的能量。
\(N_{\text{e}}\)为单位时间输送设备对流体所做的有效功,即有效功率。\(N_{\text{e}} = W_{\text{e}}w_{\text{s}} = W_{\text{e}}V_{\text{s}}\rho\)。 - 当体系无外功且处于静止状态时有\(gZ_1 + \cfrac {p_1}{\rho} = gZ_2 + \cfrac {p_2}{\rho}\),流体的静力平衡是流体流动状态的一个特例。
- 对于可压缩流体的流动,当所取系统两截面之间的绝对压强变化小于原来压强的20%,即\(\cfrac {p_1 - p_2}{p_1} < 0.2\)时,仍可使用伯努利方程。式中流体密度应以两截面之间流体的平均密度\(\rho_{\text{m}}\)代替。
- 若以单位重量的流体为衡算标准,\(Z_1 + \cfrac {u_1^2}{2g} + \cfrac {p_1}{\rho g} + H_{\text{e}} = Z_2 + \cfrac {u_2^2}{2g} + \cfrac {p_2}{\rho g} + H_{\text{f}}\),其中\(H_{\text{e}} = \cfrac {W_{\text{e}}}{g}\),\(H_{\text{f}} = \cfrac{\sum H_{\text{f}}}{g}\)。,\(Z\)、\(\cfrac {u^2}{2g}\)、\(\cfrac {u^2}{\rho g}\)和\(H_{\text{f}}\)分别被称为位压头、动压头、静压头和压头损失,\(H_{\text{e}}\)为输送设备对流体所提供的有效压头。
若以单位体积流体为衡算标准,\(\rho gZ_1 + \cfrac {\rho u_1^2}{2g} + p_1 + W_{\text{e}}\rho = \rho gZ_2 + \cfrac {\rho u_2^2}{2g} + p_2 + \rho\sum h_{\text{f}}\) - 对于非稳态流动系统的任意瞬间,伯努利方程仍然成立。
- 流体流动的总能量衡算:
- 伯努利方程式的应用:
- 作图并确定衡算范围:根据题意画出流动系统的示意图,并指明流体的流动方向,定出上下截面,以明确流动系统的衡标范围。
- 截面的截取:两截面都应与流动方向垂直,并且两截面的流体必须是连续的,所求得未知量应在两截面或两截面之间,截面的有关物理量\(Z\)、\(u\)、\(p\)等除了所求的物理量之外,都必须是已知的或者可以通过其它关系式计算出来。
- 基准水平面的选取:基准水平面的位置可以任意选取,但必须与地面平行,为了计算方便,通常取基准水平面通过衡算范围的两个截面中的任意一个截面。如衡算范围为水平管道,则基准水平面通过管道中心线,\(\Delta Z = 0\)。
- 单位必须一致:在应用柏努利方程之前,应把有关的物理量换算成一致的单位,然后进行计算。两截面的压强除要求单位一致外,还要求表示方法一致。
第2章 流体输送机械
2.1 流体输送机械
- 离心泵的基本方程式:
- 基本假设:
- 泵叶轮的叶片数目为无限多个。
- 输送的是理想液体,流动中无流动阻力。
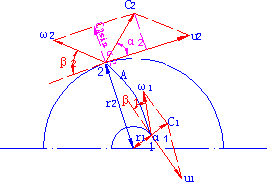 推导:
推导:
- 在高速旋转的叶轮当中,液体质点的运动包括:液体随叶轮旋转;经叶轮流道向外流动。
- 液体与叶轮一起旋转的速度\(u_1\)、\(u_2\)方向与所处圆周的切线方向一致,大小为\(u = \cfrac {2\pi r n}{60}\)。
- 液体沿叶片表面运动的速度\(\omega_1\)、\(\omega_2\),方向为液体质点所处叶片的切线方向,大小与液体的流量、流道的形状等有关。
- 两个速度的合成速度\(c_1\)、\(c_2\)是液体质点在点1或点2处相对于静止的壳体的速度,称为绝对速度。
- 单位重量理想液体通过无数叶片的旋转获得的能量称作理论压头,用\(H_{\infty}\)表示。\(H_{\infty} = H_{\text{p}} + H_{\text{c}} = \cfrac {p_2 - p_1}{\rho g} + \cfrac {c_2^2 - c_1^2}{\rho g}\),其中\(H_{\text{p}}\)和\(H_{\text{p}}\)分别时静压头和动压头的增加。
- 静压头增加主要来源于离心力做功和能量转换,整理得\(H_{\infty} = \cfrac {u_2c_2\cos \alpha_2 - u_1c_1\cos\alpha_1}{g}\)。设计中一般\(\alpha_1 = 90^\circ\),即\(\cos\alpha_1 = 0\),得到\(H_{\infty} = \cfrac {u_2c_2\cos \alpha_2}{g}\)。
- 讨论:
- 离心泵基本方程式:\(H_{\infty} = \cfrac {(r_2\omega)^2}{g} - \cfrac {\omega \cot \beta_2}{2\pi b_2 g}Q_{\text{T}}\)。
对于某个离心泵,转速\(\omega\)一定时,理论压头与理论流量之间为线性关系,可表示为:\(H_{\infty} = A - BQ_{\text{T}}\)。 - 当叶片几何尺寸与理论流量一定时,离心泵的理论压头随叶轮的转速或直径的增加而增大。
- 根据流动角\(\beta_2\)的大小,可将叶片形状分为后弯(\(\beta < 90^\circ\))、径向(\(\beta = 90^\circ\))和前弯(\(\beta > 90^\circ\))叶片3种。前弯叶片理论压头最大,但实际上多采用后弯叶片。
- 离心泵基本方程式:\(H_{\infty} = \cfrac {(r_2\omega)^2}{g} - \cfrac {\omega \cot \beta_2}{2\pi b_2 g}Q_{\text{T}}\)。
- 基本假设:
- 离心泵的主要性能参数与特性曲线
- 离心泵的性能参数:
- 流量\(Q\):离心泵在单位时间里排到管路系统的液体体积。单位m3/h。
- 压头\(H\):泵对单位重量的液体所提供的有效能量,又称为泵的扬程。单位m。离心泵的压头取决于泵的结构、转速、流量。理想条件\(H = \Delta Z + \cfrac {p_2 - p_1}{\rho g}\)。
- 效率\(\eta\):反应能量损失,是容积损失、水力损失、机械损失三者总和。与泵的大小、类型、制造精密程度和所输送液体的性质有关。
- 轴功率\(N\):电机输入离心泵的功率。
有效功率\(N_{\text{e}}\):排送到管道的液体从叶轮获得的功率。\(N_{\text{e}} = \eta N\)。\(N_{\text{e}} = QH\rho g\)。
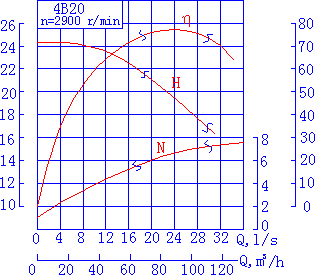 离心泵的特性曲线:\(H\)、\(\eta\)、\(N\)与\(Q\)的关系,随转速而变。由确定离心泵压头的实验来测定,实验测出。
离心泵的特性曲线:\(H\)、\(\eta\)、\(N\)与\(Q\)的关系,随转速而变。由确定离心泵压头的实验来测定,实验测出。
- \(H-Q\)曲线:压头随流量增大而下降。
- \(N-Q\)曲线:轴功率随流量增大而上升。
- \(\eta-Q\)曲线:效率随流量增大先上升到最大值,随后下降。
- 离心泵在一定转速下有最高效率点,在最高效率点对应的流量和压头下工作最为经济,此点的\(Q\)、\(H\)、\(N\)值称为最佳工况参数。
- 离心泵的性能参数:
- 离心泵的气蚀现象与允许吸上高度:
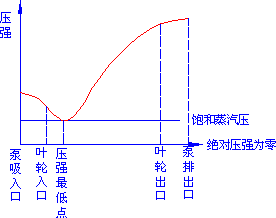 气蚀现象:叶片入口处的压强小于或低于输送温度下液体的饱和蒸气压。
气蚀现象:叶片入口处的压强小于或低于输送温度下液体的饱和蒸气压。
- 后果:产生噪音和震动,叶轮局部在巨大冲击的反复作用下,表面出现斑痕及裂纹,甚至呈海棉状逐渐脱落;液体流量明显下降,同时压头、效率也大幅度降低,严重时会输不出液体。
- 离心泵的允许吸上高度\(H_{\text{g}}\):又称为允许安装高度,指泵的吸入口与吸入贮槽液面间可允许达到的最大垂直距离。
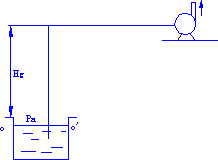 贮槽液面0-0'与入口处1-1'两截面间列柏努利方程:\(H_g = \cfrac {p_0 - p_1}{\rho g} - \cfrac {u_1^2}{2g} - H_{\text{f}0-1}\),若贮槽上方与大气相通,则\(p_0\)为大气压\(p_\text{a}\)。
贮槽液面0-0'与入口处1-1'两截面间列柏努利方程:\(H_g = \cfrac {p_0 - p_1}{\rho g} - \cfrac {u_1^2}{2g} - H_{\text{f}0-1}\),若贮槽上方与大气相通,则\(p_0\)为大气压\(p_\text{a}\)。
- 允许吸上真空度与允许安装高度:
- 允许吸上真空度:\(H_{\text{s}}' = \cfrac {p_{\text{a}} - p_1}{\rho g}\),通常以m液柱表示。
- 允许安装高度:\(H_{\text{g}} = H_{\text{s}}' - \cfrac {u_1^2}{2g} - H_{\text{f}0-1}\)。
- 气蚀余量:\(NPSH = \cfrac {p_1}{\rho g} + \cfrac {u_1^2}{2g} - \cfrac {p_{\text{v}}}{\rho g}\)。
- 允许安装高度:\(H_{\text{g}} = \cfrac {p_0 - p_{\text{v}}}{\rho g} - (NPSH)_{\text{r}} - H_{\text{f}0-1}\)
- 离心泵的并联和串联:
- 串联:两台相同型号的离心泵串联,在同样的流量下,其提供的压头是单台泵的两倍 。
- 并联:两台相同型号的离心泵并联,若其各自有相同的吸入管路,则在相同的压头下,并联泵的流量为单泵的两倍。
- 组合方式选择:对于低阻输送管路,并联优于串联;对于高阻输送管路,串联优于并联。
2.2 气体输送和压缩设备
- 离心通风机的性能参数与特性曲线
- 风量\(Q\):气体通过进风口的体积流率,气体的体积按进口状态计。
- 风压\(H_{\text{T}}\):单位体积的气体通过通风机时所获得的能量,与压强单位相同。取决于风机的结构,叶轮尺寸、转速与进入风机的气体的密度。无法理论计算,需要实验测定。
- 在通风机的进口截面和出口截面列伯努利方程:\(H_{\text{T}} = (p_2 - p_1) + \cfrac {\rho u^2}{2}\)。\(p_2 - p_1\)为静风压,\(\cfrac {\rho u^2}{2}\)为动风压。
- 风压与被输送气体的密度成正比,\(H_{\text{T}} = H_{\text{T}}' \cfrac {\rho}{\rho '}\)。
- 功率:离心通风机的轴功率为:\(N = \cfrac {H_{\text{T}}Q}{1000 \eta}\)。
第3章 非均相物系分离
3.1 颗粒及床层特性
- 颗粒的特性:
- 球形颗粒:体积\(V = \cfrac{\pi}{6}d^3\),表面积\(S = \pi d^2\),比表面积\(a = 6/d\)。
- 非球形颗粒:当量直径\(d_{\text{e}} = \sqrt[3]{\cfrac {6V_{\text{p}}}{\pi}}\),形状系数(球形度)\(\Phi_{\text{s}} = \cfrac {S}{S_{\text{p}}}\),其中\(S\)为与颗粒等体积圆球的表面积,\(S_{\text{p}}\)为颗粒实际表面积。
- 颗粒床层的特性:
- 空隙率:\(\varepsilon = \cfrac {床层体积 - 颗粒体积}{床层体积}\)。
- 床层的比表面积\(a_{\text{b}} = (1 - \varepsilon)a = \cfrac {6 \rho_{\text{b}}}{d \rho_{\text{s}}}\),其中\(\rho_{\text{b}}\)为堆积密度,\(\rho_{\text{s}}\)为真实密度,\(\rho_{\text{b}} = (1 - \varepsilon)\rho_{\text{s}}\)。
- 床层自由截面积:床层截面上可供流体通过的自由截面,即空隙截面与床层截面积之比,在数值上等于空隙率\(\varepsilon\)。
- 流体通过床层流动的压降:\(\cfrac {\Delta p_{\text{f}}}{L} = \lambda' \cfrac {(1 - \varepsilon)a}{\varepsilon^3} \rho u^2\)。
3.2 沉降分离
- 重力沉降:\(u_{\text{t}} = \sqrt{\cfrac {4dg(\rho_{\text{s}} - \rho)}{3\rho\zeta}}\)。
- 雷诺数:\(Re_{\text{t}} = \cfrac {du_{\text{t}}\rho}{\mu}\)。
- 阻力系数\(\zeta\):颗粒与流体相对运动时的雷诺数\(Re_{\text{t}}\)的函数。
- 滞流区/斯托克斯定律区(\(10^{-4} < Re_{\text{t}} < 1\)):\(\zeta = \cfrac {24}{Re_\text{t}}\),\(u_{\text{t}} = \cfrac {d^2(\rho_{\text{s}} - \rho)}{18\mu}\)。
- 过渡区/艾伦定律区(\(1 < Re_{\text{t}} < 10^3\)):\(\zeta = \cfrac {18.5}{Re_{\text{t}}^{0.6}}\),\(u_{\text{t}} = 0.269\sqrt{\cfrac {gd(\rho_{\text{s}} - \rho)Re_{\text{t}}^{0.6}}{\rho}}\)。
- 湍流区/牛顿定律区(\(10^3 < Re_{\text{t}} < 2 \times 10^5\)):\(\zeta = 0.44\),\(u_{\text{t}} = 1.74 \sqrt{\cfrac {d(\rho_{\text{s}} - \rho)g}{\rho}}\)。
- 沉降速度的计算:
- 试差法:假设沉降属于层流区,代入公式计算\(u_{\text{t}}\),反求\(Re\),如果满足\(Re_{\text{t}} < 1\)则求解正确,否则代入艾伦公式……
- 摩擦数群法。
- 降尘室:
- 降尘室内的颗粒运动:以速度\(u\)随气体流动、以速度\(u_{\text{t}}\)作沉降运动。沉降室使颗粒沉降的条件:\(\cfrac {l}{u} \ge \cfrac {H}{u_{\text{t}}}\)。降尘室的生产能力:\(V_{\text{s}} \le blu_{\text{t}}\)。
- 离心沉降:离心沉降速度\(u_{\text{r}} = \sqrt{\cfrac {4d(\rho_{\text{s}} - \rho)u_{\text{t}}^2}{3\zeta\rho R}}\),临界粒径\(d_{\text{c}} = \sqrt{\cfrac {9 \mu B}{\pi N \rho_{\text{s}}u_{\text{i}}}}\),压强降\(\Delta p = \cfrac {\zeta_{\text{c}}\rho u_{\text{i}}^2}{2}\)。
- 旋风分离器设计计算步骤:
- 根据具体情况选择合适的型式,选型时应在高效率与地阻力者之间作权衡,一般长、径比大且出入口截面小的设备效率高且阻力大,反之,阻力小效率低。
- 根据允许的压降确定气体在入口的流速\(u_{\text{i}}\)
- 根据分离效率或除尘要求,求出临界粒径\(d_{\text{c}}\)
- 根据\(u_{\text{i}}\)和\(d_{\text{c}}\)计算旋风分离器的直径\(D\)
- 根据\(u_{\text{i}}\)与\(D\)计算旋风分离器的处理量,再根据气体流量确定旋风分离器的数目。
- 校核分离效率与压力降。
- 旋风分离器设计计算步骤:
第4章 传热
- 热传导:基本定律——傅里叶定律,\(\mathrm dQ = -\lambda \mathrm dA \cfrac {\partial t}{\partial n}\)。\(\lambda\)为导热系数,符号表示热流方向与温度梯度相反。
- 单层平壁的稳定热传导:\(Q = \lambda A\cfrac {t_1 - t_2}{b}\)。
- 多层平壁的稳定热传导:\(Q = \cfrac {t_1 - t_{n + 1}}{\sum_{i = 1}^{n} \cfrac {b_i}{\lambda_i A}}\)。
- 单层圆筒壁的热传导:\(Q = \cfrac {2\pi l\lambda(t_1 - t_2)}{\ln \cfrac {r_2}{r_1}}\)。
- 多层圆筒壁的热传导:\(Q = \cfrac {t_1 - t_4}{\cfrac {\ln \cfrac {r_2}{r_1}}{2\pi l \lambda_1} + \cfrac {\ln \cfrac {r_3}{r_2}}{2\pi l \lambda_2} + \cfrac {\ln \cfrac {r_3}{r_2}}{2\pi l \lambda_3}}\)。
- 对流传热:牛顿冷却定律,\(\mathrm dQ = \cfrac {T - T_{\text{w}}}{\cfrac {1}{\alpha \mathrm dS}} = \alpha(T - T_{\text{w}})\mathrm dS\)。
- 局部对流传热系数\(\alpha = \cfrac {Q}{S\Delta t}\)。
- \(Q = \cfrac {t_1 - t_\text{f}}{R_1 + R_2} = \cfrac {t_1 - t_{\text{f}}}{\cfrac {1}{2\pi L\lambda}\ln\cfrac{r_{\text{o}}}{r_{\text{i}}} + \cfrac {1}{2\pi Lr_{\text{o}\alpha}}}\)。
- 传热过程计算:
- \(Q = W_{\text{h}}(H_{\text{h}1} - H_{\text{h}2}) = W_{\text{c}}(H_{\text{c}1} - H_{\text{c}2})\)。
- \(Q = W_{\text{h}}c_{p\text{h}}(T_1 - T_2) = W_{\text{c}}c_{p\text{c}}(t_2 - t_1)\)。
- \(Q = K_{\text{o}}S_{\text{o}}\Delta t_{\text{m}}\),\(\Delta t_{\text{m}} = \cfrac {\Delta t_2 - \Delta t_1}{\ln \cfrac {\Delta t_2}{\Delta t_1}}\)。
- 对流传热系数关系式:量纲分析法,\(\alpha = f(l, \rho, \mu, c_{\text{p}}, \lambda, u)\)。
- 辐射传热:黑体、镜体、透热体和灰体(绝对黑体)。
- 普朗克定律:单色辐射能力。
- 斯蒂芬-玻尔兹曼定律:黑体辐射能力仅与热力学温度的四次方成正比,\(E_{\text{b}} = \sigma_0T^4 = C_0\left(\cfrac{T}{100}\right)^4\)。
- 克希霍夫定律:一切物体的发射能力与其吸收率的比值均相等,且等于同温度下的绝对黑体的发射能力,其值只与温度有关。\(\cfrac {E}{A} = \cfrac {E_1}{A_1} = \cdots = E_{\text{b}} = f(T)\)。
历次作业
第1次作业
2
所有螺钉所承受的压力与储油罐孔盖处的压力相等,将所需的螺钉数目记作\(n\),则有:
\[n \pi \left(\cfrac {14}{2}\right)^2 \times 32.23\times10^{6} = 960 \times (9.6 - 0.8) \times 9.81 \pi \left(\cfrac {760}{2}\right)^2\]求得:
\[n = \cfrac {960 \times 8.8 \times 9.81 \times 760^2}{14^2 \times 3.223 \times 10^7} = 7.58\]上取整,即至少需要8个螺钉。
3
\[p_{A} = \rho_{\text{水}}gR_3 + \rho_{\text{汞}}gR_2 = \pu{(1000 \times 9.81 \times 0.05 + 13600 \times 9.81 \times 0.05) Pa} = \pu{7.16E3 Pa}\text{(表压)}\] \[p_{B} = p_{A} + \rho_{\text{汞}}gR_1 = \pu{(7.16E3 + 13600 \times 9.81 \times 0.4) Pa} = \pu{6.05E4 Pa}\text{(表压)}\]4
\[\rho_{\text{煤油}}gh + \rho_{\text{水}}g(H - h) = \rho_{\text{汞}}gR\]故:
\[h = \cfrac {\rho_{\text{水}}gH - \rho_{汞}gR} {\rho_{\text{水}} - \rho_{\text{煤油}}} = \pu{\cfrac {1000 \times 9.81 \times 1 - 13600 \times 9.81 \times 0.068}{10000 - 820} m} = \pu{0.418 m}\]6
由于扩大室内径和U型管内径已知,故右侧液面比左侧液面高出:
\[h = \cfrac {R \times d^2}{D^2} = \pu{3 mm}\]故:
\[p = (\rho_{\text{水}} - \rho_{\text{油}})gR + \rho_{\text{油}}gh = \pu{((998 - 920) \times 9.81 \times 0.3 + 920 \times 9.81 \times 0.003) Pa} = \pu{2.57E2 Pa}\]第2次作业
8
(1) 由伯努利方程,有:
\[gZ_1 + \cfrac {u_1^2}{2} + \cfrac {p_1}{\rho} + W_{\text{e}} = gZ_2 + \cfrac {u_2^2}{2} + \cfrac {p_2}{\rho} + \sum h_{\text{f}}\]水槽截面较大,故水槽内的流速\(u_1 \approx 0\);水面与大气接触,表压均为大气压;故:
\[g(Z_1 - Z_2) = \cfrac {u^2}{2} + 6.5 u^2 = 7u^2\]即:
\[u = \sqrt{\cfrac {9.81 \times (8 - 2)}{7}}~\pu{m/s} = \pu{2.90 m/s}\](2) 由已知:
\[V_{\text{s}} = \cfrac {\pi}{4}ud^2 = \cfrac {\pi}{4}\times 2.90 \times 3600 \times 0.1^2~\pu{s}= \pu{82.0 m3/h}\]10
水槽截面较大,其流速视为0。研究水槽表面到取水口的过程:
\[0 = gZ_1 + \cfrac {u^2}{2} + \cfrac {p_1}{\rho} + \sum h_{\text{f}, 1}\]求得:
\[u = \sqrt{\cfrac{9.81 \times 1.5 + 24.66}{2.5}}~\pu{m/s} = \pu{2.0 m/s}\]研究取水口到排水口的过程:
\[gZ_1 + \cfrac {u^2}{2} + \cfrac {p_1}{\rho} + W_{\text{e}} = gZ_2 + \cfrac {u^2}{2} + \cfrac {p_2}{\rho} + \sum h_{\text{f}, 2}\]求得:
\[\begin{align}W_{\text{e}} &= g(Z_2 - Z_1) + \cfrac {p_2 - p_1}{\rho} + \sum h_{\text{f}, 2} \\ &= [9.81 \times 12.5 + (98.07 + 24.66) + 10 \times 2.0^2]~\pu{J/s} \\ &= \pu{285.4 J/kg}\end{align}\]质量流量为:
\[w_{\text{e}} = \cfrac {\pi}{4}u\rho d^2 = \left[\cfrac {\pi}{4} \times 2.0 \times 10^3 \times (0.076 - 0.0025)^2\right]~\pu{kg/s} = \pu{7.9 kg/s}\]故功率为:
\[W = W_{\text{e}}w_{\text{e}} = (285.4 \times 7.9)~\pu{W} = \pu{2.25 kW}\]12
(1) 研究A → A的过程:
\[W_{\text{e}} = \sum h_{\text{f}, AB} + \sum h_{\text{f}, BA} = (98.1 + 49)~\pu{J/kg} = \pu{147.1 J/kg}\]质量流量为:
\[w_{\text{e}} = V_{\text{e}}\rho = \cfrac {36 \times 1100}{3600}~\pu{kg/s} = \pu{11 kg/s}\]故有效功率为:
\[W = W_{\text{e}}w_{\text{e}} = (147.1 \times 11)~\pu{W} = \pu{1.62 kW}\]轴功率为:
\[W' = W/\eta = \pu{2.31 kW}\](2) 研究A → B的过程:
\[\cfrac {p_A}{\rho} = gZ_B + \cfrac {p_B}{\rho} + \sum h_{\text{f}, AB}\]求得:
\[\begin{align}p_B &= p_A - \rho(\sum h_{\text{f}, AB} + gZ_B) \\ &= [245.2 \times 10^3 - 1100 \times (49 + 9.81 \times 7)]~\pu{Pa} \\ &W= \pu{6.2E4 Pa}(\text{表压})\end{align}\]13
(1) 对AD段列伯努利方程,有:
\[\cfrac {p_1}{\rho} = gZ_D + \sum h_{\text{f}} \tag{1}\]对BC段列流体静力学方程,有:
\[p_B + \rho gR_1 = p_C + \rho g(Z_C - Z_B) + \rho_{\text{汞}}gR_1\]即:
\[p_B - p_C = \rho g(Z_C - Z_B) + (\rho_{\text{汞}} - \rho)gR_1 \tag{2}\]列伯努利方程,有:
\[gZ_B + \cfrac {p_B}{\rho} = gZ_C + \cfrac {p_C}{\rho} + \sum h_{\text{f}, BC} \tag{3}\]联立(2)(3)得到:
\[1.18u^2 = \sum h_{\text{f}, BC} = \cfrac {(\rho_{\text{汞}} - \rho)gR_1}{\rho}\]即:
\[u = \sqrt{\cfrac {(\rho_{\text{汞}} - \rho)gR_1}{1.18\rho}} = \sqrt{\cfrac {(13600 - 1100)\times 9.81 \times 0.045}{1.18 \times 1100}}~\pu{m/s} = \pu{2.1 m/s}\]代入(1)得:
\[\begin{align}p_1 &= \rho(gZ_D + 3.18u^2) \\ &= 1100 \times (9.81 \times 10 + 3.18 \times 2.1^2)~\pu{Pa} \\ &= \pu{1.23E5 Pa}(\text{表压})\end{align}\](2) 由流体静力学方程,有:
\[p_B + \cfrac {u^2}{2} = \rho_{\text{汞}}gR_2 + \rho gh \tag{4}\]对BD段列伯努利方程,有:
\[gZ_B + \cfrac {p_B}{\rho} = gZ_D + \sum h_{\text{f}, BC} + \sum h_{\text{f}, CD} \tag{5}\]联立(4)(5)得到:
\[\begin{align}R_2 &= \cfrac {\rho[g(Z_D - Z_B) + 1.68u^2] - \rho gh}{\rho_{\text{汞}}g} \\ &= \cfrac {1100 [9.81 \times 7 + 1.68 \times 2.1^2] - 1100 \times 9.81 \times 0.2}{13600 \times 9.81}~\pu{m} \\ &= \pu{611 mm} \end{align}\]第3次作业
2
查65 ℃下水的饱和蒸气压,\(p_{\text{v}} = \pu{2.554E4 Pa}\),\(\rho = \pu{980.5 kg/m3}\)。
对水面到喷头处的过程,有:
\[\cfrac {p_1}{\rho g} + H = \cfrac {p_2}{\rho g} + H_{\text{f}} + Z\]求得:
\[H = \left( \cfrac {49 \times 10^3}{980.5 \times 9.81} + 1 + 5 + 8 \right)~\pu{m} = \pu{19.1 m}\]查图2-28,选用型号为IS80-65-125的泵。
查附录20,\((NPSH)_{\text{r}} = \pu{3.0 m}\)。
\[\begin{align}H_{\text{g}} &= \cfrac {p_0 - p_{\text{v}}}{\rho g} - (NPSH)_{\text{r}} - H_{\text{f}} \\ &= \left(\cfrac {101.33 \times 10^3 - 2.554 \times 10^4}{980.5 \times 9.81} - 3 - 1\right)~\pu{m} \\ &= \pu{3.9 m}\end{align}\]3
查得65Y-60B型泵流量为\(Q = \pu{19.8 m3/s}\),气蚀余量\(\Delta h = \pu{2.6 m}\),扬程\(H = \pu{38 m}\)。
\[H_{\text{g}} = \cfrac {p_0 - p_{\text{v}}}{\rho g} - H_{\text{f}} = \pu{-0.74 m} > \pu{-1.2 m}\] \[Z = H - H_{f, 0-2} = (38 - 4)~\pu{m} = \pu{34 m}\] \[\cfrac {p_1}{\rho g} + H = \cfrac {p_2}{\rho g} + H_{f, 1-2} + \Delta Z\]则:
\[\begin{align}H_{\text{e}} &= \cfrac {p_2 - p_1}{\rho g} + H_{f, 1-2} + \Delta Z \\ &= \left( \cfrac {177 \times 10^3}{760 \times 9.81} + 5 + 5 \right)~\pu{m} \\ &= \pu{33.7 m} < \pu{34 m}\end{align}\] \[Q_{\text{e}} = \pu{15 m3/s} < \pu{19.8 m3/s}\]故能正常操作。
7
(1)
\[H_{\text{e}} = K + BQ^2\] \[K = \Delta Z + \cfrac {\Delta p}{\rho g}\]由题设吸入、排出空间均为常压设备,\(\Delta p = 0\),即\(K = \Delta Z = \pu{4.8 m}\)。
\[\begin{align}B &= \lambda \cfrac {l + \sum l_{\text{e}}} {d} \cfrac {1} {2g (60 \times 10^3 A)^2} \\ &= 0.03 \times \cfrac {355}{0.068} \times \cfrac {1}{2 \times 9.81 \times \left(60 \times 10^3 \times \pi \times \frac {0.068^2}{4}\right)^2}~\pu{min2/L2} \\ &= \pu{1.68E-4 min2/L2} \end{align}\]绘制:
\[H_{\text{e}} = 4.8 + 1.68 \times 10^{-4}Q^2\]并绘出\(H-Q\)曲线,得:
由图可知,泵的流量为\(\pu{400 L/min}\)。
(2)
代入\(\Delta p = \pu{1.295E5 Pa}\),得\(K = \pu{18.0 m}\)。
绘入上图,泵的流量为\(\pu{310 L/min}\)。
8
若为串联,\(H_{\text{e}} = 2H\),即:
\[10 + 1 \times 10^5 Q_{\text{e}}^2 = 2 \times (25 - 1 \times 10^6 Q^2)\]解得\(Q_{\text{e}} = \pu{4.36E-3 m3/s}\)。
若为并联,\(Q = Q_{\text{e}} / 2\),即:
\[10 + 1 \times 10^5 (2Q)^2 = 25 - 1 \times 10^6 Q^2\]解得\(Q = \pu{3.27E-3 m3/s}\),\(Q_{\text{e}} = \pu{6.55E-3 m3/s}\)。
故并联输液量大。
第4次作业
1. 取颗粒试样500 g,作筛分分析,所用筛号及筛孔尺寸见本题附表中第1、2列,筛析后称取各号筛面上的颗粒截留量列于本题附表中第3列,试求颗粒群的平均直径。
| 筛号 | 筛孔尺寸/mm | 截留量/g | 筛号 | 筛孔尺寸/mm | 截留量/g | |
|---|---|---|---|---|---|---|
| 10 | 1.651 | 0 | 65 | 0.208 | 60.0 | |
| 14 | 1.168 | 20.0 | 100 | 0.147 | 30.0 | |
| 20 | 0.833 | 40.0 | 150 | 0.104 | 15.0 | |
| 28 | 0.589 | 80.0 | 200 | 0.074 | 10.0 | |
| 35 | 0.417 | 130 | 270 | 0.053 | 5.0 | |
| 48 | 0.295 | 110 | 共计:500 | |||
计算筛分直径:
\[d_1 = \cfrac {d_{10} + d_{14}}{2} = \cfrac {1.651 + 1.168}{2}~\pu{mm} = \pu{1.410 mm}\]同理求出\(d_2\)~\(d_{10}\)为:1.001,0.711,0.503,0.356,0.252,0.178,0.126,0.089,0.064 mm。
由平均粒径公式:
\[\cfrac {1}{d_a} = \cfrac {1}{G} \sum \cfrac {G_i}{d} = \cfrac {1}{500} \left(\cfrac {20}{1.410} + \cdots + \cfrac {5}{0.064}\right) = \pu{2.905 mm-1}\]则平均粒径为:\(d_a = \cfrac {1}{2.905}~\pu{mm} = \pu{0.344 mm}\)。
2. 密度为2650 kg/m3的球形石英颗粒在20 ℃空气中自由沉降,计算服从斯托克斯公式的最大颗粒直径及服从牛顿公式的最小颗粒直径。
(1) 服从斯托克斯公式需要\(Re < 1\),即\(\cfrac {du_t\rho}{\mu} < 1\)。
其中\(u_t = \cfrac {d^2(\rho_{\text{s}} - \rho)g}{18 \mu}\),\(\rho = \pu{1.205 kg/m3}\),\(\mu = \pu{1.81E-5 Pa*s}\)。
故\(\cfrac {d^3\rho(\rho_{\text{s}} - \rho)g}{18\mu^2} < 1\),代入数值得:
\[d < \sqrt[3]{\cfrac {18\mu^2}{\rho(\rho_{\text{s}} - \rho)g}} = \pu{5.73E-5 m} = \pu{57.3 \mu m}\](2) 服从牛顿公式需要\(10^3 < Re < 2\times 10^5\)。
其中\(u_t = 1.74 \sqrt{\cfrac {d(\rho_{\text{s}} - \rho)g}{\rho}}\)。
故\(\cfrac {1.74d^{3/2}\sqrt{\rho(\rho_{\text{s} - \rho})g}}\mu{} > 10^3\),代入数值得:
\[d > \left(\cfrac {10^3\mu}{1.74\sqrt{\rho(\rho_{\text{s} - \rho})g}}\right)^{2/3} = \pu{1.51E-3 m} = \pu{1511 \mu m}\]3. 在底面积为40 m2的除尘室内回收气体中的球形固体颗粒。气体的处理量为3600 m3/h,固体的密度ρs = 3000 kg/m3,在操作条件下气体的密度ρ = 1.06 kg/m3,黏度为2 × 10-5 Pa·s。试求理论上能完全除去的最小颗粒直径。
计算沉降速率:
\[u_t = \cfrac {V}{b} = \cfrac {3600}{40}~\pu{m/h} = \pu{0.025 m/s}\]假设颗粒物符合斯托克斯公式,\(Re < 1\),则:
\[u_t = \cfrac {d^2(\rho_{\text{s}} - \rho)}{18 \mu}\]即:
\[d = \sqrt{\cfrac {18 \mu u_t}{(\rho_{\text{s}} - \rho)g}} = \pu{1.75E-5 m} = \pu{17.5 \mu m}\]代入计算\(Re = \cfrac {du_t\rho}{\mu} < 1\),符合假设。
5. 已知含尘气体中尘粒的密度为2300 kg/m3,气体流量为1000 m3/h、黏度为3.6 × 10-5 Pa·s、密度为0.674 kg/m3,采用如图3-7所示的标准型旋风分离器进行除尘。若分离器圆筒直径为0.4 m,试估算其临界粒径、分割粒径及压力降。
选用的标准型旋风分离器\(N_{\text{e}} = 5\),\(\zeta = 8.0\),\(B = D/4\),\(h = D/2\)。
由\(V_{\text{s}} = Bhu_{\text{i}}\)得:
\[u_{\text{i}} = \cfrac {8V}{D^2} = \cfrac {8 \times 1000}{0.4^2}~\pu{m/h} = \pu{50000 m/h} = \pu{13.89 m/s}\]临界直径为:
\[d = \sqrt{\cfrac {9\mu B}{\pi N_{\text{e}}\rho_{\text{s}}u_{\text{i}}}} = \sqrt{\cfrac {9 \times 3.6 \times 10^{-5} \times 0.1}{\pi \times 5 \times 12 N \times 13.89}}~\pu{m} = \pu{8.04 \mu m}\]分割粒径为:
\[d_{50} = 0.27\sqrt{\cfrac {\mu D}{u_t(\rho_{\text{s}} - \rho)}} = 0.27\sqrt{\cfrac {3.6 \times 10^{-5} \times 0.4}{13.89(2300 - 0.674)}}~\pu{m} = \pu{5.73 \mu m}\]压强降为:
\[\Delta p = \zeta\rho\cfrac {u_{\text{i}}^2}{2} = 8.0 \times 0.674 \times \cfrac {13.89^2}{2}~\pu{Pa} = \pu{520 Pa}\]第5次作业
1. 平壁炉的炉壁由三种材料组成,其厚度和导热系数列于本题附表中。若耐火砖层内表面的温度t1为1150 ℃,钢板外表面温度t4为30 ℃,又测得炉壁的热损失为300 W/m2,试计算导热的热通量。若计算结果与实测的热损失不符,试分析原因和计算附加热阻。
| 序号 | 材料 | 厚度b/mm | 导热系数λ/W·m-1·℃ |
|---|---|---|---|
| 1(内层) | 耐火砖 | 200 | 1.07 |
| 2 | 绝缘砖 | 100 | 0.14 |
| 3 | 钢 | 6 | 45 |
根据多层平壁热传导速率公式,有:
\[Q = \cfrac {\Delta t_1 + \Delta t_2 + \Delta t_3}{\cfrac {b_1}{\lambda_1S_{m1}} + \cfrac {b_2}{\lambda_2S_{m2}} + \cfrac {b_3}{\lambda_3S_{m3}}} = \cfrac{t_1- t_4}{\cfrac {1}{S} \left(\cfrac {b_1}{\lambda_1} + \cfrac {b_2}{\lambda_2} + \cfrac {b_3}{\lambda_3}\right)}\] \[q = \cfrac {Q}{S} = \cfrac {1150 - 30}{\cfrac {0.2}{1.07} + \cfrac{0.1}{0.14} + \cfrac {0.006}{45}}~\pu{W/m2} = \pu{1142 W/m2}\]与实测热损失\(q = \pu{300 W/m2}\)有差距,故认为存在附加热阻,即:
\[q' = \cfrac {\Delta t_1 + \Delta t_2 + \Delta t_3}{\cfrac {b_1}{\lambda_1S_{m1}} + \cfrac {b_2}{\lambda_2S_{m2}} + \cfrac {b_3}{\lambda_3S_{m3}} + R} = \pu{300 W/m2}\] \[R = \cfrac {t_1 - t_4}{q'} - \cfrac {b_1}{\lambda_1} - \cfrac {b_2}{\lambda_2} - \cfrac {b_3}{\lambda_3} = \pu{2.83 m2*^\circ C/W}\]2. 燃烧炉的内层为460 mm厚的耐火砖,外层为230 mm厚的绝缘砖。若炉的内表面温度t1为1400 ℃,外表面温度t3为100 ℃。试求导热的热通量及两砖间的界面温度。设两层砖接触良好,已知耐火砖的导热系数为λ1 = 0.9 + 0.0007t,绝缘砖的导热系数为λ2 = 0.3 + 0.0003t。两式中t可分别取为各层材料的平均温度,单位为℃,λ的单位为W/(m·℃)。
设界面温度为\(t_2\),热通量为\(q\),则:
\[\lambda_1 = 0.9 + 0.0007 \cfrac {t_1 + t_2}{2} = 1.39 + 0.00035 t_2\] \[\lambda_2 = 0.3 + 0.0003 \cfrac {t_2 + t_3}{2} = 0.315 + 0.00015 t_2\]有:
\[\cfrac {t_1 - t_2}{\cfrac {b_1}{\lambda_1}} = \cfrac {t_2 - t_3}{\cfrac {b_2}{\lambda_2}}~\text{即}~\cfrac {1400 - t_2}{\cfrac {0.46}{\lambda_1}} = \cfrac {t_2 - 100}{\cfrac {0.2}{\lambda_2}}\]解得\(t_2 = \pu{949 ^\circ C}\)。
则:
\[q = \cfrac {t_1 - t_3}{\cfrac {b_1}{\lambda_1} + \cfrac {b_2}{\lambda_2}} = \cfrac {1400 - 100}{\cfrac {0.46}{\lambda_1} + \cfrac {0.2}{\lambda_2}} = \pu{1689 W/m2}\]3. 直径为Φ60 mm × 3 mm的钢管用30 mm厚的软木包扎,其外又用100 mm厚的保温灰包扎,以作为绝热层。现测得钢管外壁面温度为-110 ℃,绝热层外表面温度为10 ℃。已知软木和保温灰的导热系数分别为0.043和0.07 W/(m·℃),试求每米管长的冷量损失量。
根据多层平壁热传导速率公式,有:
\[Q = \cfrac {t_1 - t_3}{\cfrac {1}{S_m}\left(\cfrac {b_1}{\lambda_1} + \cfrac {b_2}{\lambda_2}\right)} = \cfrac {2\pi L(t_1 - t_3)}{\cfrac {1}{\lambda_1}\ln \cfrac {r_2}{r_1} + \cfrac {1}{\lambda_2} \ln \cfrac {r_3}{r_2}}\]则:
\[\cfrac {Q}{L} = \cfrac {2\pi(-110 - 10)}{\cfrac {1}{0.043}\ln \cfrac {60}{30} + \cfrac {1}{0.07} \ln \cfrac {160}{60}}~\pu{W/m} = \pu{-25 W/m}\]5. 在外径为140 mm的蒸汽管道外包扎一层厚度为50 mm的保温层,以减少热损失。蒸汽管外壁温度为180 ℃。保温层材料的导热系数λ与温度t的关系为λ = 0.1 + 0.0002t(t的单位为℃,λ的单位为W/(m·℃))。若要求每米管长热损失造成的蒸汽冷凝量控制在9.86 × 10-5 kg/(m·s),试求保温层外侧面温度。
查附录,180 ℃下饱和水蒸气的汽化热为2019.3 kJ/kg。则热损失为:
\[\cfrac {Q}{L} = 9.86 \times 10^{-5} \times 2019.3 \times 10^3~\pu{W/(m*s)} = \pu{199.1 W/(m*s)}\]由热传导速率公式:
\[\cfrac {Q}{L} = \cfrac {2\pi(t_2 - t_3)}{\cfrac {1}{\lambda_2}\ln \cfrac {r_3}{r_2}}\]其中\(\lambda_2 = 0.1 + 0.0002 \cfrac {t_2 + t_3}{2} = 0.118 + 0.001 t_3\),则:
\[t_3 = t_2 - \cfrac {Q}{L}\cfrac {1}{\lambda_2}\ln\cfrac{r_3}{r_2} \cfrac {1}{2\pi} = \pu{40^\circ C}\]6. 在管壳式换热器中用冷水冷却油。水在直径为Φ19 mm × 2 mm的列管内流动。已知管内水侧对流传热系数为3490 W/(m·℃),管外油侧对流传热系数为258 W/(m·℃)。换热器在使用一段时间后,管壁两侧均有污垢形成,水侧污垢热阻为0.0026 (m·℃)/W,油侧污垢热阻为0.000176 (m·℃)/W。管壁导热系数λ为45 W/(m·℃)。试求:(1) 基于管外表面积的总传热系数;(2) 产生污垢后热阻增加的百分数。
(1) 由公式:
\[\begin{align}\cfrac {1}{K_0} &= \cfrac {1}{\alpha_0} + R_{\text{so}} + R_{\text{si}}\cfrac {d_{\text{o}}}{d_{\text{i}}} + \cfrac {d_{\text{o}}}{\alpha_{\text{i}}d_{\text{i}}} + \cfrac {bd_\text{o}}{\lambda d_\text{m}} \\ &= \cfrac {1}{258} + 0.000176 + 0.00026 \times \cfrac {19}{15} + \cfrac {19}{3490 \times 15} + \cfrac {0.002 \times 19}{16.9 \times 45} \\ &= \pu{0.00479 m2*^\circ C/W} \end{align}\]则\(K_0 = \pu{208 W/(m2*^\circ C)}\)。
(2) 产生污垢前的热阻为:
\[R_{\text{0}} = \cfrac {1}{\alpha_0} + \cfrac {d_{\text{o}}}{\alpha_{\text{i}}d_{\text{i}}} + \cfrac {bd_\text{o}}{\lambda d_\text{m}} = 0.00429\]则增加的百分比为:
\[\cfrac {R}{R_0} - 1 = \left(\cfrac {0.00479}{0.00429} - 1 \right)\times 100\% = 11.8\%\]第6次作业
8.重油和原油在单程套管换热器中呈并流流动,两种油的初温分别为243 ℃和128 ℃,终温分别为167 ℃和157 ℃。若维持两种油的流量和初温不变,而将两流体改为逆流,试求此时流体的平均温度差及它们的终温。假设在两种流动情况下,流体的物性和总传热系数均不变化,换热器的热损失可以忽略。
并流流动时,热流体\(\Delta T = T_1 - T_2 = (243 - 167)~\pu{^\circ C} = \pu{76 ^\circ C}\),冷流体\(\Delta t = t_2 - t_1 = (157 - 128)~\pu{^\circ C} = \pu{29 ^\circ C}\)。
\(\Delta t_1 = T_1 - t_1 = (243 - 128)~\pu{^\circ C} = \pu{115 ^\circ C}\),\(\Delta t_2 = T_2 - t_2 = (167 - 157)~\pu{^\circ C} = \pu{10 ^\circ C}\)。
\[\Delta t_{\text{m}} = \cfrac {\Delta t_1 - \Delta t_2}{\ln \cfrac {\Delta t_1}{\Delta t_2}} = \cfrac {115 - 10}{\ln \cfrac {115}{10}~\pu{^\circ C}} = \pu{43 ^\circ C}\] \[\begin{align}Q &= W_{\text{h}}c_{p\text{h}}(T_1 - T_2) = 76W_{\text{h}}c_{p\text{h}} \\ &= W_{\text{c}}c_{p\text{c}}(t_2 - t_1) = 29W_{\text{c}}c_{p\text{c}} \\ &= K_{\text{o}}S_{\text{o}}\Delta t_{\text{m}}\end{align}\]改为逆流流动后,热流体\(\Delta T = T_1 - T_2 = 243 - T_2\),冷流体\(\Delta t = t_2 - t_1 = t_2 - 128\)。
\(\Delta t_1 = T_1 - t_2 = 243 - t_2\),\(\Delta t_2 = T_2 - t_1 = T_2 - 128\)。
\[Q' = W_{\text{h}}c_{p\text{h}}(243 - t_2) = W_{\text{c}}c_{p\text{c}}(T_2 - 128)\]其中,\(\cfrac {W_{\text{h}}c_{p\text{h}}}{W_{\text{c}}c_{p\text{c}}} = \cfrac {29}{76}\),即:
\[\cfrac {243 - t_2}{T_2 - 128} = \cfrac {29}{76} \tag{1}\] \[\Delta t_{\text{m}}' = \cfrac {\Delta t_1 - \Delta t_2}{\ln \cfrac {\Delta t_1}{\Delta t_2}} = \cfrac {(243 - t_2) - (T_2 - 128)}{\ln \cfrac {243 - t_2}{T_2 - 128}} \tag{2}\] \[Q' = K_{\text{o}}S_{\text{o}}\Delta t_{\text{m}}' = \cfrac {243 - T_2}{76} Q\] \[\cfrac {\Delta t_{\text{m}}'}{\Delta t_{\text{m}}} = \cfrac {243 - T_2}{76} \tag{3}\]联立(1)(2)(3)得:\(T_2' = \pu{155.4 ^\circ C}\),\(t_2' = \pu{161.4 ^\circ C}\),\(\Delta t_{\text{m}}' = \pu{49.7 ^\circ C}\)。
9. 在下列各种管壳式换热器中,某种溶液在管内流动并由20 ℃加热到50 ℃。加热介质在壳方流动,其进、出口温度分别为100 ℃和60 ℃,试求下面各种情况下的平均温度差:(1) 壳方和管方均为单程的换热器,设两流体呈逆流流动;(2) 壳方和管方分别为单程和四程的换热器;(3) 壳方和官方分别为二程和四程的换热器。
(1) \(\Delta t_1 = (100 - 50)\pu{^\circ C} = \pu{50 ^\circ C}\),\(\Delta t_2 = (60 - 20)\pu{^\circ C} = \pu{40 ^\circ C}\)。
\[\Delta t_{\text{m}} = \cfrac {\Delta t_1 - \Delta t_2}{\ln \cfrac {\Delta t_1}{\Delta t_2}} = \pu{44.8 ^\circ C}\](2) 由已知计算
\[P = \cfrac {t_2 - t_1}{T_1 - t_1} = \cfrac {50 - 20}{100 - 20} = \cfrac {3}{8}\] \[R = \cfrac {T_1 - T_2}{t_2 - t_1} = \cfrac {100 - 60}{50 - 20} = \cfrac {4}{3}\]查图得\(\varphi_{\Delta t} = 0.9\),则\(\Delta t_{\text{m}}' = \Delta t_{\text{m}}\varphi_{\Delta t} = \pu{40.3 ^\circ C}\)。
(3) 查图得\(\varphi_{\Delta t} = 0.98\),则\(\Delta t_{\text{m}}' = \Delta t_{\text{m}}\varphi_{\Delta t} = \pu{43.9 ^\circ C}\)。
10. 在逆流换热器中,用初温为20 ℃的水将1.25 kg/s的液体(比热容为1.9 kJ/(kg·℃)、密度为850 kg/m3)由80 ℃冷却到30 ℃。换热器的列管直径为Φ25 mm × 2.5 mm,水走管方。水侧和液体侧的对流传热系数分别为0.85 kW/(m2·℃)和1.70 kW/(m2·℃),污垢热阻可忽略。若水的出口温度不能高于50 ℃,试求换热器的传热面积。
\[\Delta t_{\text{m}} = \cfrac {\Delta t_1 - \Delta t_2}{\ln \cfrac {\Delta t_1}{\Delta t_2}} = \cfrac {(80 - 50) - (30 - 20)}{\ln \cfrac {80 - 50}{30 - 20}}~\pu{^\circ C} = \pu{18.2 ^\circ C}\] \[Q = W_{\text{h}}c_{p\text{h}}(T_1 - T_2) = 1.25 \times 1.9 \times (80 - 30)~\pu{kW} = \pu{118.75 kW}\]不计污垢热阻,则\(\cfrac {1}{K_{\text{o}}} = \cfrac {1}{\alpha_{\text{o}}} + \cfrac {d_{\text{o}}}{\alpha_{\text{i}}d_{\text{i}}}\),即\(K_{\text{o}} = \pu{0.486 kW/(m2*^\circ C)}\)。
又因为\(Q = K_{\text{o}}S_{\text{o}}\Delta t_{\text{m}}\),故:
\[S_{\text{o}} = \cfrac {Q}{K_{\text{o}}\Delta t_{\text{m}}} = \cfrac {118.75}{0.486 \times 18.2}~\pu{m2} = \pu{13.9 m2}\]12. 在一传热面积为50 m2的单程管壳式换热器中,用水冷却某种溶液。两流体呈逆流流动。冷水的流量为33000 kg/h,温度由20 ℃升至38 ℃。溶液的温度由110 ℃降至60 ℃。若换热器清洗后,在两流体的流量和进口温度不变的情况下,冷水出口温度增到45 ℃。试估算换热器清洗前传热面两侧的总污垢热阻。假设:(1) 两种情况下,流体物性可视为不变,水的平均比热容可取4.187 kJ/(kg·℃);(2) 可按平壁处理,两种工况下αi和αo分别相同;(3) 忽略管壁热阻和热损失。
\[\Delta t_{\text{m}} = \cfrac {\Delta t_1 - \Delta t_2}{\ln \cfrac {\Delta t_1}{\Delta t_2}} = \cfrac {(110 - 38) - (60 - 20)}{\ln \cfrac {110 - 38}{60 - 20}}~\pu{^\circ C} = \pu{54.4 ^\circ C}\] \[\begin{align}Q &= W_{\text{h}}c_{p\text{h}}(T_1 - T_2) = 50W_{\text{h}}c_{p\text{h}} \\ &= W_{\text{c}}c_{p\text{c}}(t_2 - t_1) = 18W_{\text{c}}c_{p\text{c}} = \left(18 \times \cfrac {3.3 \times 10^4}{3600} \times 4.187 \times 10^3\right)~\pu{W} = \pu{6.9E5 W} \\ &= K_{\text{o}}S_{\text{o}}\Delta t_{\text{m}}\end{align}\]则:
\[K_{\text{o}} = \cfrac {Q}{S_{\text{o}}\Delta t_{\text{m}}} = \cfrac {6.9\times 10^5}{50 \times 54.4}~\pu{W/(m2*^\circ C)} = \pu{253.8 W/(m2*^\circ C)}\]清洗后,\(\Delta t_1 = (110 - 45)~\pu{^\circ C} = \pu{65^\circ C}\),\(\Delta t_2 = T_2 - 20\)。
\[\Delta t_{\text{m}}' = \cfrac {65 - (T_2 - 20)}{\ln \cfrac {65}{T_2 - 20}}~\pu{^\circ C} \tag{1}\] \[\begin{align}Q' &= (110 - T_2)W_{\text{h}}c_{p\text{h}} \\ &= 25W_{\text{c}}c_{p\text{c}} = \pu{9.6E5 W} \\ &= K_{\text{o}}'S_{\text{o}}\Delta t_{\text{m}}'\end{align} \tag{2}\]联立(1)(2)得\(T_w = \pu{40.6 ^\circ C}\),\(\Delta t_{\text{m}}' = \pu{38.6^\circ C}\),\(K_{\text{o}}' = \pu{497.1 W/(m2*^\circ C)}\)。
故污垢热阻\(R = \cfrac {1}{K_{\text{o}}} - \cfrac {1}{K_{\text{o}}'} = \pu{1.93E-3 m2*^\circ C/W}\)。
第7次作业
20. 温度为90 ℃的甲苯以1500 kg/h的流量通过蛇管而被冷却至30 ℃。蛇管的直径为Φ57 mm × 3.5 mm,弯管半径为0.6 m,试求甲苯对蛇管壁的对流传热系数。
查甲苯在60 ℃下的物性常数,\(\mu = \pu{0.375E-3 Pa*s}\),\(\lambda = \pu{0.143 W/(m2*^\circ C)}\),\(\rho = \pu{830 kg/m3}\),\(c_p = \pu{1.8376E3 J/(kg*^\circ C)}\)。
\[Re = \cfrac {du\rho}{\mu} = \cfrac {dQ}{Au} = \cfrac {0.05 \times \cfrac {1500}{3600}}{\cfrac {\pi}{4} \times 0.05^2 \times 0.375 \times 10^{-3}} = 2.83\times 10^4 > 10^4\]按湍流计算。
\[Pr = \cfrac {c_p \mu}{\lambda} = \cfrac {1.8376\times 10^3 \times 0.375 \times 10^-3}{0.143} = 4.82\] \[\alpha = 0.023\cfrac {\lambda}{d_i}Re^{0.8}Pr^{n}\]冷却时,\(n\)取0.3。故:
\[\alpha = 0.23 \times \cfrac {0.143}{0.05}\times (2.83 \times 10^4)^{0.8}\times 4.82^{0.3}~\pu{W/(m2*^\circ C)} = \pu{384 W/(m2*^\circ C)}\] \[\alpha' = \alpha\left(1 + 1.77 \cfrac {d_i}{r}\right) = 384 \times\left(1 + 1.77 \cfrac {0.05}{0.6}\right)~\pu{W/(m2*^\circ C)} = \pu{441 W/(m2*^\circ C)}\]25. 两平行的大平板放置在空气中,相距5 mm。一平板的黑度为0.1,温度为350 K;另一平板的黑度为0.05,温度为300 K。若将第一板加涂层,使其黑度变为0.025,试计算由此引起的传热量变化的百分率。假设两板间对流传热可以忽略。
传热量分为空气热传导和板间热辐射。考虑空气热传导,查空气传热系数\(\lambda = \pu{0.282 W/(m2*^\circ C)}\),则:
\[q = \cfrac{\lambda \Delta t}{b} = \cfrac{0.282 \times (350 - 300)}{5 \times 10^{-3}}~\pu{W/m2} = \pu{282 W/m2}\]改变前板间热辐射为:
\[C_1 = \cfrac{C_0}{\cfrac{1}{\varepsilon_1} + \cfrac{1}{\varepsilon_2} - 1} = \cfrac {5.67}{10 + 20 - 1}~\pu{W/(m2*K4)} = \pu{0.1955 W/(m2*K4)}\] \[q_1 = C_1\left[\left(\cfrac{T_1}{100}\right)^4 - \left(\cfrac{T_2}{100}\right)^4\right] = 0.1955 \times(3.5^4 - 3^4)~\pu{W/m2} = \pu{13.5 W/m2}\]改变后板间热辐射为:
\[C_2 = \cfrac{C_0}{\cfrac{1}{\varepsilon_1'} + \cfrac{1}{\varepsilon_2} - 1} = \cfrac {5.67}{40 + 20 - 1}~\pu{W/(m2*K4)} = \pu{0.096 W/(m2*K4)}\] \[q_2 = C_2\left[\left(\cfrac{T_1}{100}\right)^4 - \left(\cfrac{T_2}{100}\right)^4\right] = 0.096 \times(3.5^4 - 3^4)~\pu{W/m2} = \pu{6.63 W/m2}\]则改变的比率为:
\[\cfrac {q_2 - q_1}{q_1 + q} = \cfrac {6.63 - 13.5}{13.5 + 282} \times 100\% = -2.3\%\]26. 在管道中心装有热电偶以测量管内空气的温度。由于气体真实温度t1与管壁温度tw不相同,故测温元件与管壁间的辐射传热引起测量误差。试推导出计算测温误差(t1 - t1*)的关系式。式中t1*为测量值。并说明降低测温误差的方法。假设热电偶的黑度为ε,空气与热电偶间的对流传热系数为α。
空气与热电偶间存在热传导:
\[Q_1 = \alpha S(t_1 - t^*)\]管壁与热电偶间存在热辐射:
\[Q_2 = C_{1-2}\varphi S\left[\left(\cfrac {t_w}{100}\right)^4 - \left(\cfrac {t_1^*}{100}\right)^4\right]\]其中,\(\varphi = 1\),\(C_{1-2} = C_0\varepsilon\)。
达到平衡时,\(Q_1 = Q_2\),即:
\[t_1 - t^* = \cfrac {C_0\varepsilon}{\alpha}\left[\left(\cfrac {t_w}{100}\right)^4 - \left(\cfrac {t_1^*}{100}\right)^4\right]\]可行方法:降低热电偶黑度、增大空气热对流常数。
思考题 7. 每小时有一定量的气体在套管换热器中从T1冷却到T2,冷水进、出口温度分别为t1和t2,两流体呈逆流流动,并均为湍流。若换热器尺寸已知,气体向管壁的对流传热系数比管壁向水的对流传热系数小得多,污垢热阻和管壁热阻均可以忽略不计。试讨论以下各项:(1) 若气体的生产能力加大10%,如仍用原换热器,但要维持原有的冷却程度和冷却水进口温度不变,试问应采取什么措施?并说明理由;(2) 若因气候变化,冷水进口温度下降至t1',现仍用原换热器并维持原冷却程度,则应采取什么措施?说明理由;(3) 在原换热器中,若将两流体改为并流流动,若要求维持原有的冷却成都和加热程度,是否可能?为什么?如不可能,试说明应采取什么措施?(设T2 > t2)
(1) 可以增大换热面积,增加冷却水流量。
(2) 可以减小换热面积,降低冷却水流量。
理由:对(1)(2)均有:
\[Q = C_{p\text{c}}W_{\text{c}}(t_2 - t_1)\]对(1),\(Q\)上升,且\(t_2 - t_1\)不变,则\(W_{\text{c}}\)上升。
对(2),\(Q\)不变,且\(t_2 - t_1\)升高,则\(W_{\text{c}}\)下降。
(3) 在逆流时:
\[\Delta t_{\text{m1}} = \cfrac {(T_1 - t_2) - (T_2 - t_1)}{\ln \cfrac {T_1 - t_2}{T_2 - t_1}}\]在并流时:
\[\Delta t_{\text{m2}} = \cfrac {(T_1 - t_1) - (T_1 - t_1)}{\ln \cfrac {T_1 - t_1}{T_1 - t_1}}\]计\(\Delta t_{\text{m}} = \cfrac {\Delta t_1 - \Delta t_2}{\ln \Delta t_1 - \ln \Delta t_2}\),则\(\cfrac {1}{\Delta t_{\text{m}}} = \cfrac {\ln \Delta t_1 - \ln \Delta t_2}{\Delta t_1 - \Delta t_2}\),为函数图像上两点斜率。
若\(\Delta t_{\text{m1}} = \Delta t_{\text{m2}}\),则有\(T_1 - t_2 = T_1 - t_1\),即\(t_1 = t_2\)显然不可能。
故不能维持原有冷却程度,且\(T_1 - t_2 < T_1 - t_1\),故需要增大换热面积或增加流量。

