第二章 燃烧与大气污染
2.1 燃料的性质
2.1.1 煤
- 煤是重要的固体燃料,可燃成分主要是由碳、氢以及少量氧、氮和硫等一起构成的有机聚合物。
- 煤的分类:
- 褐煤:最低品位的煤,形成年代最短,结构类似木材,热值较低。
- 烟煤:形成年代比褐煤长,成焦性较强,且含氧量低,水分和灰分含量不高,适宜工业上的一般应用,比褐煤更能抵抗风化。
- 无烟煤:碳含量最高,煤化时间最长,机械强度高,着火困难,成焦性极差。
- 煤的工业分析:
- 水分:包括外部和内部水分。
- 灰分:煤中不可燃矿物物质的总称。其存在降低煤的热值,增加了烟尘污染及出渣量。’
- 挥发分:煤在隔绝空气条件下加热分解出的可燃气态物质。
- 固定碳:从煤中扣除水分、灰分及挥发分后剩余的部分。是煤的主要可燃物质。
- 煤的元素分析:
- 碳和氢:碳是煤中有机质的主要组成元素,是发热量的主要来源。氢在煤中的重要性仅次于碳,与碳相比单位质量的燃烧热更大。通过测定燃烧尾气中 \(\ce{CO2}\) 和 \(\ce{H2O}\) 的生成量测定。
- 氧:氧在煤中的存在的总量和形态直接影响煤的性质。一般不直接测定,而是通过其他元素测定结果间接计算氧含量。
- 氮:氮是煤中唯一完全以有机状态存在的元素。通过催化剂作用转变为氨测定。
- 硫:硫对于炼焦、气化、燃烧和储运都十分有害,是评价煤质的重要指标之一。将样品放在 \(\ce{MgO}\) 和无水 \(\ce{Na2CO3}\) 的混合物上加热,使硫化物变为硫酸盐,再以重量法测定硫酸钡沉淀。
- 煤中硫的形态:
- 煤中主要还有四种形态的硫:黄铁矿硫(\(\ce{FeS2}\))、硫酸盐硫(\(\ce{MeSO4}\))、有机硫(\(\ce{C_xH_yS_z}\))和元素硫。
- 一般把硫分为硫化铁硫、有机硫和硫酸盐硫三种。前两种燃烧放出热量称为挥发硫,硫酸盐不参加燃烧,是灰分的一部分。
2.1.2 石油
- 石油是液体燃料的主要来源。原油是天然存在的易流动的液体,它是多种化合物的混合物。
- 原油通过蒸馏、裂化和重整生产出各种汽油、溶剂、化学产品和燃料油。
- 原油中的硫大部分以有机硫的形式存在,大多留于重馏分中。
2.1.3 天然气
- 天然气是典型的气体燃料,主要含甲烷、乙烷、丙烷等碳氢化合物。
- 天然气中的硫化氢具有腐蚀性。
2.1.4 非常规燃料
- 城市固体废弃物。
- 商业和工业固体废弃物。
- 农产品及农村废物。
- 水生植物和水生废物。
- 污泥处理厂废物。
- 可燃性工业和采矿废物。
- 天然存在的含碳和含碳氢的资源。
- 合成染料。
2.2 燃料燃烧过程
2.2.1 影响燃烧过程的主要因素
- 燃烧和燃烧产物:
- 燃烧:可燃混合物的快速氧化过程,并伴随着能量(光和热)的释放,同时使燃料的组成员组转化为相应的氧化物。
- 多数化石燃料的燃烧产物是二氧化碳和水蒸气,不完全燃烧产生黑烟、一氧化碳和其他部分氧化产物等大气污染物。
- 若燃料中含有硫和氮,则会生成 \(\ce{SO2}\) 和 \(\ce{NO}\)。
- 当燃烧室温度较高时空气中的部分氮会被氧化成 \(\ce{NO_x}\),称为热力型氮氧化物。
- 燃料完全燃烧的条件:
- 空气条件:燃料燃烧时必须保证供应与燃料燃烧相适应的空气量。空气供应不足燃烧不安全,供应量过大降低炉温增加损失。
- 温度条件:燃料只有达到着火温度,才能与氧作用燃烧。着火温度按固体燃料、液体燃料、气体燃料的顺序上升。
- 时间条件:燃料在燃烧室中的停留时间应超过燃料燃烧所需要的时间。
- 燃料与空气的混合条件:燃料和空气中氧的充分混合也是有效燃烧的基本条件。混合程度取决于空气的图按流毒。湍流可以加速也倜然俩的蒸发,有助于破坏燃烧产物在固体燃料表面形成的边界层。
- 通常把温度、时间和湍流称为燃烧过程的“3T”。
2.2.2 燃料燃烧的理论空气量
- 理论空气量:单位量燃料按燃烧放反应方程式完全燃烧所需要的空气量。
- 假定:
- 空气仅是由氮和氧组成的,其体积比为 \(79.1/20.9 = 3.78\)。
- 燃料中的固定态氧可用于燃烧。
- 燃料中的硫主要被氧化为 \(\ce{SO2}\)。
- 热力型 \(\ce{NO_x}\) 的生成量较小,燃料中含氮量也比较低,在计算理论空气量时可以忽略。
- 燃料中的氮在燃烧室转化为 \(\ce{N2}\) 和 \(\ce{NO}\),一般以 \(\ce{N2}\) 为主。
- 燃料的化学式为 \(\ce{C_xH_yS_zO_w}\)。
- 由此可得燃料与空气中氧完全燃烧的化学反应方程式:\(\ce{C_xH_yS_zO_w + (\mathit{x} + y/4 + \mathit{z} - w/2)O3 + 3.78(\mathit{x} + y/4 + \mathit{z} - w/2)N2 }\) \(\ce{-> xCO2 + y/2H2O + zSO2 + 3.78(\mathit{x} + y/4 + \mathit{z} - w/2)N2 + }Q\)。
- 理论空气量 \(V_{\mathrm a}^0 = \cfrac {22.4 \times 4.78\left(x + \cfrac y4 + z - \cfrac w2\right)}{12x + 1.008y + 32z + 16w}\)。
- 气体组成通常以摩尔分数表示,它不随气体温度和压力变化。
- 一般煤的理论空气量 \(4 \text{~} \pu{9 m3/kg}\),液体燃料 \(10 \text{~} \pu{11 m3/kg}\)。
- 空气过剩系数:在实际的燃烧装置中不可能达到理想化,为使燃料完全燃烧必须供给过量的空气。定义空气过剩系数 \(\alpha = \cfrac {V_{\mathrm a}}{V_{\mathrm a}^0}\),其中 \(V_{\mathrm a}\) 为实际空气量。通常 \(\alpha > 1\),取决于燃料种类、燃烧装置形式和燃烧条件等因素。
- 空燃比(AF):单位质量燃烧所需要的空气质量,可以直接由燃烧方程式求得。
2.2.3 燃烧产生的污染物
- 燃烧烟气主要由悬浮的少量颗粒物、燃烧产物、未燃烧和部分燃烧的燃料、氧化剂以及惰性气体(主要为 \(\ce{N2}\))等组成。
- 燃烧可能释放出的污染物有:\(\ce{CO2}\)、\(\ce{CO}\)、\(\ce{SO_x}\)、\(\ce{NO_x}\)、烟、飞灰、金属及其氧化物、金属盐类、醛、酮和稠环碳氢化合物等。
 图2-1 燃烧产物与温度的关系
图2-1 燃烧产物与温度的关系
2.2.4 热化学关系式
- 在充分混合的条件下,热量总损失在理论空气量条件下最低。
- 当混合不充分时,热量总损失的最小值出现在空气过量一侧。
2.3 烟气体积及污染物排放量计算
- 理论烟气体积 \(V_{\mathrm {fg}}^0\):在理论空气量下,燃料完全燃烧所生成的烟气体积。烟气成分主要是 \(\ce{CO2}\)、\(\ce{SO2}\)、\(\ce{N2}\) 和水蒸气。
- 干烟气:烟气中除了水蒸气以外的部分。湿烟气:包括水蒸气在内的烟气。理论烟气量 = 干烟气量 + 水蒸气体积。
- 实际烟气量 = 理论烟气量 + 过剩空气量。\(V_{\mathrm {fg}} = V_{\mathrm {fg}}^0 +(\alpha - 1)V_{\mathrm a}^0\)
- 烟气体积和密度的校正:\(V_{\mathrm N} = V_{\mathrm s}\cfrac{p_{\mathrm s}T_{\mathrm N}}{p_{\mathrm N}T_{\mathrm s}}\),其中 \(_{\mathrm N}\) 是标准状态 \(\pu{273 K}\)、\(\pu{101325 Pa}\),\(_{\mathrm s}\) 是观测状态。
- 过剩空气校正:
- 以碳在空气中的完全燃烧为例:\(\ce{C + O2 + 3.78N2 -> CO2 + 3.78N2}\),若空气过量则变为 \(\ce{C + (1+\mathit{a})O2 + 3.78(1+\mathit{a})N2 }\) \(\ce{-> CO2 + aO2 + 3.78(1+\mathit{a})N2}\)。
- 空气过剩系数:\(\alpha = \cfrac {V_{\mathrm a}}{V_{\mathrm a}^0} = 1 + a\)。
- 若燃烧完全,过剩空气中氧以 \(\ce{O2}\) 的形式存在,假如燃烧产物以下标 \(_{\mathrm p}\) 表示:\(\ce{C + (1+\mathit{a})O2 + 3.78(1+\mathit{a})N2 ->} \mathrm{CO_{2p} + O_{2p} + N_{2p}}\)。
- 假设空气体积组成为 \(20.9~\%~\ce{O2}\) 和 \(79.1~\%~\ce{N2}\),则实际空气中所含的总氧量为 \(\cfrac {20.9}{79.1}\varphi(\mathrm{N_{2p}}) = 0.264\varphi(\mathrm{N_{2p}})\)。
- 理论需氧量为 \(0.264\varphi(\mathrm{N_{2p}}) - \varphi(\mathrm{O_{2p}})\),因此空气过剩系数 \(\alpha = 1 + \cfrac{\varphi(\mathrm{O_{2p}})}{0.264\varphi(\mathrm{N_{2p}}) - \varphi(\mathrm{O_{2p}})}\)。
- 假如燃烧过程产生 \(\ce{CO}\),过剩氧量必须加以校正,即从测得的过剩氧中减去氧化 \(\ce{CO}\) 为 \(\ce{CO2}\) 所需要的氧。因此:\(\alpha = 1 + \cfrac{\varphi(\mathrm{O_{2p}}) - 0.5\varphi(\mathrm{CO_{p}})}{0.264\varphi(\mathrm{N_{2p}}) - [\varphi(\mathrm{O_{2p}}) - 0.5\varphi(\mathrm{CO_{p}})]}\)。
- 通过测定烟气中污染物的浓度,根据实际排烟量,很容易计算污染物的排放量。
第三章 颗粒污染物控制技术基础
- 大气污染控制中涉及到的颗粒物,一般是指所有大于分子的颗粒物,但实际的最小界限为 \(\pu{0.01 \mu m}\) 左右。
- 颗粒物的存在状态,可单个地分散于气体介质中,也可能因凝聚等作用使多个颗粒集合在一起,成为集合体的状态,它在气体介质中就像单一个体一样。此外,颗粒物还能从气体介质中分离出来,呈堆积状态存在,或者本来就呈堆积状态。一般将这种呈堆积状态存在的颗粒物称为粉体。考虑到一般工程技术中的习惯,也通称为粉尘。
3.1 颗粒的粒径及粒径分布
3.1.1 颗粒的粒径
- 若颗粒是球形的,则可用其直径作为颗粒的代表性尺寸。但实际颗粒的形状多是不规则的,所以需要按一定的方法确定一个表示颗粒大小的代表性尺寸,作为颗粒的直径,简称为粒径。
- 常用的粒径定义方法:
- 显微镜法:
- 定向直径(\(d_{\mathrm {F}}\)):各颗粒在投影图中同一方向上的最大投影长度。
- 定向面积等分直径(\(d_{\mathrm {M}}\)):各颗粒在投影图中按同一方向将颗粒投影面积二等分的线段长度。
- 投影面积直径(\(d_{\mathrm {A}}\)):与颗粒投影面积相等的圆的直径。\(d_{\mathrm {A}} = \sqrt{\cfrac {4A}{\pi}}\)。
- 长径(\(d_{\mathrm {L}}\)):不考虑方向的最大长度。
- 短径(\(d_{\mathrm {b}}\)):不考虑方向的最小长度。
- 筛分法:
- 光散射法:
- 等体积直径(\(d_{\mathrm {V}}\)):与颗粒体积相等的圆球的直径。\(d_{\mathrm {V}} = \sqrt[3]{\cfrac {6V}{\pi}}\)。
- 沉降法:
- 斯托克斯直径(\(d_{\mathrm {s}}\)):同一流体中与颗粒的密度相同和沉降速度相等的圆球的直径。
- 空气动力学当量直径(\(d_{\mathrm {a}}\)):同一流体中与颗粒的密度相同和沉降速度相等的单位密度(\(\rho_{\mathrm p} = \pu{1g/cm3}\))的圆球的直径。
3.1.2 粒径分布
- 个数分布:
- 按粒径间隔给出个数分布测定数据,\(n_i\) 为每一间隔测得的颗粒的个数,\(N = \sum n_i\) 为颗粒的总个数。据此可以作出个数分布的其他定义。
- 个数频率:\(f_i = \cfrac {n_i}{\sum n_i}\),并有\(\sum\limits^{N}f_i = 1\)。
- 个数筛下累积频率:小于第 \(i\) 间隔上限粒径的所有颗粒个数与颗粒总个数之比,即 \(F_i = \cfrac {\sum\limits^{i} n_i}{\sum\limits^{N} n_i}\) 或 \(F_i = {\sum\limits^{i} f_i}\),并有 \(F_N = {\sum\limits^{N} f_i} = 1\)。
- 类似地可以定义个数筛上累积频率。
- 由累积频率曲线可以求出任意粒径间隔的频率 \(f\) 值。\(f_{a-b} = F_a - F_b = \int^{F_a}_{F_b} \mathrm dF = \int^{d_{\mathrm pa}}_{d_{\mathrm pb}} p\cdot\mathrm dd_{\mathrm p}\)。
- 个数频率密度:\(p(d_{\mathrm p}) = \cfrac {\mathrm dF}{\mathrm dd_{\mathrm p}}\)。
- 计算每一间隔的平均频度 \(\overline{p_i} = \cfrac {\Delta F_i}{\Delta d_{\mathrm pi}} = \cfrac {f_i}{\Delta d_{\mathrm pi}}\),按 \(\overline{p_i}\) 值对间隔中值 \(d_{\mathrm pi}\) 作出个数频率密度分布曲线。
- \(F = \int_0^{d_{\mathrm p}} p\cdot\mathrm dd_{\mathrm p}\),\(F_{\mathrm N} = \int_0^{+\infty} p\cdot\mathrm dd_{\mathrm p} = 1\)。
- \(F\) 曲线是有一拐点的“S”形曲线,拐点发生在个数频率密度 \(p\) 为最大值时对应的粒径处,这一粒径称为众径 \(d_{\mathrm {d}}\)。此处 \(\cfrac {\mathrm dp}{\mathrm dd_{\mathrm p}} = \cfrac {\mathrm d^2F}{\mathrm dd_{\mathrm p}^2} = 0\)。
- \(F = 0.5\) 时对应的粒径 \(d_{50}\) 称为个数中位直径(\(\mathrm {NMD}\))。
- 质量分布:
- 以颗粒个数给出的粒径分布数据,可以转换为以颗粒质量表示的粒径分布数据,或者进行相反的换算。这是根据所有颗粒都具有相同的密度,以及颗粒的质量与其粒径的立方成正比的假定进行的。可以按质量给出频率、筛下累积频率和频率密度的定义式。
- 质量频率:\(g_i = \cfrac {m_i}{\sum m_i} = \cfrac {n_id_{\mathrm pi}^3}{\sum\limits^{N} n_id_{\mathrm pi}^3}\)。
- 质量筛下累积频率:小于第 \(i\) 间隔上限粒径的所有颗粒个数与颗粒总个数之比,即 \(G_i = {\sum\limits^{i} g_i} = \cfrac {\sum\limits^{i}n_id_{\mathrm pi}^3}{\sum\limits^{N} n_id_{\mathrm pi}^3}\),并有 \(G_N = {\sum\limits^{N} g_i} = 1\)。
- 质量频率密度:\(q = \cfrac {\mathrm dG}{\mathrm dd_{\mathrm p}}\)。
- \(G = \int_0^{d_{\mathrm p}} q\cdot\mathrm dd_{\mathrm p}\),\(G_{\mathrm N} = \int_0^{+\infty} q\cdot\mathrm dd_{\mathrm p} = 1\)。
- \(G\) 曲线也是有一拐点的“S”形曲线,拐点发生在质量频率密度 \(q\) 为最大值时对应的粒径处,这一粒径称为质量众径。
- \(G = 0.5\) 时对应的粒径 \(d_{50}\) 称为质量中位直径(\(\mathrm {MMD}\))。
3.1.3 平均粒径
- 长度平均(或算数平均)粒径:\(\overline{d_L} = \cfrac {\sum n_id_{\mathrm pi}}{\sum n_i} = \sum f_id_{\mathrm pi} = \cfrac {\sum g_i/d_{\mathrm pi}^2}{\sum g_i/d_{\mathrm pi}^3}\)。
- 表面积平均粒径:\(\overline{d_S} = \sqrt{\cfrac {\sum n_id_{\mathrm pi}^2}{\sum n_i}} = \sqrt{\sum f_id_{\mathrm pi}^2} = \sqrt{\cfrac {\sum g_i/d_{\mathrm pi}}{\sum g_i/d_{\mathrm pi}^3}}\)。
- 体积平均粒径:\(\overline{d_V} = \sqrt[3]{\cfrac {\sum n_id_{\mathrm pi}^3}{\sum n_i}} = \sqrt[3]{\sum f_id_{\mathrm pi}^3} = \sqrt[3]{\cfrac {1}{\sum g_i/d_{\mathrm pi}^3}}\)。
- 表面积-体积平均粒径:\(\overline{d_{SV}} = \cfrac {\sum n_id_{\mathrm pi}^3}{\sum n_id_{\mathrm pi}^2} = \cfrac {\sum f_id_{\mathrm pi}^3}{\sum f_id_{\mathrm pi}^2} = \cfrac {1}{\sum g_i/d_{\mathrm pi}}\)。
- 几何平均粒径:\(d_{\mathrm g} = (d_1d_2\cdots d_N)^{1/N}\),或\(d_{\mathrm g} = (d_1^{n_1}d_2^{n_2}\cdots d_n^{n_N})^{1/N}\)。
- 按 \(\ln d_{\mathrm g}\) 表示的几何平均粒径:\(\ln d_{\mathrm g} = \cfrac {\sum n_i\ln d_{\mathrm pi}}{N}\),或 \(d_{\mathrm g} = \mathrm e^{\frac {\sum n_i\ln d_{\mathrm pi}}{N}}\)。
- 对于频率密度分布曲线是对称性的分布(如正态分布),其众径 \(d_{\mathrm d}\)、中位直径 \(d_{50}\) 和算数平均粒径 \(\overline{d_L}\) 相等;对于非对称性,\(d_{\mathrm d} < d_{50} < \overline{d_L}\)。
- 对于单分散气溶胶,所有颗粒的粒径相同,\(\overline{d_L} = d_{\mathrm g}\);否则,\(\overline{d_L} > d_{\mathrm g}\)。
3.1.4 粒径分布函数
- 正态分布(高斯分布):
- 频率密度:\(p(d_{\mathrm p}) = \cfrac {1}{\sigma\sqrt{2\pi}}\mathrm e^{-\frac {(d_{\mathrm p} - \overline{d_{\mathrm p}})^2}{2\sigma^2}}\)。
- 筛下累计频率:\(F(d_{\mathrm p}) = \cfrac {1}{\sigma\sqrt{2\pi}}\int_0^{d_{\mathrm p}}\mathrm e^{-\frac {(d_{\mathrm p} - \overline{d_{\mathrm p}})^2}{2\sigma^2}}\mathrm dd_{\mathrm p}\)。
- 其中,\(d_{\mathrm p}\) 为平均粒径 \(\overline{d_L}\),\(\sigma\) 为标准差,\(\sigma = \sqrt{\cfrac {\sum{n_i(d_{\mathrm pi} - \overline{d_{\mathrm p}})^2}}{N - 1}}\)。
- \(F\) 曲线在正态概率坐标纸上为一条直线,其斜率决定于标准差 \(\sigma\) 值。\(\sigma = d_{84.1} - d_{50} = d_{50} - d_{15.9} = \cfrac 12 (d_{84.1} - d_{15.9})\)。
- 对数正态分布:是最常用的粒径分布函数。以粒径的对数 \(\ln d_{\mathrm p}\) 代替粒径 \(d_{\mathrm p}\) 作出频率密度 \(p\) 曲线,得到一向正态分布一样的对称性钟形曲线,则认为该粉尘粒径分布符合对数正态分布。
- \(F(d_{\mathrm p}) = \cfrac {1}{\sqrt{2\pi}\ln\sigma_{\mathrm g}}\int_{-\infty}^{\ln d_{\mathrm p}}\mathrm e^{-\left(\frac {\ln d_{\mathrm p}/{d_{\mathrm g}}}{\sqrt 2\ln\sigma_{\mathrm g}}\right)^2}\mathrm d(\ln d_{\mathrm p})\)。
- \(p(d_{\mathrm p}) = \cfrac {1}{\sqrt{2\pi}d_{\mathrm p}\ln\sigma_{\mathrm g}}\mathrm e^{-\left(\frac {\ln d_{\mathrm p}/{d_{\mathrm g}}}{\sqrt 2\ln\sigma_{\mathrm g}}\right)^2}\)。
- 其中,\(d_{\mathrm g}\) 为几何平均粒径,\(\sigma_{\mathrm g}\) 为几何标准差,\(\ln \sigma_{\mathrm g} = \sqrt{\cfrac {\sum{n_i(\ln d_{\mathrm pi}/d_{\mathrm g})^2}}{N - 1}}\)。
- \(\sigma_{\mathrm g} = \cfrac{d_{84.1}}{d_{50}} = \cfrac{d_{50}}{d_{15.9}} = \sqrt{\cfrac{d_{84.1}}{d_{15.9}}}\)。
- 如果某种粉尘的粒径分布符合对数正态分布,则无论是质量分布、个数分布,还是表面积分布,它们的几何标准差 \(\sigma_{\mathrm g}\) 相等。\(\text{MMD}\) 表示质量中位直径,\(\text{NMD}\) 表示个数中位直径,\(\text{SMD}\) 表示表面积中位直径,则三者的换算关系为:\(\ln \text{MMD} = \ln \text{NMD} + 3\ln^2 \sigma_{\mathrm g}\),\(\ln \text{SMD} = \ln \text{NMD} + 2\ln^2 \sigma_{\mathrm g}\)。
- 算术平均粒径:\(\ln \overline{d_L} = \ln \text{NMD} + \cfrac12\ln^2 \sigma_{\mathrm g}\)。
- 表面积平均粒径:\(\ln \overline{d_S} = \ln \text{NMD} + \ln^2 \sigma_{\mathrm g}\)。
- 体积平均粒径:\(\ln \overline{d_V} = \ln \text{NMD} + \cfrac32\ln^2 \sigma_{\mathrm g}\)。
- 表面积-体积平均粒径:\(\ln \overline{d_{SV}} = \ln \text{NMD} + \cfrac52\ln^2 \sigma_{\mathrm g}\)。
3.2 粉尘的物理性质
- 密度:
- 单位体积粉尘的质量称为粉尘的密度,单位为 \(\pu{kg/m3}\) 或 \(\pu{g/cm3}\)。
- 真密度 \(\rho_{\mathrm p}\):以真实体积(不包括粉尘颗粒之间和颗粒内部的空隙体积)求得的密度。
- 堆积密度 \(\rho_{\mathrm b}\):以堆积体积(包括粉尘颗粒之间和颗粒内部的空隙体积)求得的密度。
- 对同一种粉尘来说,\(\rho_{\mathrm b} = (1 - \varepsilon)\rho_{\mathrm p}\),其中 \(\varepsilon\) 为空隙率。
- 安息角与滑动角:
- 安息角:粉尘从漏斗连续落到水平面上,自然堆积成一个圆锥体,圆锥体母线与水平面的交角。安息角小的粉尘,其流动性好。
- 滑动角:自然堆放在光滑平板上的粉尘,随平板做倾斜运动时,粉尘开始发生滑动时的平板倾斜角。
- 比表面积:
- 以粉尘自身体积(净体积)为基准表示的比表面积 \(S_V = \cfrac {\bar S}{\bar V} = \cfrac {6}{\overline{d_SV}}\)。
- 以粉尘质量为基准表示的比表面积 \(S_m = \cfrac {\bar S}{\rho_{\mathrm p}\bar V} = \cfrac {6}{\rho_{\mathrm p}\overline{d_SV}}\)。
- 以堆积体积为基准表示的比表面积 \(S_{\mathrm b} = (1 - \varepsilon)S_V = (1 - \varepsilon)\cfrac {\bar S}{\bar V} = (1 - \varepsilon)\cfrac {6}{\overline{d_SV}}\)。
- 含水率:粉尘中所含水分质量与粉尘总质量之比。
- 润湿性:粉尘颗粒与液体接触后能否相互附着或附着难易程度的性质。
- 当尘粒与液体接触时,如果接触面能扩大而相互附着,则称为润湿性粉尘;如果接触面趋于缩小而不能附着,则称为非润湿性粉尘。
- 粉尘的润湿性是选用湿式除尘器的主要依据。
- 荷电性和导电性:
- 荷电性:天然粉尘和工业粉尘几乎都带有一定的电荷(正电荷或负电荷)。电除尘器就是利用粉尘荷电而除尘的,在袋式除尘器和湿式除尘器中也可利用粉尘或液滴荷电来进一步提高对细尘粒的不急性能。
- 导电性:通常用电阻率来表示:\(\rho_{\mathrm d} = \cfrac {V}{J\delta}\),其中 \(V\) 为通过粉尘层的电压,\(J\) 为通过粉尘层的电流密度,\(\delta\) 为粉尘层的厚度。
- 高温时主要靠粉尘本体内部的电子或离子进行,低温时主要靠尘粒表面吸附的水分或其他化学物质中的离子进行。中间温度均存在。
- 高温范围内电阻率随温度升高而降低,低温范围内电阻率随温度升高而增大。中间温度均较弱,电阻率达到最大值。
- 黏附性:粉尘颗粒附着在固体表面上,或者颗粒彼此相互附着的现象称为黏附。
- 黏附力分为分子力(范德华力)、毛细力、静电力(库仑力)。
- 通常用粉尘层的断裂强度表示。
- 自燃性和爆炸性:
- 自燃性:粉尘在常温下存放过程中自然发热,此热量经长时间的积累,达到该粉尘的燃点而引起燃烧。来源:氧化热、分解热、聚合热、发酵热。
- 爆炸性:可燃物的剧烈氧化作用,在瞬间产生大量的热量和燃烧产物,在空间造成很高的温度和压力。条件:可燃混合物达到浓度范围、能量。
3.3 净化装置的性能
- 评价净化装置性能的指标,包括技术指标和经济指标两方面。
3.3.1 净化装置技术性能的表示方法
- 处理气体流量:由于本体漏气等原因,往往装置进口和出口的气体流量不同,因此用两者的平均值作为处理气体流量的代表。\(q_{V, \mathrm N} = \cfrac 12(q_{V, 1\mathrm N} + q_{V, 2\mathrm N})\)。
- 净化装置漏风率 \(\delta = \cfrac {q_{V, 1\mathrm N} - q_{V, 2\mathrm N}}{q_{V, 1\mathrm N}} \times 100~\%\)。
- 净化效率:是表示装置净化污染物效果的重要技术指标。
- 压力损失:装置的进口和出口气流全压之差。\(\Delta p = \zeta\cfrac {\rho v_1^2}{2}\),其中 \(\zeta\) 是净化装置的压力损失系数,\(v_1\) 是装置进口气流速度,\(\rho\) 是气体的密度。
3.3.2 净化效率的表示方法
- 总效率:同一时间内净化装置去除的污染物数量与进入装置的污染物数量之比。
- 装置进(出)口的气体流量为 \(q_{V, 1\mathrm N}\)(\(q_{V, 2\mathrm N}\))、污染物流量为 \(q_{m, 1}\)(\(q_{m, 2}\)),污染物浓度为 \(\rho_{1\mathrm N}\)(\(\rho_{2\mathrm N}\)),装置捕集的污染物流量为 \(q_{m, 3}\)。
- \(\eta = \cfrac {q_{m, 3}}{q_{m, 1}} = 1 - \cfrac {q_{m, 2}}{q_{m, 1}}\),或 \(\eta = 1 - \cfrac {\rho_{2\mathrm N}q_{V, 2\mathrm N}}{\rho_{1\mathrm N}q_{V, 1\mathrm N}}\)。
- 通过率:当净化效率很高时,或为了说明污染物的排放率,有时采用通过率来表示装置性能。\(P = \cfrac {q_{m, 2}}{q_{m, 1}} = 1 - \eta\)。
- 分级除尘效率:表示除尘效率与粉尘粒径的关系。
- 除尘器进口、出口和补给的 \(d_{\mathrm pi}\) 颗粒质量流量分别为 \(q_{m, 1i}\)、\(q_{m, 2i}\)、\(q_{m, 3i}\),则该除尘器对 \(d_{\mathrm pi}\) 颗粒的分级效率为:\(\eta_i = \cfrac {q_{m, 3i}}{q_{m, 1i}} = 1 - \cfrac {q_{m, 2i}}{q_{m, 1i}}\)。
- \(\eta_i = 50~%\) 对应的粒径称为除尘器的分割粒径 \(d_{\mathrm c}\)。
- 由总效率求分级效率:
- \(\eta_i = \cfrac {q_{m, 3}g_{3i}}{q_{m, 1}g_{1i}} = \eta \cfrac{g_{3i}}{g_{1i}}\);
- \(\eta_i = 1 - \cfrac {q_{m, 2}g_{2i}}{q_{m, 1}g_{1i}} = 1 - P\cfrac{g_{2i}}{g_{1i}}\);
- \(\eta_i = \cfrac {\eta}{\eta + Pg_{2i}/g_{3i}}\)。
- 由分级效率求总除尘效率:\(\eta = \sum \eta_ig_{1i}\)。
- 多级串联运行时的总净化效率:
- 总分级通过率:\(P_{i\mathrm T} = P_{i1}P_{i2}\cdots P_{in}\)。
- 总分级效率:\(\eta_{i\mathrm T} = 1 - (1 - \eta_{i1})(1 - \eta_{i2})\cdots(1 - \eta_{in})\)。
3.4 颗粒捕集的理论基础
3.4.1 流体阻力
- 流体阻力包括形状阻力、摩擦阻力,其大小取决于颗粒的形状、粒径、表面特性、运动速度及流体的种类和性质。
- \(F_{\mathrm D} = \cfrac 12C_{\mathrm D}A_{\mathrm p}\rho u^2\),其中 \(C_{\mathrm D}\) 是阻力系数,\(A_{\mathrm p}\) 是颗粒在其运动方向上的投影面积,\(\rho\) 是流体的密度,\(u\) 是颗粒与流体之间的相对运动速度。
- 阻力系数是雷诺数的函数,\(Re_{\mathrm p} = \cfrac {d_{\mathrm p}\rho u}{\mu}\),其中 \(d_{\mathrm p}\) 是颗粒的定性尺寸,\(\mu\) 是流体的黏度。
- 当 \(Re_{\mathrm p} \le 1\) 时,颗粒运动处于层流状态,近似有 \(C_{\mathrm D} = \cfrac {24}{Re_{\mathrm p}}\)。对于球形颗粒有 \(F_{\mathrm D} = 3\pi\mu d_{\mathrm p}u\),即斯托克斯阻力定律。称为斯托克斯区域。
- 当 \(1 < Re_{\mathrm p} < 500\) 时,颗粒运动处于湍流过渡区,近似有 \(C_{\mathrm D} = \cfrac {18.5}{Re_{\mathrm p}^{0.6}}\)。
- 当 \(500 < Re_{\mathrm p} < 2\times10^5\) 时,颗粒运动处于湍流状态,近似有 \(C_{\mathrm D} = 0.44\)。
- 当颗粒尺寸小到与气体分子平均自由程大小差不多时,颗粒开始脱离与气体分子接触,颗粒运动发生所谓“滑动”。在斯托克斯定律中引入坎宁汉修正系数 \(C\),则流体阻力 \(F_{\mathrm D} = \cfrac {3\pi\mu d_{\mathrm p}u}{C}\)。
- 坎宁汉修正系数的值取决于克努森数 \(Kn = \cfrac {2\lambda}{d_{\mathrm p}}\):\(C = 1 + Kn\left(1.257 + 0.400\mathrm e^{-\frac{1.10}{Kn}}\right)\)。
- 气体分子平均自由程 \(\lambda = \cfrac {\mu}{0.499 \rho\bar v}\),其中 \(\bar v\) 为气体分子的算术平均速度,\(\bar v = \sqrt{\cfrac{8RT}{\pi M}}\)。
- 近似计算:\(\pu{293 K}\) 和 \(\pu{101325 Pa}\) 下,\(C = 1 + \cfrac {0.165}{d_{\mathrm p}}\),\(d_{\mathrm p}\) 单位为 \(\pu{\mu m}\)。
3.4.2 阻力导致的减速运动
- 根据牛顿第二定律 \(\cfrac {\pi d_{\mathrm p}^3}{6} \rho_{\mathrm p} \cfrac {\mathrm du}{\mathrm dt} = -F_{\mathrm D} = -C_{\mathrm D}\cfrac {\pi d_{\mathrm p}^2}{4} \cfrac {\rho u^2}{2}\),即 \(\cfrac{\mathrm du}{\mathrm dt} = -\cfrac {3}{4} C_{\mathrm D}\cfrac {\rho}{\rho_{\mathrm p}}\cfrac {u^2}{d_{\mathrm p}}\)。
- \(Re_{\mathrm p}\) 不超过几百时,忽略速度对 \(C_{\mathrm D}\) 的影响。
- 斯托克斯区域内,\(\cfrac{\mathrm du}{\mathrm dt} = -\cfrac {18 \mu}{d_{\mathrm p}^2\rho_{\mathrm p}}u = -\cfrac {u}{\tau}\),其中 \(\tau = \cfrac {d_{\mathrm p}^2\rho_{\mathrm p}}{18 \mu}\),称为弛豫时间。
- 在 \(t = 0\) 时运动速度为 \(u_0\) 的颗粒,减速到 \(u\) 所需的时间 \(t = \tau\ln\cfrac{u_0}{u}\)。
- 在时间 \(t\) 时颗粒的速度 \(u = u_0\mathrm e^{-\frac {t}{\tau}}\)。
- 颗粒由初速度 \(u_0\) 减速到 \(u\) 所迁移的距离 \(x = \tau(u_0 - u)\)。
- 颗粒的停止距离 \(x_{\mathrm s} = \tau u_0\)。
- 滑流区域引入坎宁汉修正系数 \(C\)。
3.4.3 重力沉降
- 在静止流体中的单个球形颗粒,在重力作用下沉降时,\(F_{\mathrm D} = F_{\mathrm G} - F_{\mathrm B} = \cfrac {\pi d_{\mathrm p}^3}{6}(\rho_{\mathrm p} - \rho)g\)。
- 斯托克斯区,\(u_{\mathrm s} = \cfrac {d_{\mathrm p}^2(\rho_{\mathrm p} - \rho)g}{18 \mu}\)。
- 湍流过渡区,\(u_{\mathrm s} = \cfrac {0.153d_{\mathrm p}^{1.14}(\rho_{\mathrm p} - \rho)^{0.714}g^{0.714}}{\mu^{0.428}\rho^{0.286}}\)。
- 牛顿区,\(u_s = 1.74\sqrt{\cfrac {d_{\mathrm p}(\rho_{\mathrm p} - \rho)g}{\rho}}\)。
- 对于较大的球形颗粒,\(u_{\mathrm s} = \sqrt{\cfrac {4d_{\mathrm p}(\rho_{\mathrm p} - \rho)g}{3C_{\mathrm D}\rho}}\)。
- 斯托克斯直径:\(d_{\mathrm s} = \sqrt{\cfrac{18\mu u_{\mathrm s}}{\rho_{\mathrm p}gC}}\),空气动力学当量直径:\(d_{\mathrm a} = \sqrt{\cfrac{18\mu u_{\mathrm s}}{1000gC}}\),二者关系 \(d_{\mathrm a} = d_{\mathrm s}\sqrt{\cfrac{\rho_{\mathrm p}C}{C_{\mathrm a}}}\)。
3.4.4 离心沉降
- 离心力 \(F_{\mathrm c} = \cfrac {\pi}{6}d_{\mathrm p}^3\rho_{\mathrm p}\cfrac{u_{\mathrm t}^2}{R}\)。
- 末端速度 \(u_{\mathrm c} = \cfrac {d_{\mathrm p}^2\rho_{\mathrm p}}{18 \mu} \cfrac{u_{\mathrm t}^2}{R} = \tau a_{\mathrm c}\)。
3.4.5 静电沉降
- 静电力 \(F_{\mathrm E} = qE\)。
- 末端速度(驱进速度) \(\omega = \cfrac {qE}{3\pi\mu d_{\mathrm p}}\)。
3.4.6 惯性沉降
- 惯性碰撞:捕集效率取决于三个因素。
- 气流速度在捕集体周围的分布:\(Re_{\mathrm D} = \cfrac {u_0\rho D_{\mathrm c}}{\mu}\)。在高 \(Re_{\mathrm D}\) 下,除了临近捕集体表面附近外,气流流型与理想气体一致;当 \(Re_{\mathrm D}\) 较低时,气流受黏性力支配。
- 颗粒的运动轨迹:取决于颗粒的质量、气流阻力、捕集体的尺寸、形状及气流速度。碰撞参数 \(St = \cfrac {x_{\mathrm s}}{D_{\mathrm c}} = \cfrac {u_0\tau C}{D_{\mathrm c}}\)。
- 颗粒对捕集体的附着:通常假定与捕集体碰撞的颗粒能 \(100~\%\) 附着。
- 拦截:
- 直接拦截比 \(R = \cfrac {d_{\mathrm p}}{D_{\mathrm c}}\)。
- \(St\) 很大时,拦截效率为:圆柱形 \(\eta_{\mathrm {DI}} = R\),球形 \(\eta_{\mathrm {DI}} = 2R\)。
- \(St\) 很小时,拦截效率为:
- 圆柱体势流 \(\eta_{\mathrm {DI}} = 2R\),球体势流 \(\eta_{\mathrm {DI}} = 3R\)。
- 圆柱体黏性流 \(\eta_{\mathrm {DI}} = \cfrac {R^2}{2.002 - \ln Re_{\mathrm D}}\),球体黏性流 \(\eta_{\mathrm {DI}} = \cfrac {3R^2}{2}\)。
3.4.7 扩散沉降
- 扩散系数和均方根位移:
- 对于粒径约等于或大于气体分子平均自由程(\(Kn \le 0.5\))的颗粒,可用爱因斯坦公式计算:\(D = \cfrac {CkT}{3\pi\mu d_{\mathrm p}}\)。
- 对于粒径大于气体分子但小于气体分子平均自由程(\(Kn > 0.5\))的颗粒,可用朗缪尔公式计算:\(D = \cfrac {4kT}{3\pi d_{\mathrm p}^2p}\sqrt{\cfrac {8RT}{\pi M}}\)。
- 由于布朗扩散,颗粒在时间 \(t\) 内沿 \(x\) 轴的均方根位移为 \(\bar x = \sqrt{2Dt}\)。
- 扩散沉降效率:
- 佩克莱数:\(Pe = \cfrac {u_0D_{\mathrm c}}{D}\),是由惯性力产生的颗粒的迁移量与布朗扩散产生的颗粒的迁移量之比。
- 对于黏性流,\(\eta_{\mathrm {BD}} = \cfrac {1.71Pe^{-2/3}}{(2 - \ln Re_{\mathrm D})^{1/3}}\)。
- 对于势流,\(\eta{\mathrm {BD}} = \cfrac {3.19}{Pe^{1/2}}\)。
- 对于孤立的单个球形捕集体,\(\eta{\mathrm {BD}} = \cfrac {8}{Pe} + 2.23 Re_{\mathrm D}^{1/8}Pe^{-5/8}\)。
- 对于大颗粒的捕集,布朗扩散的作用很小,主要靠惯性碰撞作用;反之,对于很小的颗粒,惯性碰撞的作用微乎其微,主要是靠扩散沉降。
第四章 除尘装置
- 从气体中去除或捕集固态或液态微粒的设备称为除尘装置,或除尘器。
4.1 机械除尘器
- 机械除尘器通常指利用质量力(重力、惯性力和离心力等)的作用使颗粒物与气流分离的装置。
4.1.1 重力沉降室
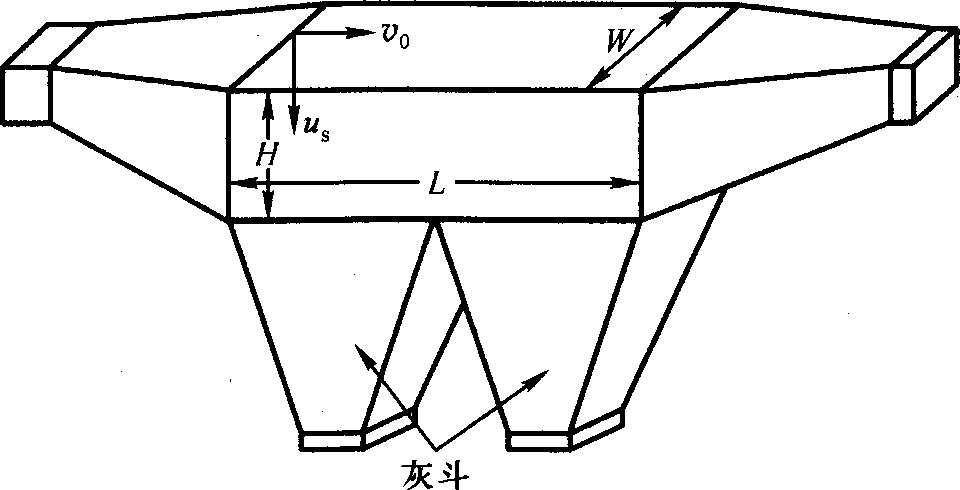 简单的重力沉降室
简单的重力沉降室
- 重力沉降室是通过重力作用使尘粒从气流中沉降分离的除尘装置。含尘气流进入重力沉降室后,由于扩大了流动截面积而使气体流速大大降低,使较重颗粒在重力作用下缓慢向灰斗沉降。
- 层流式重力沉降室:
- 假定:
- 在沉降室内气流为柱塞流,流速为 \(v_0\),流动状态保持在层流范围内,颗粒均匀地分布在烟气中。
- 在垂直方向,忽略浮力,仅在重力和气体阻力的作用下,每个例子以其沉降速度 \(u_{\mathrm s}\) 独立沉降。
- 在水平方向,粒子和气流具有相同的速度。
- 设沉降室长 \(L\)、宽 \(W\)、高 \(H\),处理烟气量 \(q_V\)。气流在沉降室内的停留时间为 \(t = \cfrac {L}{v_0} = \cfrac {LWH}{q_V}\)。
- 在时间 \(t\) 内,粒径为 \(d_{\mathrm p}\) 的离子的沉降距离为:\(h_{\mathrm c} = u_{\mathrm s}t = \cfrac {u_{\mathrm s}L}{v_0} = \cfrac {u_{\mathrm s}LWH}{q_V}\)。
- 当 \(h_{\mathrm c} < H\) 时,粒子的分级除尘效率 \(\eta_i = \cfrac {h_{\mathrm c}}{H} = \cfrac {u_{\mathrm s}L}{v_0H} = \cfrac {u_{\mathrm s}LW}{q_V}\)。
- 假设位于斯托克斯区,则能 \(100~\%\) 捕集的最小粒子直径 \(d_{\mathrm {min}} = \sqrt{\cfrac {18\mu v_0H}{\rho_{\mathrm p}gL}} = \sqrt{\cfrac{18\mu q_V}{\rho_{\mathrm p}gWL}}\)。在 \(\pu{293 K}\) 和 \(\pu{101325 Pa}\) 下,对于 \(\rho = \pu{1 g/cm3}\)、\(d_{\mathrm p} < \pu{100 \mu m}\) 的粒子都可行。
- 由于沉降室内的扰动和返混,常用计算值的一半作为分级效率,用 \(36\) 代替 \(18\)。
- 提高沉降室除尘效率的主要途径:降低沉降室内的气流速度、增加沉降室长度、降低沉降室高度。
- 多层沉降室:\(\eta_i = \cfrac {u_{\mathrm s}LW(n+1)}{q_V}\)。
- 湍流式重力沉降室:
- 假定沉降室中气流为湍流状态,在垂直于气流方向的每个横截面上粒子完全混合,即各种粒径的离子都均匀分布于气流中。
- 粒径为 \(d_{\mathrm p}\) 的离子的分级除尘效率为 \(\eta_i = 1 - \mathrm e^{\frac {u_{\mathrm s}LW}{q_V}}\)。
- 重力沉降室的主要优点:结构简单、投资少、压力损失小、维修管理容易。缺点:体积大、效率低。只能作为高效除尘的预除尘装置,出去较大和较重的粒子。
4.1.2 惯性除尘器
- 除尘机理:在沉降室内设置各种形式的挡板,使含尘气流冲击在挡板上。气流方向发生急剧转变,借助尘粒本身的惯性力作用,使其与气流分离。
- 结构类型:
- 冲击式:以气流中粒子冲击挡板捕集较粗粒子。
- 反转式:通过改变气流流动方向而捕集较细粒子。
- 应用:
- 气流速度越高、气流方向转变角度越大、转变次数越多,净化效率越高、压力损失越大。
- 用于净化密度和粒径较大的金属或矿物性粉尘。
- 一般只用于多级除尘中的第一级除尘。
4.1.3 旋风除尘器
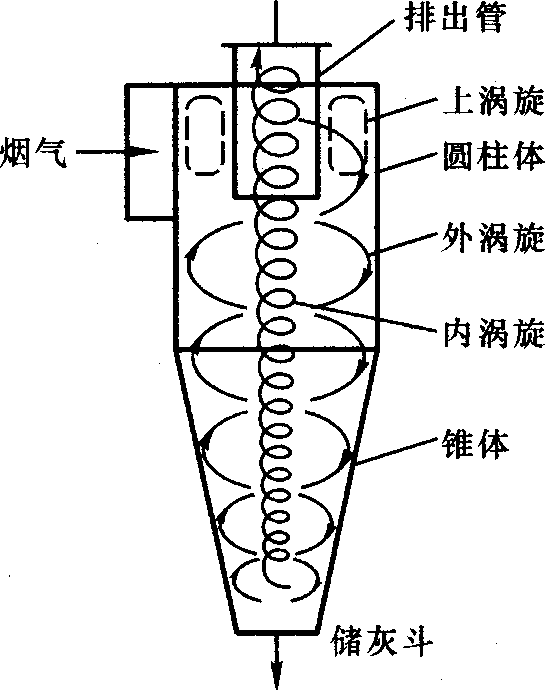 普通旋风除尘器的结构及内部气流
普通旋风除尘器的结构及内部气流
- 旋风除尘器是利用旋转气流产生的离心力使尘粒从气流中分离的装置,具有结构简单、应用广泛、种类繁多等特点。
- 气流与尘粒的运动:
- 含尘气流进入除尘器后,沿外壁由上向下作旋转运动,同时有少量气体沿径向运动到中心区域。当旋转气流的大部分到达锥体底部后,转而向上沿轴心旋转,最后经排出管派出。
- 旋转向下的外圈气流称为外涡旋,旋转向上的中心气流称为内涡旋。
- 切向速度:决定气流速度大小的主要速度分量,决定气流质点离心力大小的主要因素。
- 外涡旋:\(v_{\mathrm t}R^n = 常数\),其中 \(n \le 1\),称为涡流指数,\(n = 1 - (1 - 0.67D^{0.14})\left(\cfrac {T}{283}\right)^{0.3}\),其中 \(D\) 为旋风除尘器的直径,\(T\) 为气体的温度。
- 内涡旋:\(v_{\mathrm t} = \omega R\),其中 \(\omega\) 是气流的旋转角速度。
- 在内外涡旋交界圆柱面上,气流的切向速度最大。
- 径向速度:近似认为外涡旋气流均匀地经过内、外涡旋交界圆柱面进入内涡旋,其平均速度认为是外涡旋气流的平均径向速度 \(v_r = \cfrac {q_V}{2\pi r_0h_0}\)。
- 轴向速度:外涡旋向下;内涡旋向上,且随气流上升而增大。
- 压力损失:\(\Delta p = \cfrac 12 \xi\rho v_1^2\)。
- 除尘效率:
- 计算分割直径是确定除尘效率的基础。
- 粒子的沉降主要取决于离心力 \(F_{\mathrm C}\) 和阻力 \(F_{\mathrm D}\)。
- 如果 \(F_{\mathrm C} > F_{\mathrm D}\),则在离心力推动下移向外壁,被捕集。
- 如果 \(F_{\mathrm C} < F_{\mathrm D}\),则在向心气流的带动下进入内涡旋并排出。
- 如果 \(F_{\mathrm C} = F_{\mathrm D}\),则有 \(50~\%\) 几率被捕集,\(50~\%\) 几率被排出,此时的粒径即为分割粒径。
- 对于球形粒子,\(\cfrac {\pi}{6}d_{\mathrm c}^3\rho_{\mathrm p}\cfrac {v_{\mathrm t0}^2}{r_0} = 3\pi\mu d_{\mathrm c}v_r\),其中 \(v_{\mathrm t0}\) 为交界面处气流的切向速度,\(v_r\) 为平均径向速度。
- 求得 \(d_{\mathrm c} = \sqrt{\cfrac {18\mu v_rr_0}{\rho_{\mathrm p}v_{\mathrm t0}^2}}\),计算分级效率 \(\eta_i = 1 - \mathrm {exp}\left[-0.6931\times\left(\cfrac {d_{\mathrm p}}{d_{\mathrm c}}\right)^{\frac {1}{n + 1}}\right]\)。
- 另一种公式 \(\eta_i = \cfrac {(d_{\mathrm pi}/d_{\mathrm c})^2}{1 + (d_{\mathrm pi}/d_{\mathrm c})^2}\)。
- 影响因素:
- 二次效应:被捕集离子重新进入气流。
- 在较小粒径区间,理应逸出的粒子由于聚集或被较大尘粒撞向壁面,实际效率高于理论效率。
- 在较大粒径区间,理应降入灰斗的尘粒随净化后的气流一起拍走,实际效率低于理论效率。
- 比例尺寸:
- 相同的切向速度下,筒体直径 \(D\) 越小,粒子受到的惯性力越大,但粒子容易逃逸,使效率下降。
- 锥体适当加长,对提高除尘效率有利。
- 排出管直径越小,分割直径越小,除尘效率越高,但压力降增加,一般取排出管直径 \(d_{\mathrm e} = (0.4 \text{~} 0.65)D\)。
- 除尘器下部的严密性也是重要因素。
- 烟尘的物理性质:气体的密度和黏度、尘粒的大小和相对密度、烟气含尘浓度。
- 操作变量:提高烟气入口流速,分割直径变小。
- 旋风除尘器的结构形式:
- 按进气方式:切向进入式、轴向进入式,切向进入式又分为直入式和蜗壳式。
- 按气流组织:回流式、直流式、平旋式、旋流式。
- 多管旋风除尘器:由多个相同构造形状和尺寸的小型旋风除尘器组合在一个壳体内并联使用的除尘器组。常见回流式、直流式。
- 设计选型:
- 根据含尘浓度、粒度分布、密度等烟气特征及除尘要求、允许的压力损失和制造条件等因素全面分析,合理地选择旋风除尘器的类型。
- 根据使用时允许的压力降确定进口气速。
- 确定旋风除尘器的进口截面、入口宽度、高度。
- 确定各部分几何尺寸。
4.2 电除尘器
- 电除尘器是含尘气体在通过高压电场进行电离的过程中,使尘粒荷电,并在电场力的作用下使尘粒沉积在集尘极上,将尘粒从含尘气体中分离出来的一种除尘设备。
- 分离力直接作用在粒子上,而不是作用在整个气流上。分离粒子耗能小、气流阻力小。
- 主要优点:压力损失小、处理烟气量大、能耗低、对细粉尘有很高的捕集效率、可在高温或强腐蚀性气体下操作。
- 工作原理:
- 三个基本过程:悬浮粒子荷电、带电粒子在电场内迁移和捕集、将捕集物从集尘表面上清除。
- 高压直流电晕是使粒子荷电的最有效办法,广泛应用于静电除尘过程。
- 荷电粒子的捕集是使其通过延续的电晕电场或光滑的不放电的电极之间的纯静电场而实现。
- 通过振打除去接地电极上的灰层并使其落入灰斗。
- 电晕放电:发生在细金属电晕线和集尘板之间,或者发生在金属丝和金属管之间。
- 放电电极(电晕极)是一根曲率半径很小的纤细裸露电线,上端与直流电源的一极相连,下端由吊锤固定位置。集尘电极是具有一定面积的管和板,它与电源的另一极相连。
- 假设电晕电极为负极,从金属丝表面或附近放出的电子迅速向接地极或正极运动,与气体分子发生撞击并使之离子化,结果又产生了大量电子,通常称这种过程为雪崩过程。
- 起始电晕电压:开始产生电晕电流时所施加的电压。
- 经验公式 \(E_c = 3\times 10^6 m\left(\delta + 0.03\sqrt{\cfrac {\delta}{a}}\right)\),其中 \(\delta\) 为空气的相对密度,\(m\) 为导线光滑修正系数。
- 负电晕极:工业气体净化,稳定性强、可以得到较高操作电压和电流。
- 正电晕极:空气调节系统,产生的臭氧和氮氧化物的量低。
- 影响电晕特性的因素:电极的形状、电极间距离,气体组成、压力、温度,气流中要捕集的粉尘的浓度、粒度、电阻率以及它们在电晕极和集尘极上的沉积。
- 粒子荷电机制:
- 电场荷电(碰撞荷电):离子在静电力作用下作定向运动,与粒子碰撞而使粒子荷电。
- 扩散荷电:由离子的扩散现象而导致的粒子荷电过程。依赖于离子的热能,不依赖于电场。
- \(d_{\mathrm p} > \pu{0.5 \mu m}\) 的粒子,以电场荷电为主;\(d_{\mathrm p} < \pu{0.15 \mu m}\) 的粒子,以扩散荷电为主;\(\pu{0.15 \mu m} < d_{\mathrm p} < \pu{0.5 \mu m}\) 的粒子,需要同时考虑两种过程。
- 电场荷电饱和粒子电荷 \(Q = 3\pi \left(\cfrac {\varepsilon_{\mathrm r}}{\varepsilon_{\mathrm r} + 2}\right)\varepsilon_0d_{\mathrm p}^2E_0\),其中 \(\varepsilon_{\mathrm r}\) 是粒子相对介电常数,\(\varepsilon_0\) 是真空介电常数。
- 扩散荷电不存在最大极限值,时间 \(t\) 内粒子获得的电荷 \(Q_{\mathrm n} = \cfrac {2\pi\varepsilon_0 kTd_{\mathrm p}}{e^2}\ln\left(1 + \cfrac{e^2\bar ud_{\mathrm p}N_0t}{8\varepsilon_0kT}\right)\),其中 \(k\) 为玻尔兹曼常数,\(N_0\) 为离子密度,\(e\) 为电子电量,\(\bar u\) 为气体离子的平均热运动速度。
- 电场荷电和扩散荷电的综合作用:简单地将电场荷电的饱和电荷和扩散电荷的电荷相加,能近似地表示两种过程综合作用时的荷电量。
- 驱进速度:荷电粒子在电场力的作用下,向集尘极移动时,电场力与空气阻力很快就达到平衡。\(\omega = \cfrac {QE_{\mathrm p}}{3\pi\mu d_{\mathrm p}}\)。
- 捕集效率:德意希分级效率方程:\(\eta_i = 1 - \cfrac {\rho_{2i}}{\rho_{1i}} = 1 - \mathrm e^{-\frac AQ\omega_i}\)。
- 被捕集粉尘的清除
- 电晕极:振打清灰。
- 集尘极:湿式电除尘器用水冲洗集尘极板,干式电除尘器由机械撞击或电机振动产生的振动力清除。
- 结构:
- 电晕极:起晕电压低、电晕电流大、机械强度高、能维持准确的极间距离、易清灰。
- 集尘极:振打时粉尘的二次扬起少、单位集尘面积消耗金属量低、极板高度较大时有一定的刚性不易变形、振打时易于清灰造价低。
- 选择和设计:
- 比集尘板表面积的确定
- 长高比的确定
- 气流速度的确定
- 气体的含尘浓度
4.3 袋式除尘器
- 过滤式除尘器是使含尘气流通过过滤材料将粉尘分离捕集的装置。采用纤维织物作滤料的袋式除尘器,在工业尾气的除尘方面应用较广。
- 袋式除尘器的除尘效率一般可达 \(99~\%\) 以上。效率高,性能稳定可靠,操作简单。
- 工作原理
- 含尘气流从下部孔板进入圆筒形滤袋内,在通过滤料的孔隙时,粉尘被捕集在滤料上,透过滤料的清洁气体由排出口排出。沉积在滤料上的粉尘,可在机械振动的作用下从滤料表面脱落,落入灰斗中。
- 新鲜滤料的除尘效率较低。颗粒在滤袋表面形成粉尘层,常称为粉尘初层,提高了除尘效率。
- 除尘器阻力达到一定数值后,要及时清灰。清灰不应破坏粉尘初层。
- 一般来讲,除尘效率随过滤速度增加而下降。
- 压力损失
- 达西方程:\(\cfrac {\Delta p}{x} = \cfrac {v\mu_{\mathrm g}}{K}\),其中 \(K\) 是颗粒层或滤料的渗透率,\(x\) 是颗粒层或滤料厚度。
- 则有 \(\Delta p = \Delta p_{\mathrm f} + \Delta p_{\mathrm p} = \cfrac {x_{\mathrm c}\mu_{\mathrm g}v}{K_{\mathrm f}} + \cfrac {x_{\mathrm p}\mu_{\mathrm g}v}{K_{\mathrm p}}\),其中滤料的压力损失 \(\Delta p_{\mathrm f}\) 基本上是一个常数。
- 在时间 \(t\) 内,沉积在滤袋上的飞灰质量 \(m = vAt\rho\),其中 \(A\) 是滤袋的过滤面积,\(\rho\) 是烟气中的粉尘浓度。
- 则有 \(\Delta p_{\mathrm p} = \cfrac {v^2\rho t\mu_{\mathrm g}}{K_{\mathrm p}\rho_{\mathrm c}} = R_{\mathrm p}v^2\rho t\),其中 \(R_{\mathrm p}\) 是飞灰的比阻力系数。
- 估算 \(R_{\mathrm p} = \cfrac {\mu_{\mathrm g}S_0^2}{6\rho_{\mathrm p}C} = \cfrac{3 + 2\beta^{5/3}}{3 - 4.5\beta^{1/3} + 4.5\beta^{5/3} - 3\beta^2}\),其中 \(S_0\) 是比表面参数,\(S_0 = 6\left(\cfrac {10^{1.151} \lg^2 \sigma_{\mathrm g}}{\text{MMD}}\right)\),\(\beta = \cfrac {rho_{\mathrm c}}{\rho_{\mathrm p}}\)。
- 滤料:
- 要求:容尘量大、吸湿性小、效率高、阻力低、使用寿命长、耐温、耐磨、耐腐蚀、机械强度高。
- 种类:按材质分为天然纤维、无机纤维、合成纤维,按滤料结构分为滤布和毛毡。
- 清灰:机械振动清灰、逆气流清灰、脉冲喷吹清灰。
- 选择与设计:
- 选定除尘器形式、滤料及清灰方式。
- 计算过滤面积。
- 除尘器设计:确定滤袋尺寸,计算每条滤袋的面积、计算滤袋条数。
- 应用:
- 比电除尘器结构简单、投资省、可以回收高比电阻粉尘。
- 与文丘里洗涤器相比,动力消耗小,回收的干颗粒物便于综合利用。
4.4 湿式除尘器
- 湿式除尘器是使含尘气体与液体(一般为水)相互接触,利用水滴和颗粒的惯性碰撞及其作用捕集颗粒或使粒径增大的装置。湿式除尘器可以有效地将直径在 \(0.1 \text{~} \pu{20 \mu m}\) 的液态或固态粒子从气流中除去,同时也能脱除部分气态污染物。
- 优点:结构简单、造价低、占地面积小、操作及维修方便、净化效果高。
- 分类:重力喷雾洗涤器、旋风洗涤器、自激喷雾洗涤器、板式洗涤器、填料洗涤器、文丘里洗涤器、机械诱导喷雾洗涤器。
- 惯性碰撞参数:
- 除尘原理:主要是液滴和颗粒之间的惯性碰撞和拦截作用。惯性碰撞主要考虑尘粒质量,拦截作用主要考虑粒径大小。
- 定义惯性碰撞参数 \(N_{\mathrm I} = St = \cfrac {x_{\mathrm s}}{D_{\mathrm c}} = \cfrac {d_{\mathrm p}^2\rho_{\mathrm p}(u_{\mathrm p} - u_{\mathrm D})C}{18\mu d_{\mathrm D}}\)。对于粒径小于 \(\pu{5.0 \mu m}\) 的粒子,必须考虑坎宁汉修正系数 \(C\)。
- 除尘效率:对于势流和黏性流,\(\eta = 1 - \mathrm e^{-KL\sqrt{N_{\mathrm I}}}\),其中 \(K\) 是关联系数,\(L\) 是液气比。
- 拦截作用:拦截参数 \(K_{\mathrm p} = \cfrac {d_{\mathrm p}}{D_{\mathrm c}}\)。
- 接触功率:
- 总能量损失 \(E_{\mathrm t}\) 包括气体通过洗涤器时的能量损失 \(E_{\mathrm g}\) 和雾化喷淋液体过程中的能量损失 \(E_{\mathrm l}\),即 \(E_{\mathrm t} = E_{\mathrm g} + E_{\mathrm l} = \cfrac {1}{3600}\left(\Delta p_{\mathrm G} + p_{\mathrm L}\cfrac {q_{V, \mathrm L}}{q_{V, \mathrm G}}\right)\),其中 \(\Delta p_{\mathrm G}\) 是气体通过洗涤器的压力损失,\(p_{\mathrm L}\) 是液体入口压力。
- 为了关联接触功率和除尘效率,经常以传质单元数 \(N_{\mathrm t}\) 表示后者,其中 \(\eta = 1 - \mathrm{e}^{-N_{\mathrm t}}\)。
- 对于给定的洗涤器和颗粒物,有 \(N_{\mathrm t} = \alpha E_{\mathrm t}^\beta\)。
- 分割粒径:\(P_{\mathrm t} = \int_0^{+\infty}P_iq_i\mathrm dd_{\mathrm p}\)。
- 多数惯性分离装置的分级通过率可以表示为 \(P_i = \mathrm{exp}\left(-A_{\mathrm e}d_{\mathrm a}^{B_{\mathrm e}}\right)\)。
- 喷雾塔洗涤器:含尘气体向上运动,液滴由喷嘴喷出向下运动。
- 除尘效率 \(\eta = 1 - \mathrm {exp}\left[-\cfrac {3q_{V, \mathrm L}u_{\mathrm t}z\eta_{\mathrm d}}{2q_{V, \mathrm G}d_{\mathrm D}(u_{\mathrm t} - u_{\mathrm G})}\right]\)。其中 \(u_{\mathrm t}\) 是液滴的终端沉降速度,\(v_{\mathrm G}\) 是空塔断面气速,\(\eta_{\mathrm d}\) 是单个液滴的碰撞效率。
- 势流和黏性流时近似有 \(\eta_{\mathrm d} = \left(\cfrac {St}{St + 0.7}\right)^2\)。
- 对于粒子的惯性捕集,可用下式估算:\(P_{\mathrm t} = \mathrm{exp}\left(-\cfrac{3q_{V, \mathrm L}z\eta_{\mathrm d}}{2q_{V, \mathrm G}d_{\mathrm D}}\right)\)。
- 旋风洗涤器:在干式旋风分离器内部以环形方式安装一排喷嘴。含尘气体由筒体的下部切向引入,水通过轴上安装的多头喷嘴喷出,径向喷出的水雾与螺旋形旋转气流相碰,使颗粒被捕集下来。
- 压力损失:\(\Delta p = \Delta p_0 + \cfrac {q_{V, \mathrm L}}{q_{V, \mathrm G}}\rho_{\mathrm L}\overline{u_{\mathrm D}}^2\)。
- 文丘里洗涤器:文丘里洗涤器是一种高效湿式洗涤器。含尘气体由进气管进入收缩管后,流速逐渐增大,气流的压力能逐渐转变为动能。洗涤液(一般为水)通过喉管周边均匀分布的喷嘴进入,液滴被高速气流雾化和加速。
- 压力损失:\(\Delta p = -1.03\times 10^{-3}v_{\mathrm T}^2\cfrac {q_{V, \mathrm L}}{q_{V, \mathrm G}}\)。或者:\(\Delta p = 0.863\rho_{\mathrm G}A^{0.133}v_{\mathrm T}^2L^{0.78}\)。
- 除尘效率:\(P = \mathrm{exp}\left(-\cfrac {6.1\times10^{-9}\rho_{\mathrm L}\rho_{\mathrm p}Cd_{\mathrm p}^2f^2\Delta p}{\mu_{\mathrm G}^2}\right)\)。
4.5 除尘器的选择与发展
- 选择除尘器时必须考虑除尘效率、压力损失、一次投资、维修管理等。需要考虑:
- 必须满足排放标准规定的排放要求。
- 粉尘颗粒的物理性质对除尘器性能具有较大影响。
- 气体的含尘浓度。
- 烟气温度和其他性质。
- 粉尘的处理问题。
- 其他因素:位置、空间、环境条件、经济因素等。
- 发展:
- 除尘设备趋向高效率。
- 发展处理大烟气量的除尘设备。
- 着重研究提高现有高效除尘器的性能。
- 发展新型除尘设备。
- 重视除尘机理及理论方面的研究。


