前言
这是《环境研究方法》2019年秋季学期的“欺骗表单”(“Cheating Sheet”直译),内容由张祥伟、朱颖、屈玥坤、汤睿整理并补充。本页面提供的是在线阅读版本,如需打印,请从网盘相应路径查找。
课堂讲解内容
第1讲 环境系统和定量研究Ⅰ(陈琦,20190912)
1. 关于课程
- 科学研究的目的:基础研究:描述、预测、解释。应用研究:控制。
- 科学研究方法:
- 运用所学知识进行科学思维的技巧;从事科学研究过程中总结、提炼出来的;处在不断发展中;根据研究手段的不同,可以分为定性研究方法和定量研究方法;有较大的学科差异。
- 环境科学研究:
- “本法所称环境,是指影响人类生存和发展的各种天然的和经过人工改造的自然因素的总体,包括大气、水、海洋、土地、矿藏、森林、草原、湿地、野生生物、自然遗迹、人文遗迹、自然保护区、风景名胜区、城市和乡村等。”——《中华人民共和国环境保护法(2014年修订)》
- 大气复合污染:细颗粒物与臭氧、近半河流湖泊严重污染、全国土壤总超标率为16.1%(2014年)、能源与可持续发展、能源贫困、二氧化碳浓度升高、全球变暖。
- 经典理论:\(\ce{2NO + O2 -> 2NO2}\),而在大气组分的浓度水平下可能发生\(\ce{NO + O3 -> NO2 + O2}\)。结合实际极为重要。
- 特点:涉及面广,综合性强,密切联系实际。既包括基础科学,又是应用科学。在研究中需要宏观与微观结合,自然科学与社会科学结合,具备整体观。
2. 科学研究的基本概念
- “三观要正”:真实存在、有因果关系、有规律(符合一定的理论)。
- “讲究套路”:案例研究、特殊事件、类比延伸、归纳经验、对照/对比、简化思维、允许意外。
- 好的研究想法:找到一个感兴趣的领域;针对一个具体问题产生一个研究想法;基于自身经验知识,判断想法是否可行;查阅文献,基于前人研究结果,判断想法是否可行;咨询(导师);根据想法,提出研究假设开展研究设计。
- 一些定义:
- 什么是假设:如果理论A是正确的,则数据模式B将成立。
- 因果关系分析:A的出现导致或确定B的出现。
- 判定方式:共变性;暂且只考虑先因后果;控制了因就能控制果。
- 环境研究中往往是多变量的复杂情况,因果关系常是基于概率的而非决定性的,理解必要条件和充分条件。
- 机理型因果和目的型因果的不同:后者是后向目标,即把原因作为目标。
- 模型:一部分真理的简化描述。
- 变量和样本。
- 测量和数据:测量尺度。
- 定类测量:不排序。
- 定序测量:排序。
- 定距测量:无真正零值,如温度,0度不是没有温度。
- 定比测量:环境研究中常用,降水。
- 选择分析方法时,首先要确认变量的测量尺度。
- 离散变量和连续变量。
- 测量的精度:准确度、精密度。
3. 环境定量研究基础——自然环境系统
- 环境问题要考虑介质:
- 污染问题往往是单一介质问题:空气污染、水污染、土壤污染。
- 污染物存在多介质的迁移转化:环境中存在普遍物质交换。
- 环境涉及能量交换:环境自然系统中的定量研究立足于环境系统中的能量流和物质流。
- 物料平衡/质量守恒原理:对于控制体积边界,有输入、累积、反应(消耗和产生)、输出,累积速率 = 输入 - 输出 + (产生 - 消耗)。\(\cfrac {\mathrm dM}{\mathrm dt} = \cfrac {\mathrm {d(in)}}{\mathrm dt} - \cfrac {\mathrm {d(out)}}{\mathrm dt} + r\)。
- 时间是重要参数,对环境系统而言,浓度水平很重要,速率也很重要。
- 室内污染中的质量平衡——污染水平:例题1。
- 水污染中的质量平衡——污染水平:例题2 ~ 3。
第2讲 环境系统和定量研究Ⅱ(陈琦,20190919)
1. 环境系统中的物料平衡——反应器原理
- 充分混合体系:cout = ct,后者为控制体积内浓度。浓度不变时为稳态。
- 反应器原理:
- 间歇反应器:完全混合间歇反应器(CMBR)。
- 惰性物质:不反应,瞬时投放M0后,浓度直接变化至c0并保持不变(似稳态)。
- 活性物质:发生反应,一级反应时dc / dt = -kc,积分得ct = c0 exp(-kt)。
- 流式反应器:完全混合流反应器(CMFR),连续搅拌反应器(CSTR)。Qin = Qout = Q。平均停留时间t0 = V / Q。
- 惰性物质:dc / dt = c1Q / V - cQ / V,积分得ct = c0 exp(-t / t0) + c1[1 - exp(-t / t0)],其中c0为原始浓度,c1为输入浓度。无输入时c1 = 0。
- 活性物质:dc / dt = c1Q / V - cQ / V - kc,积分得ct = c0 exp[-(1 / t0 + k)t] + c1{1 - exp[-(1 / t0 + k)t]} / (1 + kt0)。稳态浓度c∞ = c1 / (1 + kt0)。
- 有控制体积内源排放的CMFR:V · dc / dt = QCin - QC - kdcV + kgV。
- 稳态浓度时dc / dt = 0,\(c = c_\infty + (c_0 - c_\infty) \exp\left[ -\left( k_{\mathrm d} + \cfrac {Q} {V} t \right) \right]\)。
- 有机物氧化、放射性物质衰减时,常用一级反应描述。例题4。
- 间歇反应器:完全混合间歇反应器(CMBR)。
- 完全不混合系统:也叫塞流或平推流,类似火车运货。
- 活塞流反应器(PFR):截面处流体和前后流体不发生混合,截面上可充分混合或不混合。Qin = Qout = Q。平均停留时间t0 = V / Q。
- 惰性物质:t0之前cout = 0,t0之后cout = cin。
- 活性物质:反应时间一定,t0之前cout = 0,t0之后cout = cin exp(-kt0)。例题5。
| 反应级数 | \(r\) | 间歇反应器 | 流式反应器 | 活塞流反应器 |
|---|---|---|---|---|
| 零级 | \(-k\) | \(c_0 / k\) | \((c_0 - c_t) / k\) | \((c_0 - c_t) / k\) |
| 一级 | \(-kc\) | \(1 / k\) | \([(c_0 - c_t) - 1] / k\) | \(\ln(c_0 / c_t) / k\) |
| 二级 | \(-2kc^2\) | \(1/(2kc_0)\) | \([(c_0 - c_t) - 1] / (2kc_t)\) | \([(c_0 - c_t) - 1] / (2kc_0)\) |
| 反应级数 | \(r\) | 间歇反应器 | 流式反应器 | 活塞流反应器 |
|---|---|---|---|---|
| 零级 | \(-k\) | \(c_0 - kt\) | \(c_0 - k\theta\) | \(c_0 - k\theta\) |
| 一级 | \(-kc\) | \(c_0\exp(-kt)\) | \(c_0 / (1 + k\theta)\) | \(c_0\exp(-k\theta)\) |
| 二级 | \(-2kc^2\) | \(c_0 / (1 + 2ktc_0)\) | \([(8k\theta c_0 + 1)^{1/2} - 1] / (4k\theta)\) | \(c_0 / (1 + 2k\theta c_0)\) |
- 非理想反应器:\(\cfrac {\partial c} {\partial t} = D_{\mathrm L} \cfrac {\partial ^ 2 c} {\partial z^2} - u \cfrac {\partial c} {\partial z}\)。
- 其他体系:
- 生物圈的质量平衡——种群数量(类似活塞流反应器),例题6。
- 资源利用中的质量平衡——有限资源。ts = F / A,能源耗竭所用时间、能源现存量、能源年需求量。现存量随年需求而增长:\(F = A\left[ \cfrac {(1 + i) ^ n - 1} {i} \right]\)。我国储量和产量比值为33年,考虑消耗增长(8%)为17年。
- 资源利用中的质量平衡——固废管理。再生资源回收时,质量存在衰减,一般按指数衰减简化,M = M0 exp(-kn)。循环利用利用率:\(\sum\limits_{k = 0}^n M_k = \cfrac {M_0(f^n - 1)} {f - 1}\),\(\sum\limits_{k = 0}^\infty M_k = \cfrac {M_0}{1 - f}\),其中f为回收率。
2. 能量平衡原理
- 符合热力学定律: 不会凭空产生、消失。
- 环境体系大多是开放体系:涉及穿过边界的物质流和能量流;既有能量流速率又有物质流速率。

第3讲 环境系统和定量研究Ⅲ(戴翰程,201909126)
- 星球边界 Planetary Boundary:九个对人类生存至关重要的“行星生命支持系统”/地球系统过程,以帮助定义“人类发展的安全空间”。
- 不安全的星球边界(2009):气候危机、生物多样性损失、N循环
- 环境经济系统中的“反应”
- 几个主体与行为:生产者与生产行为;消费者与消费行为;政府与政府干预;环境与污染行为;其他如贸易行为等
- “反应”的原则:几种平衡(物质/能源/价值平衡)
- “反应”的调控机制:价格机制
- 反应的模拟-→环境经济分析方法:分为
实证研究和实验研究
两种
- 实证研究: 依据基本经济学原理或实践经验,通过收集数据,开展计量或统计分析。(回归分析、投入产出分析、增长核算分析、统计分析、时间序列分析等)
- 实验研究: 先依据有关经济学理论建立行为方程和平衡方程(方程参数大多依据经验或校准获得),然后改变外生变量(如税收政策、能源价格等),对模型系统进行运算模拟得到结果。(可计算一般均衡模型、多主体模型、技术优化模型、系统动力学模型)
- 反应原则-几种平衡
- 物质平衡:总物质投入= 总物质输出+ 存量增加量;
- 物质流分析(Material Flow Analysis, MFA):是指在一定的时间和空间范围内系统地评价一个特定系统的物质流动和库存变化。在物流分析过程中,它结合了物质的源头、流通路径、流通的媒介和最终的去向等环节。→相关领域:城市代谢(Urban Metabolism)
- 全生命周期评价(Life Cycle Assessment):系统化地定量描述产品生命周期中的各种资源、能源消耗和环境排放并评价其环境影响的国际标准方法。→相关领域:产业生态学(Industrial Ecology)
- 能源平衡:能源平衡表(EBT,energy balance table),TPES总一次能源供应,TFC总终端能源
- 一次能源指自然界中以现成的形式存在,不经任何改变或转换的天然能源资源。如原煤、原油、页岩油、天然气、核燃料、水能、风能等。
- 石油依存度(%)=[TPES(oil)+TPES(petro)]/总TPES;进口依存度(%)= Total import/(Total import+Total production)
- 转换:Transformations,计算发电效率(一次能源→二次能源);能源转换损失=总TPES-总TFC
- 价值平衡:四个主体(居民-投资/劳动/消费;政府-征税/公共服务;企业-生产/发工资;环境-资源禀赋/环境承载);三种平衡(家庭收入与支出平衡;企业投入与产出平衡;市场供应与需求平衡);价格与弹性(供需曲线;市场均衡;价格与弹性);价值优化(利润/效用最大化;成本最小化)
- 物质平衡:总物质投入= 总物质输出+ 存量增加量;
- 投入产出表:
- ①以一个国家或地区的国民经济为描述对象,反映某一时刻社会经济各部门之间的投入产出关系②水平方向-使用情况;垂直方向-投入情况③部门总投入= 总产出
- 四个象限(从左上顺时针):1-中间消耗关系矩阵/中间流量矩阵;2-最终需求矩阵;3-最初投入矩阵/增加值矩阵;4-再分配象限
第4讲 环境系统和定量研究Ⅳ(戴翰程,20191010)
- 辐射强迫:辐射强迫是指由于气候系统内部变化,如二氧化碳浓度或太阳辐射的变化等外部强迫引起的对流层顶垂直方向上的净辐射变化。单位为W/m3。目前的辐射强迫值是2005年相对于工业化前即1750年的差值。辐射强迫是对某个因子改变地球-大气系统射入和逸出能量平衡影响程度的一种度量,同时也是一种指数,反映了该因子在潜在气候变化机制中的重要性。正强迫使地球表面增暖,负强迫则使其降温。
- 全球升温效应:
- 假如覆盖南极、格陵兰岛冰川等地的层全部融化,海平面会上升近70米,淹没绝大部分的沿海城市(即人口最集中、 繁荣最发达的区域)。
- 风暴:热带-区分布和频率不会变化,但更具破坏性;热带以外-风暴会更强烈。
- 降雨:有些地方更干,有些更湿;有些地方冬季更湿润、夏季更干旱
- 海洋酸化:大气中CO2越高,海洋中的CO2也会更多→酸化;对含碳酸钙生物不利,如珊瑚礁
- GHG增长驱动力分析—KAYA公式:排放=人口×(GDP/人口)×(能源/GDP)×(排放/能源)
- 分部门主要减排措施:
- 能源供应部门:核电、可再生能源发电、高效天然气联合循环发电或热电联产、二氧化碳的捕获和封存(CCS)技术、生物质能联合CCS 发电技术 (BECCS)
- 交通部门:开发替代新能源、改进燃烧技术提高燃料利用率、船舶和航空碳减排技术
- 建筑部门:低碳建筑,包括高性能建筑围护结构、高效暖通空调系统、高效水加热系统、高效家用电器照明以及无CO2排放技术(氢燃料电池热电联产技术)
- 工业部门:能源高效利用、提髙原材料使用效率、生物质燃料和替代原料利用以及废弃物回收利用
- 减排成本
- 减排需要成本,因其迫使消费者用更昂贵的能源。很难估算气候政策成本(原因:需要反事实的假设,需要情景对比;需要模型,需要事前政策分析;成本估算相差很大)
- 影响因素:以下情况会使全社减排成本更高(减排手段不足;减排措施成本假设过高;减排措施市场普及太慢;技术学习成本对气候政策无响应;整体经济缺乏响应,如弹性过低或资本更耐久)
- 四个原因要求减排应该是渐进式的(资本存货周转-行为和技术受耐用消费品和资本的约束;技术进步-碳中性仍不成熟且较贵;贴现率-未来的成本要贴现;碳循环-2015年的排放会降解)
- 政策工具:
- 直接管制(不适于温室气体):针对投入~能源效率标准;针对技术~触媒转化器(去除汽车尾气)~最佳实践方法+最佳可得技术(兼具费效性);针对产出~产品(致癌玩具)+废弃物(SO2排放);针对时间~空中管制;针对地点~自然保护区;禁令~氯氟烃。
- 基于市场的政策工具:
- 三种手段(税收:对每单位违规物质的使用、生产和排放征或罚款;补贴:针对不使用、生产和排放每单位违规物质的货币奖励;排污权交易:CAP and trade, CAP and trade,交易价格~税收)
- 效果评估:(优势)没有直接拼写如何减少排放,但结果上却做到了→决定权交给了 B、 C端;短期内税收和补贴对排放有相同影响→减排效果一样;但中长期内,有不同的分配效应→一些行业萎缩与另扩张
- 成本效益比较:市场手段更具成本效益,因为所有污染者面临相同的税收、补贴或许可价格;管制手段成本效益更差,除非管制者无所不知且产业均质程度较高。
- 最优化减排政策(UNFCCC第二条):“最终目标是:根据本公约的各项有关规定,将大气中温室气体的浓度稳定在防止气候系统受到危险的人为干扰的水平上。”
- 浓度稳定:
- t时刻的浓度/储量\(s_t = (1 - \delta) S_{t - 1} + E_{t - 1}\);δ为降解率,E为排放量。储量不变时\(S_t = S_{t - 1}\),得\(S = E/\delta\)。
- 假设C由五个独立储量组成,\(S_{i, t} = (1 - \delta_i) S_{i, t - 1} + \alpha_i E_{t - 1}\),其中\(\sum_{i = 1}^{5}{\alpha_{i} = 1}\),\(\delta_i = 0\),当储量稳定时,由S=E/δ知排放E=0,所以上述政策激进。
- 成本收益分析:不存在外部成本时,总私有收益开始随排放增加,而后下降。存在外部成本时总的社会损失-净排放越多损失越大;净收益开始时随排放增加,稍后下降。
第5讲 环境研究设计及数据Ⅰ(陈琦,20191017)
1. 如何设计一项研究
- 找到一个感兴趣的领域;针对一个具体问题,产生研究想法(系统的科研训练,广泛的文献阅读);查阅前人研究结果,提出研究假设;设计研究方案并开展研究。
- 广泛了解环境(自然与人)并思考其中的问题;与时俱进(变化的星球)。
- 环境研究设计实例分析:研究领域及研究问题;研究对象;数据是如何、何时、何地获得;数据是如何被分析、数据分析中发现了何种规律;如何解释数据的规律;研究结果有何应用。
2. 环境数据的收集
- 观察:直接测量。访谈和问卷:田野调查(抽样方法)。资料收集:前两种产生数据库、文献等。
- 抽样:有代表性、抽样偏差小。
- 个体、总体、样本、抽样框架:考察对象的全体;从总体中抽取的一部分个体;目标总体中的个体列表,样本要在该列表中抽取;从总体中抽取一组个体或信息以进行分析、检验。
- 抽样方法:
- 非概率抽样:被抽取完全取决于调研者的意愿。代表性不确定,只对部分研究重要。
- 方便抽样/资源抽样:不具有从样本推断总体的功能。
- 判断抽样:不能直接对研究总体进行推断。
- 配额抽样:容易掩盖偏差。
- 滚雪球抽样:有选择偏差,不能保证代表性。
- 概率抽样:代表性与抽样方法、总体特征有关。
- 简单抽样:不均匀、统计效率低;随机数法、抽签法;随机度高。系统抽样:易产生周期性偏差、统计效率低;排序后、等距离抽样;经济性。
- 分层抽样:综合简单取样和系统取样两者优点在特定间隔内随机取样;层内差异小、层间差异大;减小采样错误但不减小偏差;简单易行、代表性好(避免抽到差的样品、保证少数重要类别)、广泛使用。整群抽样:要么整群抽取、要么整群不被抽取;群内差异大、群间差异小;群内常有趋同性;简单易行、较大规模的调查中常用。
- 多级抽样:将抽样过程分为几个阶段、结合使用上述方法中的两种或数种;具有整群抽样的简单易行的优点、在样本量相同的情况下又比整群抽样的精度高;研究总体广泛且分散;抽样误差增大、计算复杂。
- 双重抽样。捉放捉抽样。
- 非概率抽样:被抽取完全取决于调研者的意愿。代表性不确定,只对部分研究重要。
- 实际应用中常注意的几点:
- 样本的选择:误差最小化。随机误差、重复误差/系统误差、相关误差(误差的数量和方向都随着被试对象的其他特征系统地变化)。
- 样本量选择:既有条件和研究目标的取舍;功效分析;精密度分析。
- 环境变量与插值:不间断的现场采样。
- 干预和对照:对照组/控制组;小鼠实验;人体暴露实验。
- 延迟效应:注意测试和干预的时间间隔;足够的反应时间;健康终点效应。
- 环境伦理:自愿参与;告知同意;对参加者无伤害;匿名与保密。
- 知情权的博弈:环境健康研究中常遇到。该告诉参与者、调查者多少:是否告知研究假设?对照或控制?双盲——参与者和调查者都不知道研究假设和操作。
- 纵向研究:持续研究中工具的标准化;维系样本组:适当的刺激;避免资料质量因时间而受损:合理的不构成负担的调查;成本控制;回溯性研究:记忆对错/资料保存——关键性事件作为内标。
- 内标很重要:化学分析——仪器设备响应变化;实验条件、样品储存条件变化;加入内标来准确定量。
- 时空的权重:环境系统复杂;数据序列常要考虑时间、空间权重。例:飞机航测。环境系统复杂(多变量);数据序列常要考虑变量同步。
- 不同时间轴:PM2.5——分钟;相对湿度、温度——秒;数谱仪——分钟;气态挥发性有机物浓度——小时。
- 采样时差。某采样点大气中这些污染物属于同一来源,浓度应有相关性,但却看不到,为何?
3. 环境数据的分析
- 观察一组数据:在亚马逊原始雨林中测得的二氧化碳浓度。
- 时间:本地/UTC。
- 重复数据点;异常值/离群值;空白值。
- 数据预处理:数据得来不易,不能轻易删数据。
- 基本换算:单位、时间、浓度、语言等。
- 有效位数保留:仪器响应。
- 空白值(缺失数据)处理:填充(插值)、剔除。
- 异常/离群值判断及处理:仪器、问卷输入、其他操作、检测限和负值。专业知识 + 统计学方法。
- 重复数据:
- 权重(空间/时间)判断及处理。
- 多组数据同步:不同时间轴多组匹配;离散数据/连续数据。
- 时间轴换算;删掉重复数据点;剔除异常值;剔除空白值。
- 描述性分析:总体分布、总体大小和离散特征;频率分析;趋势分析;比较分析。
- 解释性分析:假设检验;相关分析;回归分析;因子分析;机理探讨——模型等。
- 数据展示方法:图(柱状图、直方图、饼图、曲线图、散点图等)、表、地图、形象化处理。
- 应用数理统计基本原理:。
| 正态分布 | 大小 | 离散 | 分布 |
|---|---|---|---|
| 是 | 算术均值 | 标准差等 | 偏峰度系数 |
| 否,可变换 | 几何均值 | 几何标准差 | |
| 否 | 中位数 | 半内四分范围 | 分位数 |
- 数据挖掘基础:时间序列;空间分布;统计特征(百分比、大小、频率等);时空变化;相关和回归分析;聚类分析(主成分分析PCA、正交因子分析PMF等;形象化的图形,更准确的描述;不同坐标系的应用)。
- 相关:相关性不等于因果性。皮尔逊、肯德尔、斯皮尔曼相关分析。
- 回归:线性(一元、多元)/非线性。是否要过零点?x、y都是测量值,误差如何考虑?
4. 大学生基本学术素养
- 作图基本要素:
- 正文中图的标题/图本身的标题。
- 内容清晰,可读。(反例)文字重叠;图例缺失;配色不清(色盲色弱);坐标轴标题缺失);字号;上下标和特殊符号(PM2.5、ug/m3)。
- 美观:图的大小;图例位置;框和网格线;坐标轴刻度疏密;线的粗细及样式选择;辅助线是否需要;字体统一;标注和坐标轴的距离;标注的有效数字;特殊图形说明;配色(个人选择)。
- 注意图的意义:折线、散点、柱状。
- 专业名词及物理意义。
- 对污染物的表述专业规范:
- 空气质量标准、AQI技术规定.pdf:上下标、非通用名词、概念(首要污染物)、单位等。
- 学习专业语言、表述准确、尽量避免口语化。
- 注意参考依据、参考文献的引用。
- “全年PM2.5浓度均在200 μg/m3以下,空气质量较好。”
- “而在十二月份到2月份有几个峰,说明此时间段发生了空气污染。”
- “有不少时间超过” “…负相关、相关性强”
第6讲 环境研究设计及数据Ⅱ(戴翰程,20191024)
1. 几个研究实例
- 面向社会经济的研究方法:分为实证研究和实验研究两种。
- 实证研究:依据基本经济学原理或实践经验,通过收集数据,开展计量或统计分析。回归分析;投入产出分析;增长核算分析;统计分析;时间序列分析等。
- 实验研究:先依据有关经济学理论建立行为方程和平衡方程(方程参数大多依据经验或校准获得),然后改变外生变量(如税收政策、能源价格等),对模型系统进行运算模拟得到结果。可计算一般均衡模型;多主体模型;技术优化模型;系统动力学模型。
- 类比:环境科学研究哪些是偏实验,哪些是偏实证?两者关系如何?
- 学术论文经典结构:IMRAD。模板:标题、引言、方法、结果、讨论、结论。
- 引言:社会背景;先行研究、国际动向;先行研究的不足;怎样克服前人的不足,本文目的、研究问题、方法。
- 方法:模型、材料;数据;情景模拟设定、实验步骤;结果解析方法。
- 结果:模拟的主要结果(按重要性排序)。
- 讨论:引言/方法/结果中没有涉及的方面;按重要性排序;结果的应用;本研究和先行研究的区别;本研究的目的是否已达成,剩余哪些部分。
- 结论:本研究的主要信息;政策应用;存在的问题。
- 钢铁行业去产能政策的绿色低碳协同效益研究:
- 问题:产能的主要制约因素有哪些?如何合理预测未来的产能规模?如何评估去产能政策的成本和效益?
- 研究目标:梳理中外产业发展经验;构建产业-环境健康模型;定量对比成本和效益。
- 情景:BL——未实施去产能政策。SL——规模替代,优先淘汰小规模新建大规模工厂。EE——能效替代,有限淘汰高能耗新建低能耗工厂。
- 结果:SL淘汰大量产能/产量,能耗和CO2排放下降明显;长期效益有限。EE相比SL效益更大;CO2减排效益是效益的最大来源。
2. 研究设计方法
- 2019年诺贝尔经济学奖:阿巴希·巴纳吉、艾丝特·杜芙若、麦可·克雷默。获奖理由:为减轻全球贫困所采取的实验性方法。
- 决定性因果和概率性因果:
- 决定性因果:“有人认为空气污染不会对呼吸系统产生危害,因为他生活在北京,但是他的呼吸系统完好无损。”
- 概率性因果:“生活在污染的空气环境中比生活在洁净的空气环境中的人患呼吸系统疾病的可能性大。”
- 理论构建:根据观察归纳理论。观察(实证层面,从观察开始)\(\ce{->[归纳推理]}\)理论(概念抽象层面)。
- 理论检验:根据理论推出假设。
- 研究的一些术语:
- 因变量(左手变量):因果里面的“果”。
- 自变量(右手变量)。
- 中介变量:在因果链条中介于自变量和因变量之间。
- 外部变量。
- 建立竞争性的假设:
- 现象:私立学校的学生学业成绩比公立学校的学生的学业成绩好。
- 解释1:学习能力强的孩子选择了私立学校,而学习能力弱的孩子选择了公立学校;学习能力强的孩子比学习能力弱的孩子学习成绩好。
- 解释2:家庭背景是影响因素。
- 解释3:教育价值理念是影响因素。
- 其他解释:可能是变量测量和数据收集方面的原因,可能是一个偶然的发现,并不是普遍的现象。
- 竞争性解释从哪里来?
- 理论方面:理论;其他研究者发表的论文;实践者;统计分析;经验、直觉、灵感。
- 间接因果关系指原因变量通过其他变量对结果变量产生影响:测量方面的问题;数据分析方面的问题。
2.1. 因果关系与研究设计原理
- 因果模式的类型:任何两个变量之间的关系。
- 直接因果关系:指原因直接影响结果,而不需要通过其他的变量。
- 间接因果关系:原因变量通过其他变量对结果变量产生影响。
- 虚假关系:不是因果关系。
- 比较的逻辑:任何两个变量之间的关系。
- 对于检验因果模型而言,比较的逻辑是根本性的。
- 只有通过比较,才能排除替代性解释,才能使我们的观察有意义。
- 在设计一个解释性研究中,核心要素就是提供一个可比较的参考架构。
- 组间比较;时间点比较;进行有意义的比较;干预和自变量。
- 组间比较:二分类变量。
- 例1:离婚导致孩子的情感问题 → 发现很多父母离婚的孩子有情感问题 → 离婚家庭孩子比完整家庭孩子更容易出现情感问题(父母婚姻状况 → 情感问题的程度)。
- 例2:私立学校的学生比其他学生有更好的学业表现 → 有很多私立学校的学生取得较好学业表现的例子 → 私立学校比公立学校学生有更好的学业表现(学校类型 → 学业表现水平)。
- 例3:青年失业导致他们自杀 → 自杀的青年中有50%是失业的 → 失业的青年比有职业的青年更容易自杀(雇用状况 → 高自杀率)。
- 多重组别比较:自变量有两个以上类别。
- 例4:(上述例1)在检验离婚对孩子的影响时,也可以分为单身(从未结过婚)、完整家庭、分居、鳏寡、离婚(再婚)、离婚(未再婚)。
- 组间比较:不同变量的联合影响。
- 例5:年轻男性的自杀的可能性最高 → 比较年轻/年长、男性/女性。
- 时间点比较:
- 例6:(上述例1)假定是离婚导致了这种差异,但是在组间(离婚和完整家庭)进行简单的比较的问题在于:
- 它无法告诉我们离婚是否真的改变了孩子的情感适应性。
- 如果我们能追踪父母离婚前后孩子的情感适应性状况,看看父母离婚后孩子的情感适应性是否发生了变化,就能得出更信服的结论。
- 前测:研究之初对孩子情感适应性进行测量。
- 干预/处理(关键性事件):父母离婚。
- 后测:父母离婚后对孩子的情感适应性进行测量。
- 资料收集的时间点并非只有“前测”和“后测”,也可以有两个以上的时间点。
- 多重前测和后测有助于区分短期和长期趋势,也有助于确定“干预”或自变量。
- 例6:(上述例1)假定是离婚导致了这种差异,但是在组间(离婚和完整家庭)进行简单的比较的问题在于:
- 进行有意义的比较:
- 例7:(上述例2)除了自变量,理想的比较组在其他相关方面应该是相同的。
- 如果要检验私立学校学生比公立学校学生学习成绩更好的观点,那就必 须先确认这两组学生具有可比性。
- 由此,我们才能确定两组学生唯一的不同就是其所属学校的类型。如果他们在其他方还有差异,那又怎么知道学习成绩的差异是由什么造成的呢?
- 既然比较是一个优秀的研究设计的核心,就必须确保比较是有意义的。组间那些非预期的、不知道的差异消除的越多,就越能降低误将虚假关系当作因果关系的风险,即越能排除竞争性解释。
- 四种策略可以使增强组间的可比性:配对;随机分组;配对的区块设计;统计控制。
- 配对:在选择组员时,可以按照相关特征严谨地进行配对。
- 确保两组学生在智力、抱负、父母资源、教育价值观、家族史、性别、年龄等方面是相同的 → 就能将学校类型对学习成绩的影响分离出来。
- 事后配对缺点:信息有限,剩下的理想配对样本会很少。
- 随机分组:
- 一种比较简单却更有效地使各组具有可比性的方法,是在研究之初就随机地将人们分配到不同的组。
- 随机分组使各组间的差异是随机型的,不是系统的,只要各组足够大, 随机分配就会自动产生在已知和未知方面都相同的组。
- 参阅教材:配对的区块设计、统计控制。
- 例7:(上述例2)除了自变量,理想的比较组在其他相关方面应该是相同的。
2.2. 实验设计
- 研究设计:
- 准备工作:
- 识别研究问题(能提出一个好的研究问题至关重要,问题意识)。
- 提出竞争性假设(和研究设计的内部效度有关)。
- 进行操作化处理(和变量测量的效度、信度有关)。
- 经典实验设计:
- 两个变量:因变量(结果)、自变量(原因/干预)。
- 设计的目的:消除其他变量的影响,以便清楚地得到干预的效果。
- 例:大气中PM2.5浓度越高,人们患上呼吸道疾病的可能性越大。
- 准备工作:
- 经典实验设计:
- 这项研究的经典实验须履行以下步骤:
- 将人们随机分成两组:实验组和控制组。
- 对所有实验参与人员的上呼吸道系统状况进行测量。
- 将实验组人员暴露在PM2.5浓度超标的环境中(c超),而将控制组人员置于PM2.5浓度达标的环境中(c达)。
- 实验组暴露结束后,同时测量实验组和控制组的人员的上呼吸道系统疾病状况。
- 计算实验组人员在暴露前后呼吸系统疾病的变化状况,以及控制组在t1和t2这两个时间点的呼吸系统疾病变化状况。
- 比较实验组和控制组变化的差异。
- 这项研究的经典实验须履行以下步骤:
- 开始暴露前,两组患呼吸系统疾病的的状况一样(随机分组的结果)。
- 实验组患呼吸系统疾病的人数增多,控制组患病人数也增了一些。
- 实验组的一些变化是不能由暴露超标PM2.5环境解释的。
- 实验组的变化比控制组的变化大。
- 该实验设计基于下述两个条件:
- 暴露前,两个组在各个方面都是相同的 → 从时间1到时间2,除了特殊的干预或者处理,两个组经历了相同的事件。
- 控制组患呼吸系统疾病的人数也增了一些。
- 如果两个条件中任何一个不能得到满足,那么就存在貌似有道理的替代假设,能够解释实验组和控制组变化的差异。
- 这项研究的经典实验须履行以下步骤:
- 实验环境:实验设计可以用三种不同的方式来实现。
- 实验室实验: 可以确保除实验干预外,实验组和控制组处在完全相同的环境下。
- 田野实验: 在真实世界中开展的实验设计,真实的生活环境被当作实验室。
- 自然实验: 依赖自然发生的事件作为干预,而不是依赖实验者引入的干预。
- 赌博合法化对家庭幸福的影响。
- 扑克机合法化前后测量家庭幸福。在赌博尚未合法化的地区找一个对照组来测量家庭幸福。
- 简单的实验设计:在很多环境里,我们并不能得到经典实验要求的所有测量(实验组合控制组的前测和后测)。在某些环境下,没有这些测量也能得出有效的推论。
- 单控制组后测设计:只要小组足够大,随机分配的实验组和控制组意味着实验组和控制组之间的任何差异都是随机的,并不会导致结果变量的组件差异。因此,当我们按照随机方法划分小组时,可以省略前测阶段。
- 回溯性实验设计:自然实验的问题在于:由于这种小组不是通过随机选择形成的,任何小组之间的差异可能仅仅反映了“干预前”的差异。回溯性设计是在“实验干预”之后构造实验组和控制组,可以在两个方面改进自然实验设计。
- 更复杂的实验设计:
- 多重后测:由于干预效果可能不会立即显示或者只能维持一个很短的时间,多重后测有助于辨别短期和长期效果。
- 多组:干预经常是多种形态的,可能有很多可供选择的干预用来评估(强制投票对选举出席人数的影响)。
- 所罗门四组设计:干实验中存在一个问题,当有前测和后测阶段时, 即使没有任何的干预,这些测量本身可能也会让测量对象产生一些变化,这就是所谓的工具反应。所罗门四组设计有助于评估变量结果是不是由工具反应导致的。
- 实验设计的优缺点:
- 优点:使我们辨认出一个变量具有何种程度的直接因果效应。实验的优势通过随机化获得,但是随机化使得确定其他因素的效应变得困难。
- 缺点:低估间接因果效应,导致低估总的因果效应。随机化在提供了隔离实验变量效应的同时,也妨碍我们去检验更加复杂的因果模型或者得出干预为什么会产生影响。
- 综合:实验设计可以识别什么样的干预有影响,但不能帮助我们识别为什么这个干预有影响。
- 内部和外部效度:
- 所有的设计都面临内部效度问题。
- 如果在前测和后测之间发生了某些事件,那么这些事件就可能对实验的内部效度产生影响,尤其对于自然实验和田野实验。
- 实验设计通过控制组来处理这种问题,只要控制组和实验组经历了同样的不被控制的外部事件,那么实验干预仍然是组与组之间的唯一差别。外部事件的发生意味着我们不能把我们所观察到的变化都归因于实验干预,但我们仍然可以将实验组和控制组的变化量差异归因于实验干预效应。
- 但是,即使使用了控制组,那些未受控制的外部影响也仍然会产生问题。我们不能保证,实验组和控制组所经历的未知且未受控制的外部因素的影响是相同的。
- 一些变化量是由于时间的流逝而非实验干预所引起的。(如教学方法对孩子数学成绩的影响,需要保证他们成绩的任何变化都是由于实验干预(教学方法)引起的,而不是因为他们长大了一些)。
- 外部效度问题:
- 定义:指在多大程度上能将实验研究结果从样本推论到其代表的总体。
- 前测的反应效果;非代表性。
- 所有的设计都面临内部效度问题。
2.3. 纵向设计
- 纵向(研究)设计:
- 例子:2000年以来北京大气污染状况和居民患呼吸系统疾病状况之间关系的变化。
- 特点:纵向设计关注变量或者变量之间的关系随时间的变化,并通过收集至少两个时间点上的数据来完成这一目标。
- 特点:纵向设计可以用来回答描述性的问题,也可以用来回答解释性的问题。
- 纵向设计的目的:
- 描述变化模式:北京居民的环境意识随时间的变化状况;每隔几年进行的人口普查。
- 建立时间顺序,便于因果分析。
- 确立成长(年龄)效应/历史(时期)效应。
- 现象:年龄与政治保守主义的关系:老年人\(\gg\)青年人。
- 可能原因1:人们随着年龄的增长而变得保守?他们可能变得更没有冒险精神,需要更大的确定性,或者对那些宣称变化会使世界变得更美好的人持更加怀疑的态度。
- 可能原因2:这种相关关系反映了老年人成长并形成政治观点的那个年代?如,大萧条时期成长起来的一代人有着经济上没有保障的经历,这可能是他们在政治上趋于保守的原因。
- 分析方法:确定保守主义是否为成长的结果,唯一可信的方法是在一段时期内追踪相同的个体,看看他们是否随着年龄的增长而发生变化。
- 不考虑历史时间或时期的作用,每个特定年纪的人都有一个特定的保守水平。而且,所有的同期群显示了相似的变化度,这种变化与特定的历史时期无关。
- 政治保守程度是由人们何时出生决定的,对于不同年龄组的人,他们保守性的差别是由于历史效应而不是因为有的人年龄大造成的。
- 生命历程生涯分析。
- 简单前瞻性追踪调查设计:
- 测量:收集相同样本在两个时点上的数据。
- 干预:可以选择积极介入,或仅观察时间1和时间2之间自然发生的影响。
- 和经典实验设计的区别:缺少随机控制组。
- 存在问题:无法知道变化是由研究者的“干预”,还是时间逝去或其他影响引起。
- 多重时间点前瞻性追踪调查设计:
- 测量:和简单的两点设计相似,但是需要在更多的时间点收集数据。
- 干预:可能在收集数据的不同点上施加特殊的干预,或者简单地收集每个测量点之间相关干预事件的信息。
- 目的:缺少随机控制组。
- 测量:考察长期和短期效应。
- 干预:追踪什么时候发生变化的。
- 目的:描述变化的曲线形状。
- 目的:识别变化(或无变化)前的因素。
- 到目前为止的所有设计都涉及了在一段时间内追踪一组样本。
- 优点:可以帮我们确定时间发生的顺序,从而使我们能够构造强有力的因果顺序和因果解释。
- 缺点:费用太高、样本流失、在收集关于样本变化的有用资料时存在滞后。
- 缺点:有些研究,通过在一个时点上收集所有信息来重现跨时间的数据是可能的。通过要求人们回忆发生了什么,以及何时发生,我们可能重构变化的水平和事件的顺序。
- 回溯性调查设计。
- 记录连接设计:
- 这种设计的数据往往从官方记录获得,数据记录是跨时间收集的,因此我们可以建立一个事件的时间序列。
- 为进行这种设计,在记录上需要有个人的标识符,这样我们才能保证连接的是同一个人的跨时间记录。
- 这种记录的例子包括:报税、社会保障记录、医疗记录、犯罪记录等等。
- 在进行纵向设计时,需要做出多个重要决定,这些决定确定了纵向设计的类型
- 是否要追踪同一个个案:
- 趋势研究:重复的截面研究,在不同的时间收集可以进行比较的样本的信息,但是没有必要针对同一人群。
- 追踪调查:对同一人人群进行重复调查,这中设计可以追踪整体水平和个体水平上的变化(例:纪录片《56up》)。
- 是否需要在同一时点上收集数据:
- 前瞻性研究。
- 回溯性研究。
- 纵向设计的其他方面:
- 场合:实验室、小规模的群体、大范围的全国调查。
- 时间范围:非常短到很多年。
- 时点个数。
- 计划间隔。
- 是否要追踪同一个个案:
2.4. 截面设计
- 问卷特点:
- 无时间维度。
- 着眼于既存的差异,不引入干预。
- 根据既存的差异而非随机分配来分组。
- 只能用来测量组间差异,而不能用来测量前后变化。
- 截面设计特点:
- 截面设计和实验设计都考察因变量的变化和自变量的变化是否存在系统性的联系来解释因变量的变化。
- 截面设计采用比较消极的方法来建立因果推论,而实验是积极地去创造自变量的变化。
- 截面设计:无时间维度。
- 截面设计数据是在同一时间点收集,追踪调查设计和实验设计在不同的时间点收集数据。所以,截面设计能用来测量组间差异,而不能用来测量前后变化。
- 测量差异与测量变化:(例:考察孩子对婚姻幸福的影响)
- 可追踪调查设计:根据因变量的不同变化量来进行组间比较。
- 截面设计:仅仅是根据变量的不同来进行组间比较。
- 截面设计中“组”的性质:
- 依赖于组间比较,个体是随机分配到各组的。
- 在引入实验前,两组应该是相同的。通过控制干预因素,研究者积极地创造组间差异,在实验设计中,这一干预因素就是自变量。
- 这一区别性对待是各组间唯一的差异,因此各组在结果变量上的差异都应该归因于它。
- 在截面设计中,各组是根据样本的的既存差异来建构的。样本根据它们碰巧所属的自变量分别被划分成各个研究组。
- 由于截面设计依赖于既存差异,所以不能采用随机分配来形成各个研究组。各组除了在他们所属的自变量类别方面存在不同之外,在其他方面可能也有差异。这就使得我们很难确定组间在结果上的差异究竟是由自变量引起的,还是由组间的其他差异引起的。
- 重复截面设计:
- 截面设计常常由于缺乏事件维度而受到质疑,由于这一缺陷,截面设计不能明确地确立事件之间的时间顺序。
- 重复截面设计可以将这个问题控制在一定范围内:在不同的时点收集数据,每一个时点选择的样本是不同的。
- 重复截面设计和追踪调查:
- 趋势研究(重复的截面研究):在不同的时间收集可以进行比较的样本的信息,但是没有必要针对同一人群。
- 追踪调查:对同一人群进行重复调查,这中设计可以追踪整体水平和个体水平上的变化。
- 截面设计的优缺点:
- 优点:
- 能使研究者相对快捷地获得研究结果。
- 由于是在同一时点收集数据,在分析数据之前没有必要考虑后续阶段和干预变量。
- 在其他方面相同的情况下(如样本规模、总体、样本类型),截面设计也比对比实验设计和纵向设计的成本效率更高。
- 截面调查是获得描述性信息的最理想的方式,但是截面设计并不局限于描述性分析。采用统计控制的分析可以使截面数据提供有关因果过程和检验因果模型的有用信息。
- 缺点:
- 不具有时间维度,与追踪调查设计和实验设计有区别。
- 很难确定事件的时间顺序,很难确定因果方向。
- 由于着眼于既存差异而非随机分配,自变量的任何显著效应都可能是由其他未控制的组间差异引起的。
- 优点:
- 内部效度:
- 当研究设计的原理和结构不能帮助我们在多个对结果的解释中做出明确选择时,我们就遇到了内部效度问题。
- 大多数威胁(历史变迁、人的成长、测量工具失效、统计回归、损失率、测试影响)都是由于这些设计中具有历时性因素。
- 截面设计不会有这些问题,截面设计中的内部效度主要由于缺乏时间维度而很难确定因果关系。
- 应对方法:
- 确立因果关系和控制混淆变量。
- 统计控制:运用统计方法消除组与组之间的差异,使各组尽可能相同,我们需要知道当其他条件相同时,X的变化能导致Y发生多大变化。
3. 数据分析
- 数据:一组事实。
- 社会科学数据(经验观察)是关于人类行为领域的事实。
- 事实不会自己说话,数据分析的任务是试图赋予这些事实以意义。
- 涉及对统计工具的系统运用。
- 数据从哪里来?实验室;观测/监测;文献中;调研访谈;统计数据;模型模拟等等。
3.1. 统计分析——多元回归
- 测量:在任何假设之前,调查的变量必须被测量。
- 因变量y:学术能力,满分是100分。
- 自变量x:影响成绩的几个可能因素:父母的教育;学生冬季;其他变量(导师评价、宗教、性别、社区类型等)。
- 纳入多个自变量,理由有二:
- 假定因变量y受多个因素影响。
- 希望增加x影响y这一诊断的信心,即使在考虑了其他因素之后。
- 多元回归模型的一般形式:\(y = a + b_1x_1 + b_2x_2 + \cdots + b_kx_k + e\)。
- 其中:y是因变量;x1、x2、…、xk是自变量;a是截距估计值;bi是斜率估计值,意思是当控制其他条件不变的情况下,当xi变化时y会发生什么情况;e是误差项。
- 通过最小二乘法可以得到最佳线性拟合。
- 与简单回归不同,该拟合不是二维空间的直线,而是k + 1维空间的一个高维平面。
- 我们不相信成绩仅受父母影响,其他因素也会影响学生成绩,如社区类型,并猜测农村学生成绩比城市学生成绩高。构建模型:\(y = a + b_1x_1 + b_2x_2 + e\)。
- 其中:y是成绩;x1是父母受教育年数;x2是社区类型(0 = 城市,1 = 农村)。
- 模型估计是:\(y = 5.46 + 4.44 x_1 + 11.28 x_2 + e\),t值:(0.79)、(8.69)、(3.99),r2 = 0.72,n = 50。
- 解读1:b2 = 11.28,t值远大于2,所以可以肯定:该变量对学生的成绩有影响。
- 解读2:如果保持x1不变,农村学生的考试分数大约比城市高11分。
- 解读3:父母教育x1的作用也是统计显著,每增加一年,分数提高4.44分,比一元回归值(5.04)略小,但更为准确,因为引入了控制,即通过保持x2不变实现的。
- 解读4:多元模型比一元模型拟合更好,因为r2增加了0.09(从0.63到0.72)。
- 在多元回归中,如何实现统计控制极其重要。
- 对于观测数据来说,一般不会考虑干预自变量取值这一做法。
- 研究的社会、政治或心理因素都不受研究者直接影响,而采取非实验的方法。
- 在技术上,多元回归如何做到这一点?
- 问题:模型是否纳入了正确的变量?
- 除了统计结果之外,理论和前人研究具有重要指导作用。
- 如果需要其他变量,他们被测量了吗?。
- 不纳入这些变量的代价是什么?。
- 试验:纳入学生动机x3,学生自己越努力,成绩越好。
- 模型估计是:\(y = 5.4 + 4.46 x_1 + 11.3 x_2 - 0.1 x_3 + e\)。
- 解读1:学生动机变量并未得到支持,x3值是负数,且t值只有0.05,远达不到统计显著要求。
- 解读2:其他变量的系数和相应统计量和二元模型比没什么变化。
- 延伸1:即使纳入导师评价这一变量,其t值也在0.05水平上统计不显著。
- 我们相信原来的x1和x2模型是真实的,经受住了纳入其他已经测量变量的挑战。
- 但对那些没有纳入或没有测量的自变量又如何呢,如高中平均绩点或出勤情况。 它们没有测量,故被归入了方程的误差项。
- 简单回归与报告回归结果关键指标。有变量、测试、系数、显著性检验、拟合优度、样本信息等。
第7讲 环境研究建模实例Ⅰ(戴翰程,20191031)
- 中国生产碳排放大于消费引起的碳排放
- 投入产出方法是研究和分析国民经济各个部门在生产和消耗之间数量依存关系的一种方法
- 一个部门的变化会通过供应链影响到其他部门
- 投入:一个系统进行某项活动过程中的消耗;中间投入:生产过程中对各部门产出的消耗,如材料、动力等;初始投入:生产过程中对初始要素的消耗,如固定资产、劳动、土地
- 产出:一个系统进行某项活动过程的结果
- 系统进行各项活动的投入与产出之间具有一定的数量规律性
- 中间需求/中间产品/中间使用:本时期在本系统内需进一步加工的产品
- 最终需求/最终产品/最终使用:本时期在本系统内已经最终加工完毕的产品
- 投入产出表:以一个国家或地区的国民经济为描述对象,反映某一时刻社会经济个部门之间的投入产出关系,水平方向使用情况,垂直方向投入情况,部门总投入=总产出
| 中间需求Z | 最终需求Y | 总产出X | |
|---|---|---|---|
| 中间投入 | 中间消耗关系矩阵/中间流量矩阵 | 最终需求矩阵-消费,资本形成,净出口 | |
| 最初投入V,M | 最初投入矩阵/增加值矩阵-固定资产折旧、从业人员报酬、生产税净额、营业盈余 | 再分配 | |
| 总投入 |
- 中间需求+最终需求=总产出,中间投入+最初投入=总投入,全社会最终需求合计=全社会增加值合计
- \(a_{ij} = z_{ij} / x_{j} > 0\):第j部门生产单位产品对第i部门产品的直接消耗量,列和小于1
- 直接消耗系数(技术系数/投入系数)反应一定技术水平下第j部门与第i部门间的技术经济联系,影响因素有技术水平、管理水平、部门内部产品结构、价格、需求与生产能力的利用程度
- AX+Y=X,Y=(I-A)X:I-A的列体现单位实物产品中的投入产出关系,负为投入,每一列说明为生产一个单位产品需要投入的产品,对角线为除去自身消耗的净产出
- 列昂惕夫逆矩阵/完全需求系数矩阵\((I-A)^{-1}\):\(X = (I-A)^{-1}Y\),揭示国民经济各部门之间经济关联关系,\(I_{ij}\)表示j部门生产单位最终产品对i产品的完全需求量,是对总产品的需求,各列表现当最终需求增加1单位时经济部门产生的直接和间接波及效应
- 完全消耗系数=直接消耗系数+全部间接消耗系数:j产品部门增加1单位最终产品对i产品的直接消耗和间接消耗总量,\(b_{ij}\)
- N次间接消耗系数:\(A_{n-1}\)
- A矩阵意义:局部指标联系总量指标,微观技术定额联系宏观经济关系,揭示总产出率和最终使用量关系
- 污染物直接排放系数P=TX,Ti——第i部门单位产出排放的污染物
- 2012年中国居民消费平均碳足迹为1.7吨CO2/人。
- 碳足迹和水足迹:消费过程直接和间接产生的碳排放和水资源消耗。
- 把居民消费的碳足迹分为:住、出行、饮食货物消费 服务行、饮食货物消费服务;中国居民消费的碳足迹较低,城乡差距大
- 排放分配给产品和服务的最终消费地
- 我国碳排放增长因素:能源结构、能源强度、消费投资进出口扩张、投入产出系数,能源强度、投资扩张、出口扩张效应影响最大
第8讲 环境研究建模实例Ⅱ(陈琦,20191107)
1. 数学模型/环境体系
- 蓄水问题:\(\cfrac {\mathrm dh} {\mathrm dt} = -kh + P_0 + P_1\cos(\omega t)\),有解析解\(h(t) = \left(h_0 - \cfrac {P_0}{k} - \cfrac {P_1k}{\omega^2 + k^2}\right)\exp(-kt) + \cfrac {P_0}{k} + \cfrac {P_1[\omega\sin(\omega t) + k\cos(\omega t)]} {\omega^2 + k^2}\)。
2. 简单大气污染模型
- 空气污染的根源:能源消耗 → 一次污染控制:控制排放 → 二次污染防治难:大气活性。
- 大气污染物一维反应器模型:质量变化量 = 源 - 汇。
- 污染物大气停留时间(寿命):\(\tau = \cfrac {m} {F_{\text{out}} + L + D}\),假设为一级反应,\(m_t = m_0\exp(-kt) + \cfrac {S}{k}[1 - \exp(-kt)]\)。寿命阻抗模型:\(\cfrac {1} {\tau} = \cfrac {1} {\tau_{\text{out}}} + \cfrac {1} {\tau_c} + \cfrac {1} {\tau_d}\)。半衰期\(t_{1/2} = 0.69\tau\)。
- NO-NO2-O3光化学循环:微分方程组 → 稳态近似 → 解出浓度变化 → 加入VOC。
- EKMA曲线:光化学烟雾是控制VOC还是NOx?NOx浓度低时控制NOx浓度,高时控制VOC浓度。
- 观测VOC:塔(10+ m)、无人机(100+ m)、地面遥感/卫星(10+ km)、飞机(100+ km)。
第9讲 环境研究建模实例Ⅲ(陈琦,20191114)
1. 大气污染物
- 主要污染物及其来源:
- SO2:化石燃料、炼油、炼铜、水泥加工 → H2SO4。
- NOx:化石燃料 → HNO3。
- O3:光化学烟雾。
- 颗粒物(PM10、PM2.5、TSP):一次、二次。
- CO:化石燃料、生物质、甲烷转化、植物、海洋。
- Pb(TSP):汽油添加剂、工业。
- 苯并[a]芘(PM10):多环芳烃燃烧、尾气。
- 环境空气质量标准:算术平均值(1、8、24 h、月平均、季平均、年平均),标准状态(与实际条件、标定条件差别),数据有效性(50% ~ 75%提高至75% ~ 90%)。
- 环境空气质量标准与健康效应之间的关联:碳氧血红蛋白浓度[COHb] = β (1 - e-γt) [CO]。意识丧失、各种缺氧症状、头疼、心脏病人。
- 环境空气质量标准对比:PM2.5限值——中国15、35 μg/m3;美国12,15 μg/m3。
2. 三维大气污染模型
- 大气传输与扩散:水平传输依靠大气环流(风),垂直传输依靠浮力(对流)和湍流。
- 连续性方程:实际上是时间和空间上的微分方程。
- 欧拉模型:固定坐标系,浓度\(n(X, t)\),\(X = (x, y, z)\)。\(\cfrac {\partial n} {\partial t} = - \nabla \cdot F + P - L\),其中\(\nabla \cdot F = \cfrac {\partial F_x} {x} + \cfrac {\partial F_y} {y} + \cfrac {\partial F_z} {z}\)。考虑湍流扩散,\(\cfrac {\partial n} {\partial t} = -\nabla \cdot (nU + Kn_{\mathrm a}c) + P - L\)。
- 算子分裂法:\(n(X, t_0 + \Delta t) = CTA \cdot n(X, t_0)\),C、T、A分别时化学、湍流、对流算子。C解一阶常微分方程组。T、A网格法数值求解。
- 同时考虑随空间、时间的有限差分,计算过程易于追踪,假设三个算子在时间步长内独立,准确性取决于网格大小、时间步长、传输项和化学项求解的算法。
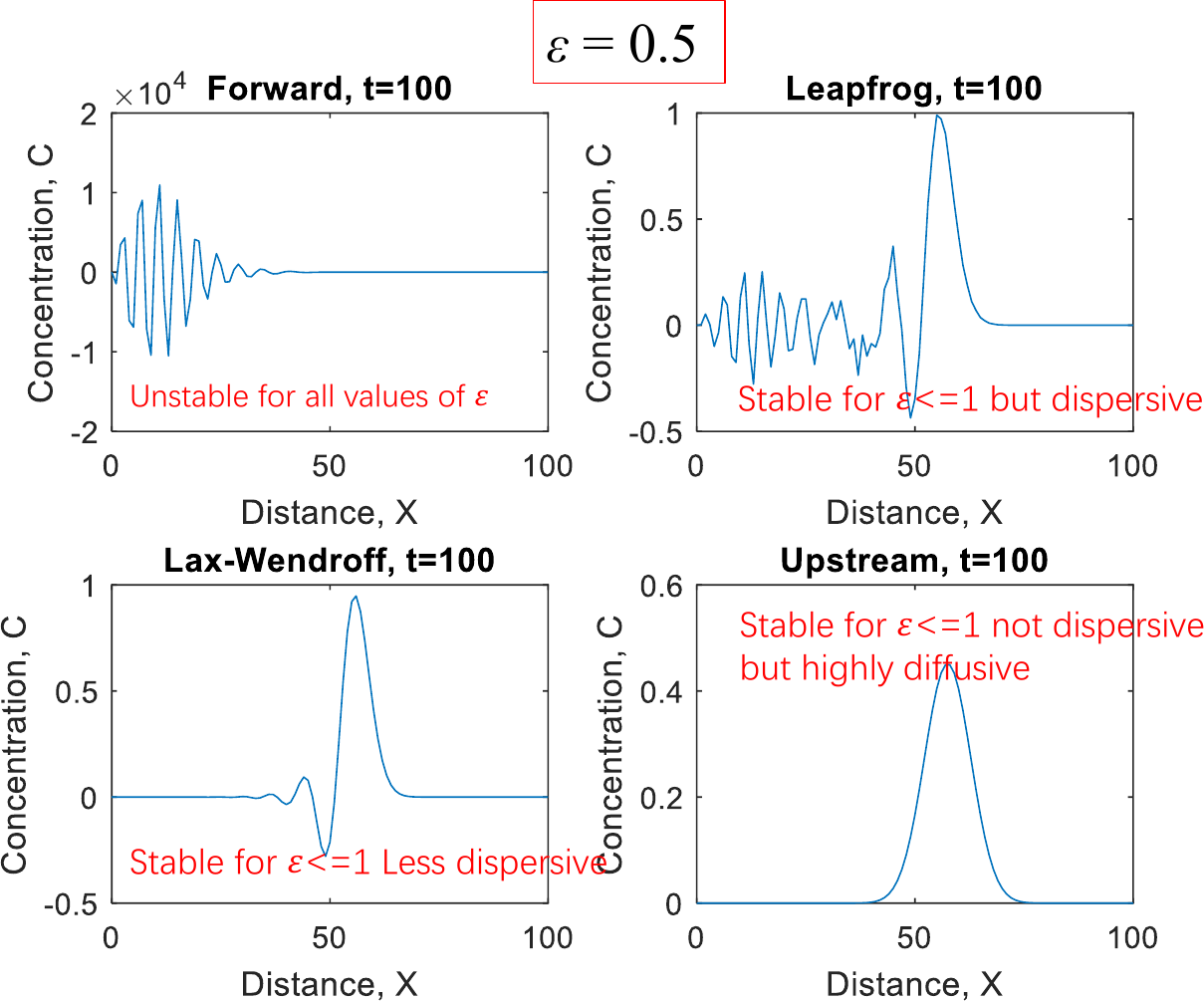
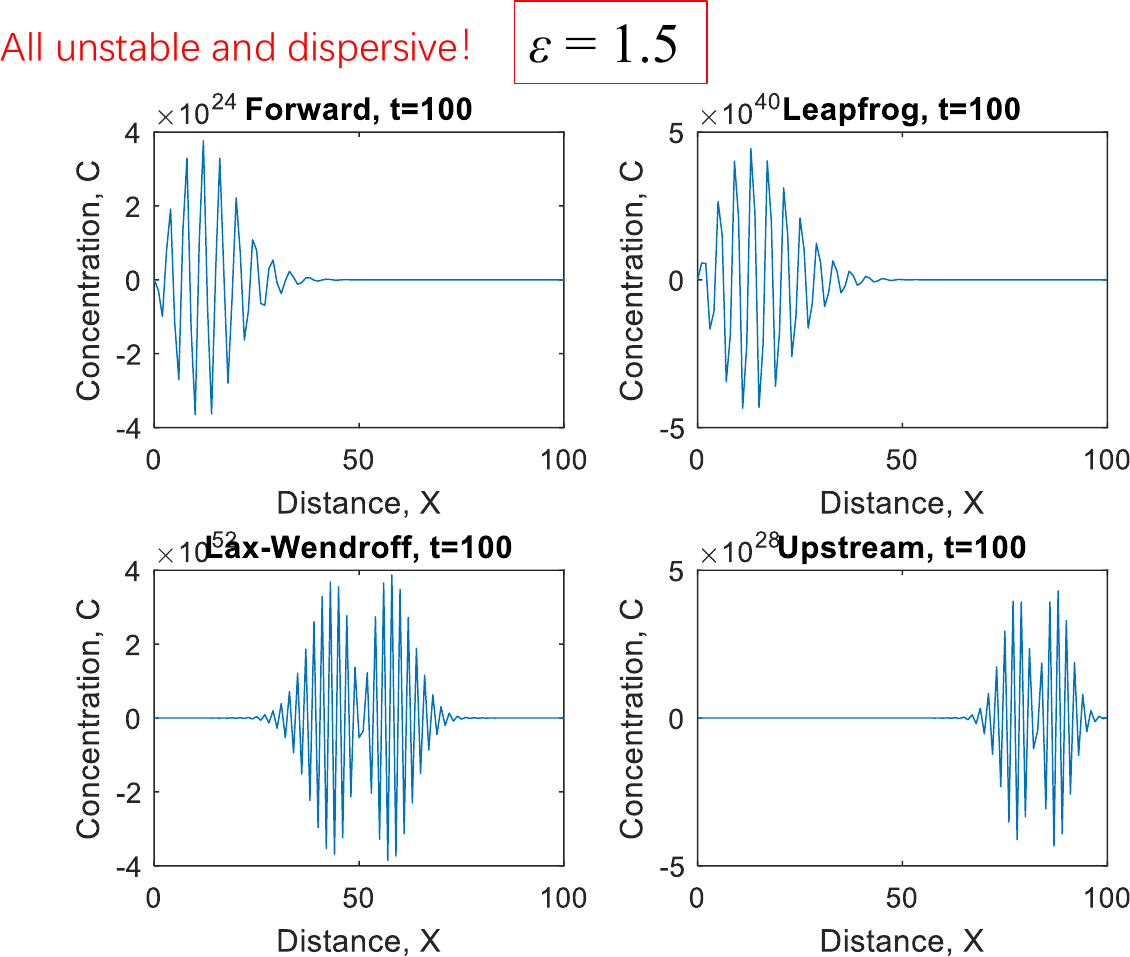
- 课堂练习:一维空间方波在x方向上的传输,考虑\(\varepsilon = 0.5\)和1.5。四种模式Forward Eulerian、Leapfrog、Lax-Wendroff、Upstream。F对所有\(\varepsilon\)均不稳定,Le、La、U对\(\varepsilon \le 1\)稳定。
- 欧拉模型:固定坐标系,浓度\(n(X, t)\),\(X = (x, y, z)\)。\(\cfrac {\partial n} {\partial t} = - \nabla \cdot F + P - L\),其中\(\nabla \cdot F = \cfrac {\partial F_x} {x} + \cfrac {\partial F_y} {y} + \cfrac {\partial F_z} {z}\)。考虑湍流扩散,\(\cfrac {\partial n} {\partial t} = -\nabla \cdot (nU + Kn_{\mathrm a}c) + P - L\)。
| 模型 | 差分方式 | 方程 |
|---|---|---|
| F | 时间正向,空间中心 | \(c_{i, t + \Delta t} = c_{i, t} + \cfrac {\varepsilon} {2} (c_{i - 1, t} - c_{i + 1, t})\) |
| Le | 时间、空间中心 | \(c_{i, t + \Delta t} = c_{i, t - \Delta t} + \varepsilon (c_{i - 1, t} - c_{i + 1, t})\) |
| La | 时间正向、空间中心 | \(c_{i, t + \Delta t} = c_{i, t} + \cfrac {\varepsilon} {2} (c_{i - 1, t} - c_{i + 1, t}) + \cfrac {\varepsilon^2} {2}(c_{i + 1, t} - 2c_{i, t} + c_{i - 1, t})\) |
| U | 时间、空间反向 | \(c_{i, t + \Delta t} = c_{i, t} - \varepsilon (c_{i + 1, t} - c_{i, t}), u \le 0\) \(c_{i, t + \Delta t} = c_{i, t} - \varepsilon (c_{i, t} - c_{i - 1, t}), u > 0\) |
-
- 拉格朗日模型:主要依据概率密度求解,无需参数化湍流,对非线性化学过程能力不足。常用在点源排放扩散(烟羽行为)。
- 考虑下垫面反射,\(C(x,y) = \cfrac{Q}{\pi u_{H}\sigma_{y}\sigma_{z}}\exp\left( \cfrac{- y^{2}}{2\sigma_{y}^{2}} \right)\left[\exp\left( \cfrac{- {(z - H)}^{2}}{2\sigma_{z}^{2}} \right) + \exp\left( \cfrac{- (z + {H)}^{2}}{2\sigma_{z}^{2}} \right)\right]\),\(\left( \cfrac{u_{H}}{u_{a}} \right) = {(\cfrac{H}{z_{a}})}^{p}\)
- 逆温影响:垂直扩散受约束(近地面逆温 → 下垫面上移,处于稳定层结构中;高空逆温 → 不能扩散到近地面,上边界多重反射)
- 线源:简化为无限长线污染源,风向与线源垂直。\(C(x, H) = \cfrac{2Q}{\sqrt{2\pi}\mu\sigma_{z}}\exp\left( \cfrac{- H^{2}}{2\sigma_{z}^{2}} \right)\)。
- 面源:多线叠加或箱式模型。\(C(t) = \left(\cfrac{QL}{\mu H} + c_{\text{in}}\right)\left[1 - \exp\left(- \cfrac{ut}{L}\right)\right] + c_0\exp\left(- \cfrac{ut}{L}\right)\)。
- 拉格朗日模型:主要依据概率密度求解,无需参数化湍流,对非线性化学过程能力不足。常用在点源排放扩散(烟羽行为)。
第10讲 环境研究建模实例Ⅳ(陈琦,20191121)
1. 温室气体模型
- 辐射强迫\(\Delta Q\):辐射强迫对应辐射平衡,对某个因子改变地球-大气系统射入和逸出能量平衡影响程度的一种度量;比较各种温室气体、气溶胶、反照率及太阳辐射变化的影响,正强迫使地球变暖。
- 辐射强迫:2011(2.29 H)、1980(1.25 H)、1950(0.57 M)。
- 气候敏感度:\(\Delta T_0 = \lambda \Delta Q\),每增加单位辐射强迫所升高的温度,基于地球是黑体。其中\(\lambda = \left[ 4(1 - f / 2)\sigma T_0^3\right]^{-1}\)。冰、水蒸气、温度递减率正反馈,云有正负反馈:\(\lambda = \lambda_{\mathrm B} + g\lambda\),其中g为反馈因子。
- 太阳辐射通量:\(S = \sigma T_{\mathrm s}^4 \cfrac {R_{\mathrm s}}{d^2} \approx \pu{1368 W/m2}\)。地球能量平衡:\(\sigma T_{\mathrm e}^4 = \cfrac {S(1 - A)} {4}\),其中A = 0.28,Te = 257 K(无大气层)。
- 基尔霍夫定律:大气近似灰体,吸收率 = 辐射率,为常数。
- 简单温室气体模型:\(f\sigma T_0^4 = 2f\sigma T_1^4\),\(\cfrac{S(1 - A)}{4} = f\sigma T_0^4 + (1 - f)\sigma T_1^4\),0为地面,1为大气。求解\(T_0 = \sqrt[4] {\cfrac {S(1 - A)} {4\sigma(1 - f/2)}}\),f = 0.74,T0 = 288 K。
- 云的作用(双层大气),人类温室气体排放(两层长波辐射吸收率增加),硫酸盐气溶胶(吸收增加,反照增加),黑碳气溶胶(吸收增加更多,反照增加),停止化石燃料(吸收增加-温室气体长寿命,PM短寿命)。
- 大气辐射传输与卫星遥感:\(I_\nu(s) = I_\nu(s_0)\exp[-\tau_\mu(s_0, s)] + \int_{s_0}^s B_\nu(T(s'))\alpha_\nu(s')\exp[-\tau_\nu(s', s)]\mathrm ds'\)。卫星测得波数为\(\nu\)的辐射强度 = 地面发出的经大气消光后到达卫星的辐射 + 各层大气发出的辐射经消光后到达卫星的辐射总和。
- 卫星遥感应用:物质能量守恒之更复杂的模型系统与卫星反演。
- 卫星探测:临边探测、星下/天底探测、掩星探测和地面遥感。
- 临边探测:红外→微波(MLS IMG MOPITT MIPAS TES HIRDLS IASI);优:测量种类多、可测小范围、可测垂直结构、日夜都可测;缺:信噪比低、水汽干扰、低水平分辨率。
- 星下探测:紫外→近红外(TOMS GOME SCIAMACHY MODIS MISR OMI OCO);优:对低对流层敏感、可测小范围;缺:只能在白天测量,只能测量垂直柱方向;平流层干扰。
- 掩星探测:紫外→近红外(SAGE POAM GOMOS);优:高信噪比、可测垂直结构(切点);缺:由太阳决定、覆盖范围有限、低水平分辨率。
- 地面遥感:紫外→近红外(LITE GLAS CALIPSO);优:高垂直分辨率(激光返回强度+时间间隔);缺:只能探测气溶胶、覆盖范围有限。
2. 水环境——溶解氧问题
- 水污染物:营养物质(氮磷铁锰,藻类繁盛),耗氧物质(降解耗氧),溶解固体盐,重金属,废热(间接影响),有害有机物(农药、VOC、内分泌干扰素EDCs、抗生素),病原菌。
- BOD5是最重要的水体有机污染程度指标,避光密封恒温
- BOD一级反应:
- 脱氧速率:\(k_{\mathrm d}L_t\),\(k_{\mathrm d} = k_{\mathrm d, 20}\theta ^ {T − 20}\)为脱氧速率常数,\(\theta = 1.047\);\(L_t = L_0\exp(-k_{\mathrm d}t)\)为废物进入河流t天后的BOD。
- 复氧速率:\(k_{\mathrm r}D\),\(k_{\mathrm r} = k_{\mathrm r, 20}\theta^{T - 20}\)为复氧速率常数,\(\theta = 1.024\);\(D = \mathrm {DO_s - DO}\)为亏氧量,DOs为饱和溶解氧,DO为实际溶解氧。
- 氧垂曲线\(\cfrac {\mathrm dD} {\mathrm dt} = k_{\mathrm d}L - k_{\mathrm r}D\),解析解\(D_t = \cfrac {k_{\mathrm d}L_0} {k_{\mathrm r} - k_{\mathrm d}}[\exp(-k_{\mathrm d}t) - \exp(-k_{\mathrm r}t)] + D_0\exp(-k_{\mathrm r}t)\),临界时间\(t_{\mathrm c} = \cfrac {1} {k_{\mathrm r} - k_{\mathrm d}} \ln \left[ \cfrac {k_{\mathrm r}} {k_{\mathrm d}} \left ( 1 - D_0 \cfrac {k_{\mathrm r} - k_{\mathrm d}} {k_{\mathrm d}L_0} \right ) \right]\)。
- kr = kd时,\(D_t = (k_{\mathrm d}tL_0 + D_0)\exp(-k_{\mathrm d}t)\),\(t_{\mathrm d} = \cfrac {1} {k_{\mathrm d}}\left(1 - \cfrac {D_0}{L_0}\right)\)。
- 点源活塞流模型PFR:废水和河水向下游流动时横断面均匀混合,假定水流方向上没有扩散;温度、光合作用、硝化作用、底泥、支流混合、多种污染源影响;临界点前T越高脱氧速率越快,溶解氧饱和值下降,复氧降低,下游更快达到临界点,临界氧亏越大。氧亏寒冷月达标温暖月不一定达标。临界溶解氧不能低于5 mg/L,曝氧不能解决问题。
第11讲 环境研究建模实例Ⅴ(戴翰程,20191128)
- 资源环境综合分析:宏观-生态足迹分析,总物流分析,系统动力分析;微观-生命周期分析。
- 生态足迹:支持一个经济体、一群人或一个人的资源消费和废弃物讲解吸收所需要的生态功能用地。
- 生态承载力:国家或区域实际具有的生态功能用地的面积。
- 生态足迹分析法:计算生态足迹和生态承载力,比较大小。
- 生态足迹计算:
- 各消费项目人均生态足迹分量\(A_n = \cfrac {C_n} {Y_n} = \cfrac {P_n + I_n - E_n} {Y_n \cdot N}\)。\(A_n\)用地面积,\(C_n\)人均消费量,\(Y_n\)每公顷用地平均生产能力,\(P_n\)生产量,\(I_n\)进口量,\(E_n\)出口量,\(N\)人口数。
- 人均生态足迹\(ef = \sum\limits_{m,n}b_mA_n\)。\(b_m\)当量因子,\(m\)为耕地、牧地、林地等。
- 地区总生态足迹\(EF = N\cdot ef\)。
- 生态承载力计算:\(ec = a_mb_my_m\),\(a_m\)人均用地面积,\(y_m\)产量因子,生产力的修正项。计算承载力通常扣除12%的生物多样性保护面积。
- 总物流分析:在统计资料的基础上全面盘点一个国家或地区某一年内各种资源的投入了和他们在各方面的支出量,与当年和前几年国内外数据对比分析。
- 总物流分析:针对多种资源,分析更多考虑投入端和支出端;物质流分析:针对一种资源,分析还强调中间环节成分。生态足迹分析针对消费者,需要扣除出口。
- 两层系统边界:所研究区域内社会经济系统与生态系统直接的连接,区域内社会经济系统与区域外之间的输入输出边界;时间边界:1年
- 总投入 = 国内资源 + 进口 + 可再生,总支出 = 国内消费 + 出口 + 国内净增 + 污染物排放 + 再生资源产出。
- 隐藏流:资源开采过程中必须开挖但没有进入市场和产品制造过程的开挖量。
- 生态包袱:为生产某种产品投入的自然资源量与该产品自身重量的差值。
- 再生资源投入比例:再生资源投入量占资源总投入量。
- 资源生产力:单位天然资源的消耗所创造的经济价值。
- 最终处置量:无法再利用和再循环,最终成为必须进行最终处置的废弃物的物质量。
- 生命周期评价方法:目的范围确定,清单分析,影响评价,总结报告(系统边界:摇篮 → 门 → 门 → 坟墓)。
- 清单分析:系统边界内所有经济过程的自然资源投入、废物、排放物。
- 影响评价:生产系统的潜在环境影响的量和重要性
- 清单分析量化:功能单元 → 过程流程图 → 单位过程 → 单元进程清单表 → 产品系统总清单表。
- 生命周期影响评估LCIA:按影响类别分类,特性描述,归一化或权重。
- 全球变暖潜力kg CO2;臭氧层破坏系数kg R11;酸雨kg SO2;富营养化kg PO43-;光化学O3产生潜势kg C2H4。
第12讲 环境研究建模实例Ⅵ(戴翰程,20191205)
- 实证研究方法:集中(均值、众数、中位数),离散(极差,集中度,标准差)。
- 异常值处理:删除,数学变换,原封不动,分别报告。
- 变量特征——定量变量:极具价值的特征之一是测量的精确度高,均值、中位数和众数都有效。
- 变量特征——定性变量:测量精确度低。定序——根据某些特性的多少对个案进行排序,而不确切说明到底“多多少” 或“少多少”,如测量心理态度和动机水平时。名义——测量某种特征的出现或不出现。
- 变量特征——集中趋势:关注变量的典型分值,把不同的观测统一起来,提供一个概要的含义。离散:关注变量分值的散布情况,提示观测相互之间的差别有多大。
- 集中趋势:均值、中位数、众数。均值更好说明。
- 定序数据——\(\tau\)相关测量:当数据不是定量数据时,需要其他相关测试:散点图不再适用于观察两个变量的相关关系。列联表取代散点图,成为评估变量关系的初步工具。对定序变量之间的关系,\(\tau\)系数是一个有用的测度。
- 名义数据——\(\lambda\)系数:名义数据缺乏定序变量“多或少”的特性:“随着X增加,Y也倾向于增加”这样的表述无意义, 但名义变量之间仍可能存在或强或弱的关系,对名义数据而言,\(\lambda\)系数是有用的测度。
- 决定系数——多元:纳入正确变量,共线性,交互,变量和误差项是否有关,是否在恰当层次对变量测量,非线性。
- 离散特征——极差、标准差\(s_x = \sqrt{\cfrac {\sum\limits_{i = 0}^n (x_i - \bar x)^2} {n - 1}}\)。
- 相关性——相关系数\(r = \cfrac {\sum \cfrac {x_i - \bar x} {s_x} \cdot \cfrac {y_i - \bar y} {s_y}} {n - 1}\)。
- 显著性检验——Z分数:\(Z - \cfrac {\bar x_i - \mu_x} {s_x}\),任何Z分数绝对值≥ 1.96的概率是5%。
- 显著性检验——t值:\(t = \cfrac {\bar x} {s_x / \sqrt{n - 1}}\)。
- 回归分析——最小二乘法:\(b = \cfrac {\sum\limits_{i = 0} ^ n (x_i - \bar x)(y_i - \bar y)} {\sum\limits_{i = 0} ^ n (x_i - \bar x)^2}\),\(a = \bar y - b\bar x\),\(r^2 = \cfrac {\text{TSS}} {\text{RSS}} = \cfrac {\sum\limits_{i = 0} ^ n (y_i - \bar y)^2} {\sum\limits_{i = 0} ^ n (\hat y_i - \bar y)^2}\)。
- 斜率显著性检验——t值:\(t_{n - 2} = \cfrac {b - \beta} {s_b}\),\(n - 2\)是自由度,\(b\)是估计斜率,\(\beta\)是总体斜率,\(s_b\)是斜率的估计标准差:\(s_b = \sqrt {\cfrac {\sum(y - \hat y)^2 / (n - 2)} {\sum(x - \bar x)^2}}\)。
- 回归分析——非线性:先用数学变换把非线性变成线性,再用最小二乘法。
- 双重差分法(DID):是计量经济学中的非实验性方法。
- 假设在\(t_1\)时期实施了政策,真实的影响:\(Y_b - Y_a\),如果仅有\(t_1\)和\(t_2\)时期的数据,被估计的影响:\(Y_{t2} - Y_{t1}\)。
- 要求两期两组的观察数据,即数据类型必须为面板数据。
- 一组样本在第一期没有受到外来政策影响,第二期受到政策影响;第二组样本在两期都没有受到政策影响。
- 通过比较两组样本在两期内的变化差异,估计政策冲击带来的真实影响。
- 基础设定:i——城市,t——时间。面板数据——在不同时期跟踪由给定个体而获取的数据集;平衡面板数据——截面成员的时间分布完全相同,且没有缺失变量数据。每个i都有相同数量的t,每个i和t各自变量的数据都没有残缺。长面板\(t \to \infty\),短面板\(i \to \infty\)。
- 干预效应 =\((Y_{t2} - Y_{t1}) - (Y_{c2} - Y_{c1})\)。
| 组别 | 变化前 | 变化后 | 差 |
|---|---|---|---|
| 政策组1 (实验组) |
\(Y_{t1}\) | \(Y_{t2}\) | \(\Delta Y_t\) |
| 无政策组2 (控制组) |
\(Y_{c1}\) | \(Y_{c2}\) | \(\Delta Y_c\) |
| 差 | \(\Delta \Delta Y = \Delta Y_t - \Delta Y_c\) |
-
- 控制组用于识别未受干预影响时可能的演变路径。在本例中,即使没有干预,Y下降了\(Y_{c2} - Y_{c1}\)。
- 关键是没有干预的情况下,两组的时间趋势是相同的。
第13讲 前沿研究方法Ⅰ(戴翰程,20191212)
1. 全球环境展望
- GEO6:全球环境展望6。
- 环境变化的驱动力:人口、城市化、经济、能效与技术、气候变化。
- PART A:全球环境状态(压力 → 状态 → 影响 → 应对):
- 大气:排放 → 大气组分及气候 → 影响 → 政策。
- 生物多样性、海洋及海岸、土地和土壤、淡水系统等。
- PART B:环境管理及政策效果评估。
- PART C:未来情景及转型路径。
- 环境变化的驱动因素(DPSIR方法):
- 到2050年,人口将达到90亿至100亿。
- 人口统计数据:富裕国家更多老年人,贫穷国家更多年轻人。
- 城市化:到2050年,60 ~ 70亿人生活在城市,20 ~ 30亿人生活在非正式定居点。
- 经济发展:需要消除贫困、消除饥饿,但需要增加消费和开采资源。
- 技术变革:例如,可以提高农业生产率,但会产生更多的废物和毒素。
- 气候变化:已经上升了1摄氏度。面临海平面上升,更频繁的干旱,更严重的极端天气。
- 环境状况——淡水:
- 公共产品和风险倍增器:通过污染和气候变化影响人类和生态系统健康。
- 疾病:140万人死于病原体污染的饮用水,23亿人无法获得安全的卫生设施。
- 抗生素和抗菌素耐药:预计将成为2050年的主要死亡原因。
- 淡水生态系统:1997年至2011年间,全球40%的湿地消失。淡水物种数量在1970年至2012年间下降了81%。
- 食物:70%的淡水用于食物生产。新技术可以显著提高农业、工业和矿业部门的用水效率。
2. 气候政策与可持续发展研究前沿
- 中国生态环境评估综述:
- 排放和驱动力:
- 区域、部门/温室气体、大气污染物。
- 人口、经济、能效与技术、政策、分部门驱动力。
- 未来排放情景和转型路径:
- 分析方法:三类模型。
- 2度和1.5度情景,各部门情景:能源、电力、终端、农林土地。
- 减排成本,转型途径,地球工程等。
- 能源系统、城市、工业、交通、建筑、农林土地。
- 可持续消费。
- 应对气候变化与可持续发展。
- 排放和驱动力:
- 政策的综合评价
- 综合评估模型(IAM):是指结合了自然气候模型和经济模型的,能够模拟能源、环境、经济系统及其相互关系并用于气候变化研究和气候政策评估的一类大规模跨学科模型。
- 分类:自上而下(一般均衡(CGE),局部均衡);自下而上(技术优化模型,系统分析模型);混合。
- IAM集成了多种人类和自然地球系统内在联系。
- IAM能提供单个学科研究无法获得的见解。
- IAM追踪复杂和高度非线性系统之间的相互作用。
- IAM为自然科学研究者提供有关人类系统的信息,例如温室气体排放、土地利用和土地覆盖。
- IAM支持国家,国际,区域和私营部门的决策。
- 过去40年的发展历程:
- 1980年代:能源-经济-气候之间的关联;预测排放和浓度。
- 1990 ~ 2000年代:能源-经济-气候之间的关联;能源、技术和减排。
- 2000年以后:减排与土地利用。
- 2015年以后:减排与可持续发展。
3. 环院的IMED模型
- Integrated Model of Energy, Environment and Economy for Sustainable Development
- 能源环境经济可持续发展综合评价模型
- SDA:从恒等式出发的结构分解方法,一般基于投入产出表。
第14讲 前沿研究方法Ⅱ(陈琦,20191219)
1. 亚马逊热带森林中的挥发性有机化合物
- 森林排放的挥发性有机化合物(VOCs)在生态系统功能、大气化学和气候变化中发挥关键作用。
- 亚马孙河是全球生物VOC排放的主要来源之一。
- 在野外研究中,已观察到在异质土地表面上测得的VOC浓度和模拟的VOC浓度之间存在差异。
- 结论:
- 基于无人机的VOC采样技术允许在所需的中间规模进行科学研究。
- 数据约束的梯度输运模型表明,VOC排放的异质性在VOC浓度差异中起关键作用。
2. 生物成因二次有机气溶胶的形成机理
- 定量,分子层面的在线气体-颗粒吸收性分配模型。
- 颗粒的元素组成:元素比显示出很大的测量模型差距,表明模型中缺少重要的化学成分。
- 颗粒相化学显示,过氧化氢化物的分解、水的去除、自由基催化的低聚是颗粒物生成的过程,产物有些类似腐殖酸类物质。
3. 二次有机气溶胶的形成量
- 定量测量 → 参数化 → 建模。
- 结果:我国冬季交通源对有机气溶胶的贡献以SOA为主(70%以上);交通源产生的有机气溶胶在总有机气溶胶中的质量占比不高(< 10%),珠三角和长三角略高于京津冀。
4. 污染/气候变化/农业/人类
- 气候变化背景下大气-水圈-生物圈相互作用。
- 空气污染/气候变化危害全球粮食安全,影响人类生存。
例题
1. 室内吸烟
(教材例1.6)室内有人吸烟,从文献中知道吸烟会释放甲醛,思考什么情况下甲醛浓度否会超过健康浓度阈值?
已知:25 ℃、1 atm下。体积500 m3,吸烟人数50人,吸烟频率2支/人/h,释放量1.4 mg/支,换气速率100 m3/h,反应速率0.4 h-1。假定屋内完全混合,室内浓度与排出空气甲醛浓度相等。眼睛受刺激的阈值0.05 ppm。
解答:\(0 - Qc + G - kcV = 0\),\(G = 50 \times 2 \times \pu{1.4 mg/h} = \pu{140 mg/h}\),\(c = \cfrac {G} {Q + kV} = \cfrac {140} {1,000 + 0.4 \times 500}~\pu{mg/m3} = \pu{0.117 mg/m3}\),\(w = \cfrac {0.117 \times 24.47} {30}~\pu{ppm} = \pu{0.095 ppm}\)。(其中\(pV = nRT\),\(R = \pu{8.314 J.mol-1.K-1}\),\(V / n = RT / p = \pu{24.47 L/mol}\)。)
2. 支流汇合后的河流污染
(教材例1.4)两河流流量为Q1 = 10.0 m3/s,Q2 = 5.0 m3/s;污染物浓度分别为c1 = 20.0 mg/L,c2 = 40.0 mg/L。假定污染物为惰性物质,并且两条河的水能够充分混合,计算下游河水中污染物的浓度。
解答:\(c_1Q_1 + c_2Q_2 - c_{\mathrm m}Q_{\mathrm m} = 0\),\(Q_{\mathrm m} = Q_1 + Q_2 = \pu{15.0 m3/s}\),\(c_{\mathrm m} = \cfrac {c_1Q_1 + c_2Q_2} {Q_{\mathrm m}} = \pu{26.7 mg/L}\)。
3. 被污染的湖泊与生物降解
(教材例1.5)两输入口流量为Q1 = 5.0 m3/s,Q2 = 0.5 m3/s;污染物浓度分别为c1 = 10.0 mg/L,c2 = 100 mg/L。流入湖泊体积为1 × 105 m3。污染物消耗速率常数为0.2 d-1,假定污染物在湖泊中完全混合,不挥发,没有其他形式增加减少,计算稳态条件下湖泊中污染物的浓度。
解答:\(c_1Q_1 + c_2Q_2 - c_{\mathrm m}Q_{\mathrm m} - kc_{\mathrm m}V = 0\),\(Q_{\mathrm m} = Q_1 + Q_2 = \pu{5.5 m3/s}\),\(c_{\mathrm m} = \cfrac {c_1Q_1 + c_2Q_2} {Q_{\mathrm m} + kV} = \pu{3.5 mg/L}\)。
4. 厂房泄漏
一厂房泄漏,体积V = 160 m3,初始浓度c0 = 29 mg/m3,安全阈值cmax = 14 mg/m3,通风率为10 m3/min,计算多久后可以进入。
解答:\(t_0 = \cfrac {V} {Q} = \pu{16 min}\),公式变形为\(t = t_0\ln\left(\cfrac {c_0}{c_{\text{max}}}\right) = \pu{11.7 min}\)。
5. 排水管道
某排水管道输入菌落数为cin = 4.5 × 105 CFU/L,流速为u = 0.75 m/s,降解速率为k = 0.23 min-1,要求输出菌落数为cout = 2,000 CFU/L,计算管道最小长度。
解答:公式变形为\(t = \ln \left( \cfrac {c_{\text{in}}} {c_\text{out}} \right) / k = \pu{23.5 min}\),长度\(L = ut = \pu{1060 m}\)。
6. 鱼类与鸟类
(教材例1.7)河流长度L = 4.75 km,捕食鱼类数量n = 10,000条/km/h,河流断面平均面积A = 20 m2,河流流量Q = 700 m3/min,鱼类浓度c = 7条/m3,计算进入海洋的鱼类浓度。
解答:鸟类捕食速度恒定,鱼类的消耗为零级。\(k = \cfrac {n} {A} = \pu{0.5只/m3/h}\),停留时间\(t = \cfrac {LA} {Q} = \pu {2.26 h}\),按活塞流反应器计算\(c = c_0 - kt = \pu{5.9 条/m3}\)。
7. 箱式模型
假定完全混合,污染物只顺着主风向扩散。若某城市h = 250 m高处有一个逆温层,城市与风垂直方向上的宽度w = 20 km,风速u = 2 m/s。CO的排放速率为Q = 60 kg/s。假设CO是惰性物质并充分混合,计算CO的浓度。
解答:假设充分混合、惰性物质 → 质量平衡式\(lwh \cfrac {\mathrm dc}{\mathrm dt} = qlw + whuc_{\text{in}} - whuc_{\text{out}}\)。假设稳态\(\cfrac {\mathrm dM}{\mathrm dt} = 0\)→ 稳态浓度\(c_{\text{ss}} = c_{\text{out}} = \cfrac {ql} {uH} + c_{\text{in}}\)。\(c(t) = \left[\cfrac {ql}{uh} + c_{\text{in}}\right]\left[1 - \exp \left(-\cfrac {ut}{L}\right)\right] + c_0\exp\left(-\cfrac {ut} {L}\right)\)。假设进入箱子的空气是洁净的 →;假设箱中初始浓度为0 →\(c(t) = \cfrac {qL}{uh} \left[1 - \exp \left(-\cfrac {ut} {L} \right)\right]\)。