《普通化学》知识点整理

第2章气体

提纲

理想气体：理想气体状态方程和气体的分压。
气体分子运动论：压力表达式，温度的物理意义，用气体分子运动论理解宏观理想气体方程。
气体分子的速率和能量分布：理解速率和能量分布的含义，记住分布具有e指数的基本形式。
实际气体和van der Waals方程：理想气体的基本假设，实际气体近似成理想气体的条件，vdW方程的形式和vdW参数的物理意义，压缩因子的表达式。

1. 理想气体定律

理想气体状态方程：$pV=nRT$。推论：$pM=\rho RT$。
使用前提：
- 气体分子间距离很大，分子间吸引力可忽略不计；
- 气体分子自身很小，分子所占体积可忽略不计。
气体分压定律：$p_{\mathrm{total}}=p_1+p_2$。
气体扩散定律：$\cfrac{t_1}{t_2}=\cfrac{v_2}{v_1}=\sqrt{\cfrac{\rho_1}{\rho_2}}=\sqrt{\cfrac{M_1}{M_2}}$。

2. 气体分子运动论

三点假设：
- 气体由大量分子组成，分子是具有一定质量的微粒。
- 气体不断地做无规则热运动，并均匀分布于整个容器空间。
- 分子运动时不断相互碰撞，同时也会撞击器壁而产生压力，这种碰撞是完全弹性的，撞击后能量没有损失。
导出结论：
- 均方根速率与温度的关系：$\overline{v^2}=\cfrac{3RT}M$。
- 理想气体分子平均动能与温度的关系：$\overline{E_k}=\cfrac32kT$。
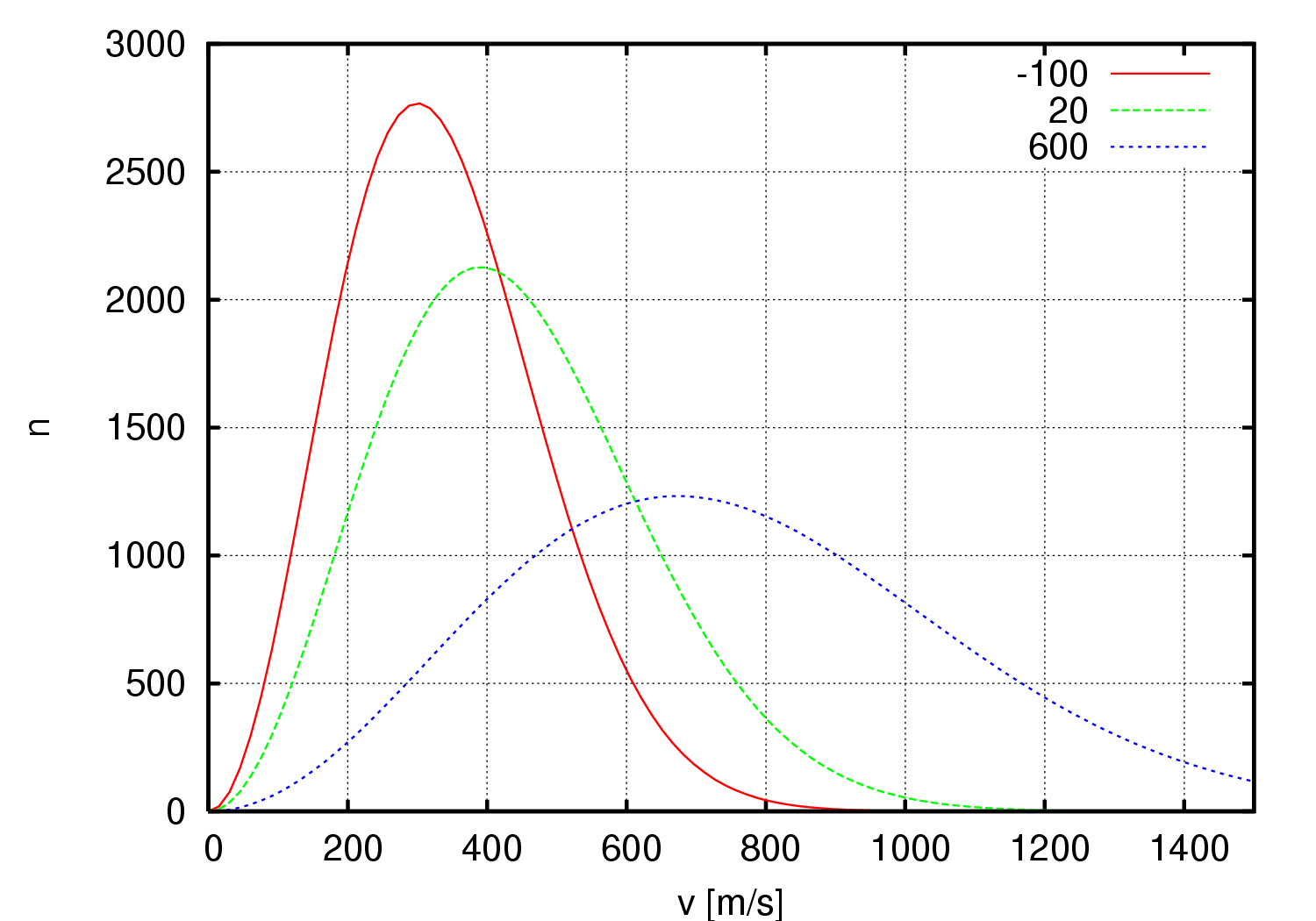
大量气体分子的行为服从Maxwell–Boltzmann分布律。

3. 实际气体和van der Waals方程

van der Waals实际气体状态方程为：$\left(p+a\cfrac{n^2}{V^2}\right)(V-nb)=nRT$。
实际气体的压缩系数$Z$：$Z=\cfrac{pV}{nRT}$。

4. 气体摩尔体积的测定

测定0 ℃时，不同压力下的气体密度$\rho$，由此计算气体摩尔体积，再计算$pV$乘积，并以它为纵坐标、$p$为横坐标作图，可得直线。将直线外延到$p\approx0$时，所得$pV$乘积，可看作是完全理想状态的数值。
也可将$\rho/p$作图，外延到$p\approx0$时求出理想状态的密度，然后代入理想气体状态方程，求未知物的分子量。

第3章相变·液态

提纲

相变：基本概念，从分子运动的角度去理解
蒸气压：基本概念，影响因素，C-C方程
单组份相图：区域、两相分界线、特殊点

1. 气体的液化·液体的蒸发

体系中的均匀部分叫做相。气体只有一相，液体、固体可以存在很多相。
临界现象：每种气体都有一个特定温度，称临界温度（$T_c$），在临界温度以上，不论加多大压力都不能使气体液化。临界现象存在的原因：单纯减少分子间距离无法克服热运动造成的扩散膨胀。
蒸发与冷凝达平衡时的蒸气分压为饱和蒸气压，简称蒸气压。蒸气压与外界气压相等时，液体沸腾。
一定温度下，蒸气压是定值，与气相和液相的量无关。
描述液体蒸气压与温度关系的公式为Clapeyron-Clausius方程：$\ln\left(\cfrac{p_2}{p_1}\right)=-\cfrac{\Delta H_{vap}}R\left(\cfrac1{T_2}-\cfrac1{T_1}\right)$，其中$\Delta H_{vap}$为液体的摩尔蒸发热。

2. 相图

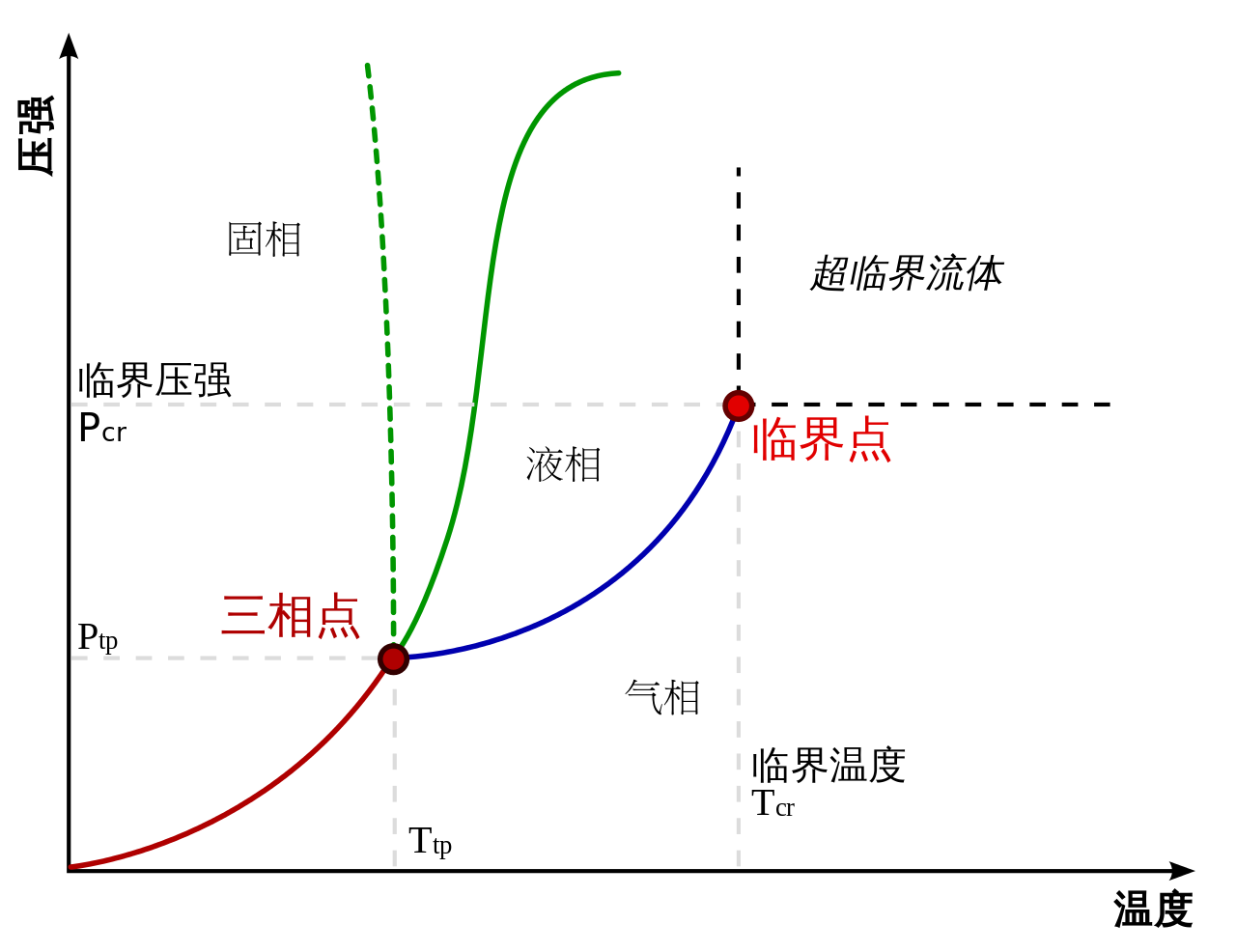
相图：表示温度、压力、组成等因素对物相影响的关系图。
在相图中，三相点代表三相共存，曲线代表两相共存，平面区域分别代表各单相区。气液线不是无限延长的，它的终点是临界点。
相图中压力的含义：对于气液、气固平衡，指蒸气压；对于固液平衡，指固体或液体表面的压力。
$\ce{CO2}$的相图固液线的倾斜方向与水不同。

第4章溶液

提纲

基本概念：溶液浓度的不同表示方法，溶解度
稀溶液的依数性：Raoult定律，凝固点下降和沸点升高，改变量正比于溶液浓度（不要求具体表达式），渗透现象和渗透压定律，几种依数性之间的关系
电解质溶液：电离理论的要点，活度和活度系数，实际溶液偏离理想溶液的原因

1. 非电解质稀溶液的依数性

蒸气压下降（Raoult定律）：溶液蒸气压的相对降低值（$\Delta p$）与溶质的摩尔分数（$x_2$）成正比，即$\Delta p=p_0x_2$。推论（$x_1$为溶剂的摩尔分数）：$p=p_0x_1$。
沸点升高：$\Delta T_{\mathrm b}=K_{\mathrm b}m$，其中$m$质量摩尔浓度，$K_{\mathrm b}=\pu{0.51K\cdot kg\cdot mol-1}$。
凝固点下降：$\Delta T_{\mathrm f}=K_{\mathrm f}m$，其中$K_{\mathrm f}=\pu{1.86K\cdot kg\cdot mol-1}$。
渗透压（$\Pi$）：$\Pi/c =$常数或$\Pi V=nRT$。

2. 电解质溶液的依数性和导电性

电解质在溶液中的电离度（$\alpha$）也可用测定电导率来计算：$\alpha=\frac\lambda{\lambda_\infty}$，其中，$\lambda$为溶液的当量电导率，$\lambda_\infty$为溶质完全电离（通常是指无限稀的溶液）的当量电导率。
20世纪初Lewis提出了有效浓度的概念，并取名为活度，定义为：$a=\gamma c$，其中，$a$为活度，$\gamma$为活度系数，$c$为溶液的实际浓度。

第5章化学热力学

提纲

热力学状态函数：$U$、$H$、$S$和$G$的定义，熵的物理意义及其影响因素，熵的宏观和微观表述，查阅热力学表格计算化学反应的$\Delta H$、$\Delta S$和$\Delta G$
两个过程参数：热力学第一定律，体积功的计算
热化学定律：Hess定律及其应用，键焓及其应用
过程：可逆与不可逆，自发与非自发，自发的判据
Gibbs-Helmholtz方程及其应用

1. 热力学状态函数的意义与关系

$U$、$H$、$S$和$G$都是状态函数。体系状态发生改变后，$\Delta U$、$\Delta H$、$\Delta S$和$\Delta G$由最终状态和起始状态决定，而与变化的路径无关。
$H=U+pV$，$\Delta H=\Delta U+p\Delta V$（恒压条件），$G=H-TS$，$\Delta G=\Delta H-T\Delta S$（恒温条件）。
内能（$U$）：根据热力学第一定律，体系内能的改变等于体系与环境之间交换的热量（$Q$）与功（$W$）的加和：$\Delta U=Q+W$。
- 当体系在等压条件下变化且只做体积功（$W_{\mathrm e}=-pV$）时，则$\Delta U=Q_p-p\Delta V$。
- 当体系在等容条件下变化且不做其他功（$W_{\mathrm e}=0$）时，则$\Delta U=Q_V$。
- 反应的等压热效应和等容热效应的关系为：$Q_p=Q_V+\Delta nRT$。
焓（$H$）：焓是一种与内能相联系的物理量，根据其热力学定义$H=U+pV$可得，在等压条件下，焓变$\Delta H=\Delta U+p\Delta V$。
- 当体系在等压条件下只做体积功时，$\Delta H=Q_p$。
- 当化学反应在恒压下进行时，反应热为恒压反应热$Q_p$。
- 一定温度下，若化学反应过程中有气体参与，且反应前后气体的物质的量变化为$\Delta n$；若将气体按理想气体处理，则有$\Delta H=\Delta U+\Delta (pV)=\Delta U+\Delta nRT$。
- 反应的等压热效应与等容热效应的关系为$Q_p=Q_V+\Delta nRT$。
熵（$S$）：熵是体系混乱度的量度。混乱度与体系中可能存在的微观状态的数目有关。可逆过程的熵变（$\mathrm dS$）可由该过程的热量（$Q_r$）除以温度得到：$\mathrm dS=Q_r/T$。
Gibbs自由能（$G$）：Gibbs自由能是从热力学第二定律出发，将$H$和$S$归并起来而得到的热力学状态函数：$G=H-TS$。在等温变化中，$\Delta G=\Delta H-T\Delta S$，（Gibbs-Helmholtz方程）。在等温等压可逆过程中，可以导出$\Delta G=W'$，即Gibbs自由能的变化等于等温等压条件下体系所能做的最大其他功。

第6章化学平衡

提纲

平衡常数表达式，利用平衡常数计算平衡浓度
标准平衡常数的计算方法、与实验平衡常数的关系
van’t Hoff等温式，$\Delta G$与$\Delta G^\ominus$，$K$与$Q$的区别与联系
多重平衡：多重平衡反应的平衡常数之间的关系
van’t Hoff方程
用Le Chatelier原理判断平衡移动方向

1. 化学平衡常数的表达

对于化学反应$\ce{aA(g) + bB(aq) <=> cC(g) + dD(aq)}$，当反应达到平衡时，生成物浓度（压力）幂的乘积与反应物浓度（压力）幂的乘积之比为化学平衡常数$K=\cfrac{[p_{\mathrm C}]^c[c_{\mathrm D}]^d}{[p_{\mathrm A}]^a[c_{\mathrm B}]^b}$。
不同表述形式的平衡常数之间的关系为：$K_p=K_c(RT)^{\Delta n}$，其中，$\Delta n$为化学反应式中生成物与反应物的计量系数之差。

2. 平衡常数与Gibbs自由能变

一定温度下，若反应在非标态下进行，此时反应的$\Delta G(T)$与$\Delta G^\ominus(T)$的关系符合van’t Hoff等温式：$\Delta G(T)=\Delta G^\ominus(T)+RT\ln Q$，其中，$Q$为反应商。
当反应达平衡时，$\Delta G(T)=0$，可得$\Delta G^\ominus(T)=-RT\ln K^\ominus$。

3. 化学平衡的移动

Le Chatelier原理：当处于平衡状态的体系的某一物理量发生改变时，体系总是要向着使这种改变减小的方向移动。
温度对反应方向的影响：$\ln K=-\cfrac{\Delta H^\ominus(T)}{RT}+\cfrac{\Delta S^\ominus(T)}R$。当焓变和熵变随温度变化不大时，平衡常数与温度的关系可以表示为：$\ln\left(\cfrac{K_2}{K_1}\right)=\cfrac{\Delta H^\ominus(T)}R\left(\cfrac{T_2-T_1}{T_1T_2}\right)$。

第7章化学反应速率

提纲

反应速率的表达形式，反应级数
一级反应的浓度随时间变化关系，半衰期
Arrhenius公式和活化能
过渡态理论
催化反应，用过渡态理论理解催化反应

1. 化学反应速率

对于反应$\ce{aA + bB -> cC + dD}$，反应物A在某一时刻$t$的瞬时反应速率定义为：$v_A=\lim\limits_{\Delta t\to 0}\cfrac{-\Delta(\ce{A})}{\Delta t}=-\cfrac{\mathrm d(\ce{A})}{\mathrm dt}$。

2. 反应级数

对于基元反应$\ce{aA + bB -> cC}$，微分反应速率方程可写为$v=k(\ce{A})^a(\ce{B})^b$，其中，$a$称为A的反应级数，$b$称为B的反应级数，总反应级数为$a+b$。
基元反应的反应速率与反应物的浓度的幂的乘积成正比。以基元反应$\ce{aA + bB -> cC}$为例，反应速率与反应物浓度的关系为：$v=k(\ce{A})^a(\ce{B})^b$。若$\ce{aA + bB -> cC}$是非基元反应，则：$v=k(\ce{A})^m(\ce{B})^n$，其中，$m$和$n$由实验确定。
对于一级反应$\ce{A -> P}$，微分反应速率方程为$-\cfrac{\mathrm d(\ce{A})}{\mathrm dt}=k(\ce{A})$，积分可得一级反应的积分反应速率方程：$\ln(\ce{A})-\ln(\ce{A})_0=-kt$。
半衰期是指反应进行一半所需的时间，一级基元反应的半衰期公式为：$t_{1/2}\approx\cfrac{0.693}k$。

3. 温度与反应速率·活化能

Arrhenius经验公式：$k=A\mathrm e^{-E_a/RT}$，其中，$k$为反应速率常数，$E_a$为实验活化能。
关于活化能的解释：碰撞理论、过渡态理论。

第8章酸碱平衡

提纲

酸碱电离常数表达式及其典型应用：一元弱酸弱碱pH、多元酸pH、中和反应体系pH、两性物质pH
重要应用：同离子效应、缓冲溶液、多元酸根类型随pH变化

1. 酸碱质子理论（Brønsted-Lowry酸碱理论）

在反应中，凡是能给出质子的分子或离子都是质子给体，称为酸；凡是能接受质子的分子或离子都是质子受体，称为碱。

2. 水的自耦电离平衡——溶剂间的质子传递

在水中，存在水的自耦电离平衡：$\ce{H2O + H2O <=> H3O+ + OH-}$，常温下其平衡常数为$K_w=1.0\times10^{-14}$，称为水的离子积。

3. 弱酸弱碱电离平衡——溶剂和溶质间的质子传递

一元弱酸、弱碱的电离平衡：
- 对于一元弱酸的电离反应$\ce{HA + H2O <=> H3O+ + A-}$，若溶液中HA的初始浓度为$c$（单位：$\pu{mol\cdot dm-3}$），电离度为$\alpha$，平衡常数为$K_a$，则有$K_a=\cfrac{[\ce{H3O+}][\ce{A-}]}{[\ce{HA}]}=\cfrac{[\ce{H3O+}]^2}{c-[\ce{H3O+}]}$，$K_a=\cfrac{c\alpha^2}{1-\alpha}$。
- 当$c/K_a\ge400$时，上两式可近似为$[\ce{H3O+}]=\sqrt{K_ac}$，$\alpha=\sqrt{\cfrac{K_a}c}$。
- $\mathrm{pH}=\mathrm pK_a+\lg\cfrac{[\ce{A-}]}{[\ce{HA}]}$。
- 按照酸碱质子理论，所谓的水解反应也是酸碱电离平衡，如$\ce{NH4+ + H2O <=> NH3 + H3O+}$，$K=\cfrac{K_w}{K_b(\ce{NH3.H2O})}$。
多元弱酸、弱碱的电离平衡：通常二元弱酸的电离常数$K_{a_1}\gg K_{a_2}$，所以在计算多元弱酸的$[\ce{H3O+}]$时，可以忽略第二步及其后的电离。
两性物质的酸碱性：$K_a$和$K_b$大者占优，$[\ce{H3O+}]=\sqrt{K_aK_b}$。

4. 酸碱电离平衡的移动

在弱电解质溶液中加入同一种离子的强电解质时，平衡会向反向移动，从而降低弱电解质的电离度，称为同离子效应。
酸碱指示剂是一类有机弱酸碱，弱酸的通式写为HIn。

5. 缓冲溶液

由弱酸或弱碱的共轭酸碱对（HA和$\ce{A-}$组成的混合溶液能缓解外加少量酸、碱或水的影响，从而可以保持溶液的pH不发生显著变化，这种溶液称为缓冲溶液。
配置缓冲溶液要考虑的因素为：
- 要选用$\mathrm pK_a$等于或接近目标pH的共轭酸碱对；
- 弱酸及其共轭碱的最佳浓度比为1:1；
- 适当提高缓冲溶液的浓度。

第9章沉淀溶解平衡

提纲

溶度积，溶度积与溶解度的关系，判断沉淀是否生成
沉淀的溶解和转化，同时存在沉淀溶解平衡与酸碱平衡的计算

1. 溶度积

难溶电解质在水溶液中具有如下的电离平衡：$\ce{A_mB_n(s) <=> mA^{n+}(aq) + nB^{m-}(aq)}$，$K^\ominus=\ce{[A^{n+}]^m.[B^{m-}]^n}$，平衡常数$K^\ominus$称为溶度积，常写为$K_{\mathrm{sp}}$。

2. 沉淀的生成、溶解、转化

盐效应：强电解质会使沉淀溶解度增大；其他的副反应：如配合作用$\ce{AgCl + Cl- -> AgCl2-}$。
所用酸越强，难溶物$K_{\mathrm{sp}}$越小，生成的酸越弱，越有利于沉淀溶解。
沉淀倾向于转化为$K_{\mathrm{sp}}$更小的沉淀。
分步沉淀：当多种离子混合在一起时，控制条件使各种离子逐一沉淀。

第10章氧化还原·电化学

提纲

氧化还原方程式的配平
电极电势的概念
$E$－$\Delta G$－$K$之间的关联
Nernst方程及其应用，利用电极电势计算酸碱和沉淀平衡
典型化学电源的电极反应及相关计算
电解池及其应用、超电势

1. 原电池

原电池由电极、电解质溶液、盐桥和导线组成。
- 电极：固体、液体或气体。
- 电解质：水溶液、有机溶液、凝胶、熔盐、固体。
- 两电极可以置于同一电解质中，也可以置于两种不同的电解质中，两种电解质通过盐桥或膜隔离。
表示形式：(-) 负极 | 电解质 | 正极 (+)。
- 气体写出压力和相应的固体催化剂；溶液写出浓度；如有两种电解质，用||分隔，代表盐桥或膜。
对于铜锌电池：
- 总反应：$\ce{Zn + Cu^{2+} -> Zn^{2+} +Cu}$。
- 负极反应：$\ce{Zn <=> Zn^{2+} + 2e}$。
- 正极反应：$\ce{Cu^{2+} +2e <=> Cu}$。
- 电池符号：$(-) \ce{Zn \mid Zn^{2+} \| Cu^{2+} \mid Cu} (+)$。
电动势的来源：两电极得失电子能力不同。
电解质的作用：构成回路，消除电极电荷积聚。

2. 化学电源

化学电源（电池）：利用自发的化学反应产生电能的装置。一次电池：仅可使用一次；二次电池：可多次充放电反复使用。
能量密度：电池的核心指标，$W = Q \cdot E$，其中，$W$是能量密度，即单位质量（体积）存储的电能，$Q$是电池容量，单位质量（体积）存储的电量，$E$是电池的工作电压。

3. 电极电势和氧化还原平衡

电场中某一点的静电势能：将单位正电荷从无限远移至该位置所需做的功。
电势越高，体系做功越多，电极越易得电子，氧化性越强。
标准氢电极的电极电势被设为零，即$\varphi^\ominus _{(\ce{H+/H2})} = 0$。
水溶液中各氧化还原电对的标准电极电势可以用来表达相应电对的氧化还原能力，电极电势越正，表示该物质氧化态的氧化性越强。
在电池反应中，若电子转移数为$n$，则转移的电量为$nF$，$F$为1 mol电子的电量。电池反应所做的电功为$-W'_{max} = nFE ^\ominus _池 = -\Delta G ^\ominus _{(T)}$。
由于$\Delta G ^\ominus _{(T)} = -RT\ln K ^\ominus$，所以$E ^\ominus _池 = \cfrac{RT}{nF} \ln K ^\ominus$，当$T = \pu{298.15 K}$时，$E ^\ominus _池 = \cfrac{\pu{0.0592 V}}n \lg K ^\ominus$。
对于氧化还原反应，氧化还原电对的电极电势差越正，反应趋势越大。一般$E = \pu{0.2 \text{~} 0.4 V}$可以认为能够反应完全。

4. 电极电势的间接计算

电极电势是强度量，不具有加和性，必须和电量相乘后才能进行加和。
$n _1 FE ^\ominus _1 = n _2 FE ^\ominus _2 + n _3 FE ^\ominus _3$。

5. 浓度对电极电势的影响——Nernst方程式

电池反应$\ce{a ox1 + b red2 <=> c red1 + d ox2}$的Nernst方程式为：$E _池 = E ^\ominus _池 - \cfrac {\pu{0.0592 V}}n \lg \cfrac{\ce{(red1)^c(ox2)^d}}{\ce{(ox1)^a(red2)^b}}$。
有$\ce{H+}$参与的反应，pH对$\varphi$有显著影响，一般酸性越强，氧化性越强。

6. 由电极测定求$K_{\mathrm{sp}}$或pH

以对$\ce{H+}$敏感的玻璃电极与饱和甘汞电极组合为例，总电池电动势为$E _池 = E _{饱和甘汞} - E _玻 = ($常数$+ \pu{0.0592 pH) V}$。

7. 分解电势和超电势

电解池的理论分解电压等于电池电动势，但是实际分解电压总是高于理论值，这是由于电解池存在超电势（$\eta$）。

第11章原子结构

提纲

现代原子结构模型描述
量子力学基本思想：能量量子化、波粒二相性、测不准原理
Bohr原子模型及其对氢原子光谱的解释
Schrödinger方程，类氢原子轨道特点
多电子原子核外电子排布的规律
元素周期表及元素主要性质的变化规律

1. 经典核原子模型的建立

1897年，Thomson阴极射线实验，测定了电子的荷质比。
1909年，Millikan油滴实验，测定了电子的电荷。
1911年，Rutherford $\alpha$粒子散射实验，建立了原子的经典核型结构：原子是空旷的，主要质量和正电荷集中于原子核上。

2. 氢原子光谱和Bohr氢原子理论

模型的提出基于下述重要的实验现象及对实验的解释：
- 黑体辐射：Planck能量量子化假说：电磁辐射的能量不连续，而是一个最小能量的整数倍，即$E = nh \nu$；
- 光电效应：Einstein光子假说：引入光子概念，成功解释了光电效应。光子能量$E = h\nu = E_0 + E_k$。光子有能量、无质量，即Planck的“能量量子”；
- 氢原子线状光谱：Rydberg经验式$\cfrac 1 \lambda = R_H \left(\cfrac 1 {n^2_1} - \cfrac 1 {n^2_2}\right)$。
黑体：能吸收全部外来电磁辐射的物体。黑体辐射光谱只与温度有关。
氢原子结构模型的三个假设
- 定态假设：核外电子只能在具有确定半径和能量的特定轨道上围绕原子核运动，电子在这些轨道上运动时并不辐射出能量，$r = \cfrac {Ze^2} {4\pi \varepsilon_0 mv^2}$。
- 角动量量子化假设：核外电子在上述轨道上运动时，角动量（$L$）是量子化的：$L = n \cfrac h {2\pi}$，其中，$n$称为量子数，$h$为Planck常数。圆形轨道运动的电子角动量为$L = mvr$，从而可求得电子绕核运动的轨道半径$r = \cfrac {\varepsilon_0 n^2 h^2} {\pi m Z e^2}$，$E = - \cfrac {m e^4} {8 \varepsilon_0^2 h^2} \cfrac {Z^2} {n^2}$。代入相关常数可得电子运动的轨道半径：$r = 52.93 \cfrac {n^2} Z (\pu{pm})$，以及电子在轨道上运动的能量$E = - B \cfrac {Z^2} {n^2}$，$B = - \pu {13.6 eV}/$电子。
- 光子的吸收与辐射：电子在不同轨道之间跃迁时，原子会吸收或辐射出光子，其能量为：$\Delta E = \mid E_2 - E_1 \mid = h\nu = \frac {hc} \lambda$。

3. 微观粒子特性及其运动规律

波粒二象性：
- de Broglie提出实物粒子的波粒二象性，即$\lambda = \cfrac h P = \cfrac h {mv}$。
- 实验验证：晶体对电子束的衍射。
不确定性关系：
- Heisenberg测不准原理：$\Delta x \cdot \Delta P \ge \cfrac h {4\pi}$，是微观粒子的固有特性，并非测量技术造成。

4. 氢原子的量子力学模型

波函数：
- Schrödinger提出了波动力学方程式，该方程式的合理解只限于若干分立的能量值，这也就是量子化。
- Schrödinger方程的解是表述电子在原子轨道上运动的波函数$\Psi$，又称为原子轨道。
物理意义：
- $\Psi(r, \theta, \varphi)$：波函数，取值为复数，描述电子运动行为，也称为原子轨道。
- $\Psi ^ 2 = \Psi \Psi ^ *$：某位置电子出现的概率密度。
- $4 \pi r ^ 2 R ^ 2$：距离原子核$r$处出现电子的概率。
量子数：一个原子轨道由三个量子数决定，分别是主量子数$n$、角量子数$l$、磁量子数$m$。
- $n$（电子层数）：电子离核的距离，决定电子能量。
- $l$（电子亚层）：电子空间角度分布，决定电子角动量。
- $m$：轨道的空间取向，电子角动量在磁场方向的分量。
- 一个电子的状态有四个量子数决定，除以上三个量子数之外，还有自旋量子数$m_s$：电子具有磁矩，在磁场中有两个分量。
- 各个量子数的取值范围：$n$为正整数，$l$为0到$n-1$之间的数，$m$为$-l$到$+l$之间的整数，$m_s$为$+\frac12$或$-\frac12$。
氢原子波函数和电子云图像
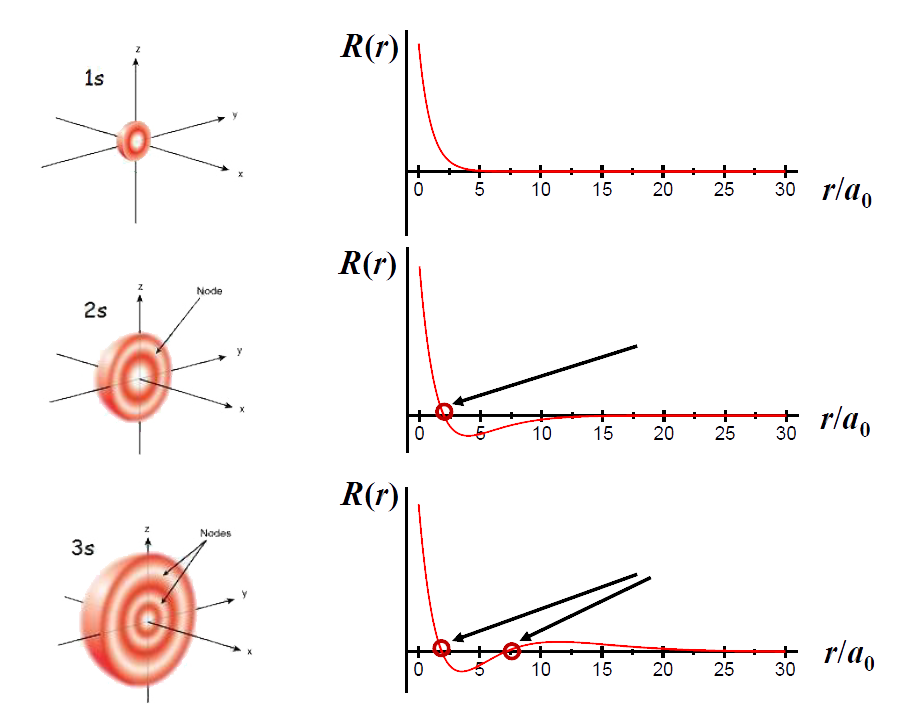
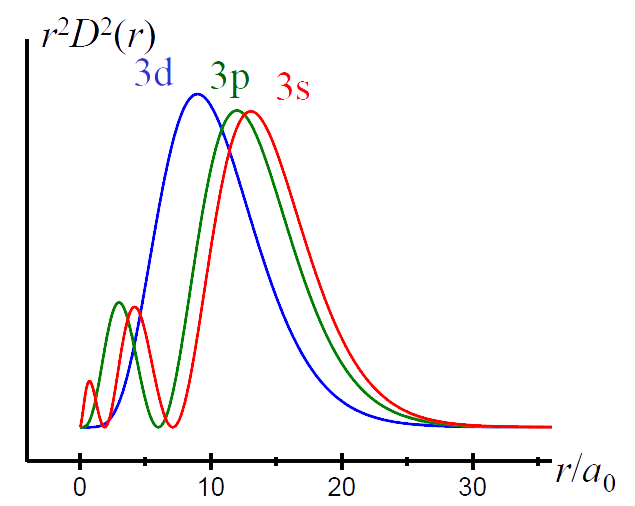
- 径向分布：反映了电子距核的距离，电子能量的主要决定因素。电子云径向密度分布$R^2(r)$；电子云径向分布$r^2 R^2(r)$或$D(r)$；波函数径向分布$R(r)$。
- 角度分布：反映了电子云的形状及电子波函数的叠加性，对化学键的形成具有重要意义。电子云角度分布$Y^2(\theta, \varphi)$；波函数角度分布$Y(\theta, \varphi)$。
- 电子云空间分布$\Psi(r, \theta, \varphi)$
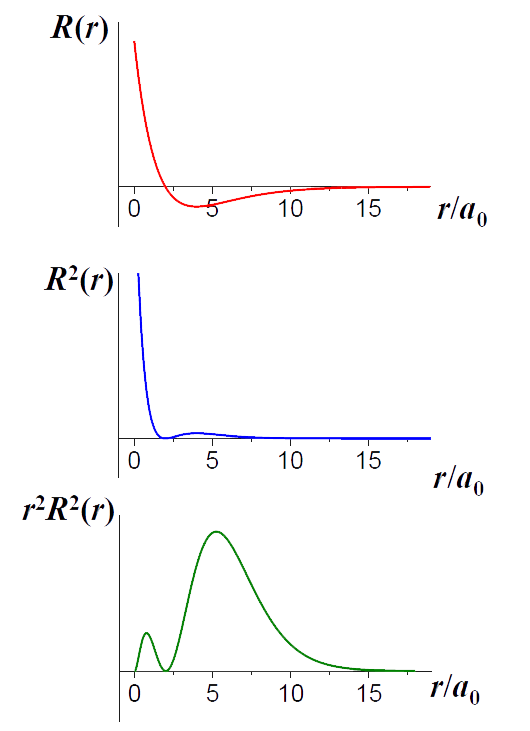
区别$R$、$R^2$、$r^2R^2$
- $R(r)$：波函数，可正可负。
- $R^2(r)$：概率密度，正值，$r = 0$时最大。
- $r^2R^2(r)$：概率径向分布函数，正值，极大值不出现在$r = 0$。
原子轨道的空间分布：径向节面数：$n - l - 1$；角度节面数：$l$。

s轨道。自上而下：$R^2(r)$、$\Psi^2(r, \theta, \varphi)$、$Y^2(\theta, \varphi)$

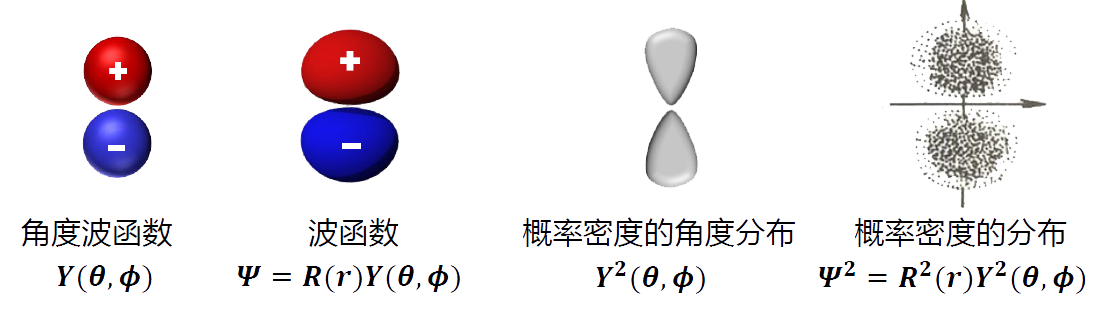
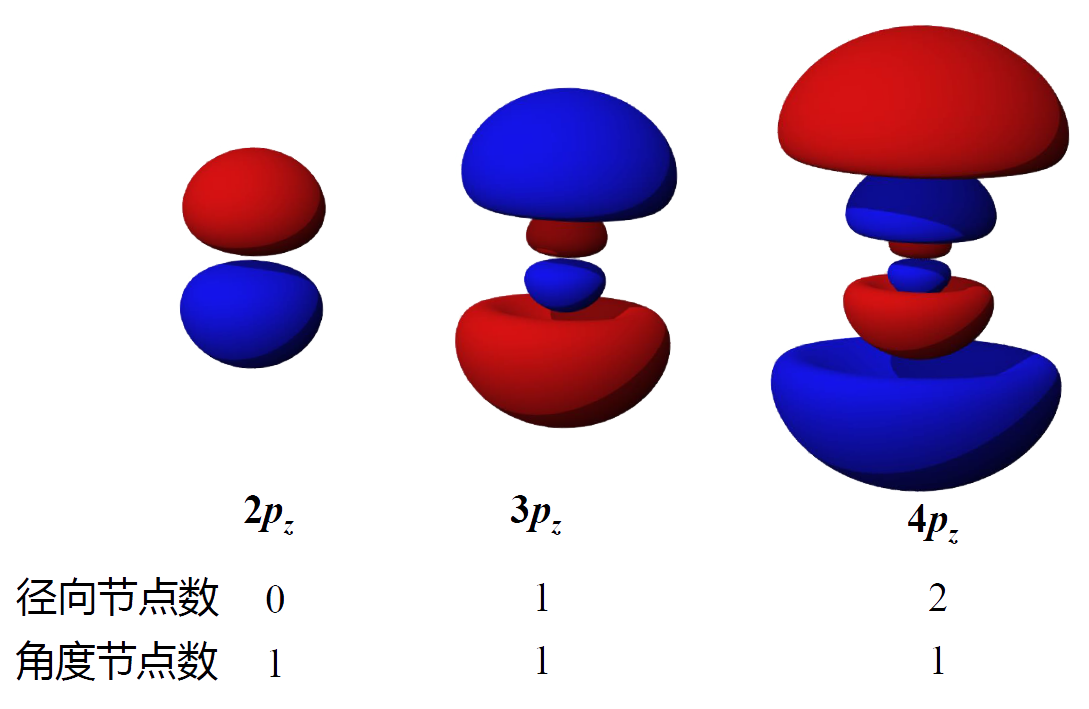
5. 多电子原子结构与周期律

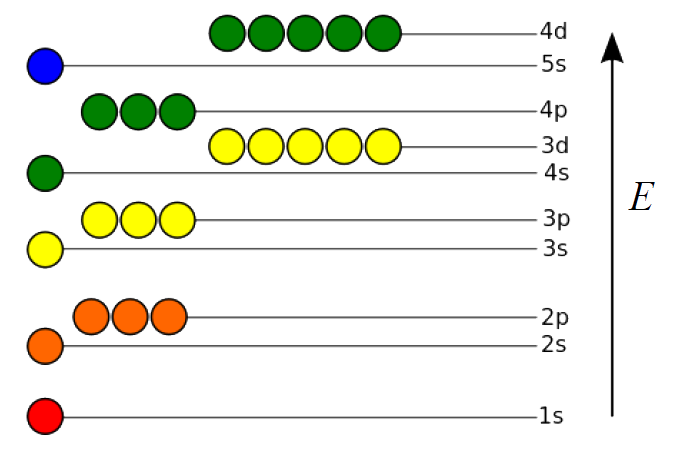
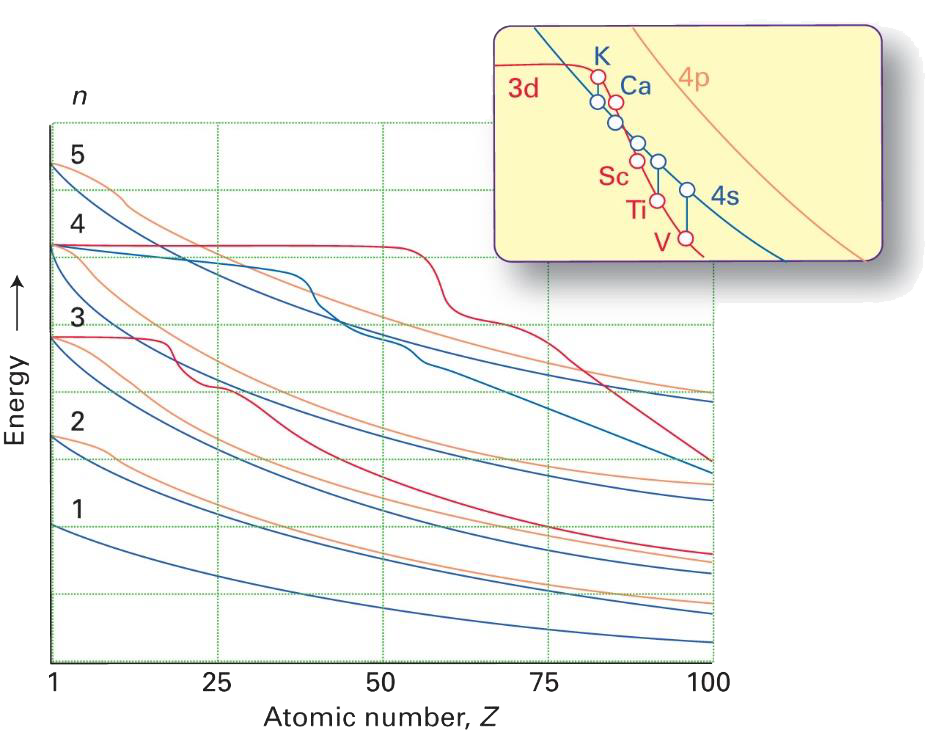
多电子原子的轨道能级：$n$和$l$都不同的轨道能量会发生交错，轨道能量和核电荷数和电子填充情况都有关，使整体能量最低。
- 在类氢原子中，颜色相同的轨道能量简并。由于屏蔽和钻穿效应，多电子原子中能级不再简并。
- 不同主量子数原子轨道的能级关系为$E_{1\mathrm s} < E_{2\mathrm s} < E_{3\mathrm s} < E_{4\mathrm s}$。
- 相同主量子数、不同角量子数的多电子原子轨道的能量关系为$E_{n\mathrm s} < E_{n\mathrm p} < E_{n\mathrm d} < E_{n\mathrm f}$。
- 由于能级分裂，不同主量子数的原子轨道还会发生能级交错，即$E_{6\mathrm s} < E_{4\mathrm f} < E_{5\mathrm d} < E_{6\mathrm p}$。
屏蔽效应：其他电子的排斥作用削弱了核的正电荷。
- 外层电子：感受到的屏蔽作用强，能量升高较多。
- 内层电子：感受到的屏蔽作用弱，能量升高较少。
钻穿效应：$n$相同，$l$不同的轨道，电子云径向分布不同，电子云穿透内层而钻穿到原子核附近以回避其他电子屏蔽的作用，使能量降低。钻穿能力： $n\mathrm s > n\mathrm p > n\mathrm d > n\mathrm f$。
核外电子排布的基本原则：
- Pauli不相容原理：在同一个原子中没有两个4个量子数完全相同的电子；同一原子轨道仅可容纳自旋相反的两个电子。
- 能量最低原理：核外电子在各个原子轨道的排布方式应使整个原子处于最低的能态。
- Hund原则：电子在能量相同的轨道上分布时，总是尽可能以自旋相同的方向分占不同的轨道。

6. 元素基本性质的周期性变化规律

原子半径：
- 同一主族由上到下原子半径一般增大。
- 同一短周期由左到右原子半径减小。
- 过渡元素从左到右半径呈减小的趋势，减小幅度比主族元素小。
电离能：
- 基态的气体原子失去最外层第一个电子所需的能量称为第一电离能（$I_1$）。
- 同一主族由上到下电离能减小。
- 同一周期由左到右电离能一般增大，增大幅度随周期数增大而减小。
- 一般来说具有半充满、全充满价电子构型的元素都有比较大的电离能。
电子亲和能：
- 一个气态原子得到一个电子所放出的能量称为电子亲和能（$E_{ea}$），通常第一电子亲和能为正值。
- 电子亲和能的周期变化规律与电离能相似，但一般第二周期元素的电子亲和能小于第三周期元素。这是由于第二周期非金属元素原子半径较小，电子之间排斥力较强，电子亲和能较小。
电负性：
- Pauling将电负性（$\chi$）定义为分子中原子对成键电子吸引能力的量度，公式：$\chi_\ce{A} - \chi_\ce{B} = 0.089 \sqrt\Delta$，其中，$\Delta = \mathrm{EB _{(\ce{A-B})} - \sqrt{EB _{(\ce{A-A})} EB _{(\ce{B-B})}}}$，单位：$\pu{kJ * mol-1}$。
- Mulliken电负性公式：$\chi = \frac 1 2 (I + E)$，（单位：eV）。
- 同族元素由上到下电负性减小。
- 同一周期由左到右电负性增大。

第12章化学键与分子结构

提纲

微观成键作用的分类和键的强度范围
离子键：晶格能的概念和计算，离子半径
共价键理论：Lewis结构式，价键理论基本思想，杂化轨道理论，分子构型和极性判断，共振论，分子轨道理论基本思想，同核双原子分子的分子轨道，离域键，简单分子的分子轨道
金属键理论：定义和描述，能带概念，导电性的解释
分子间作用力和氢键：定义和类别，作用力强弱，物理化学性质判断

1. 离子键理论

离子键的本质是正负离子之间的静电吸引力，主要特点是既没有方向性也没有饱和性。
离子化合物熔融状态下或水溶液中都具有导电性。
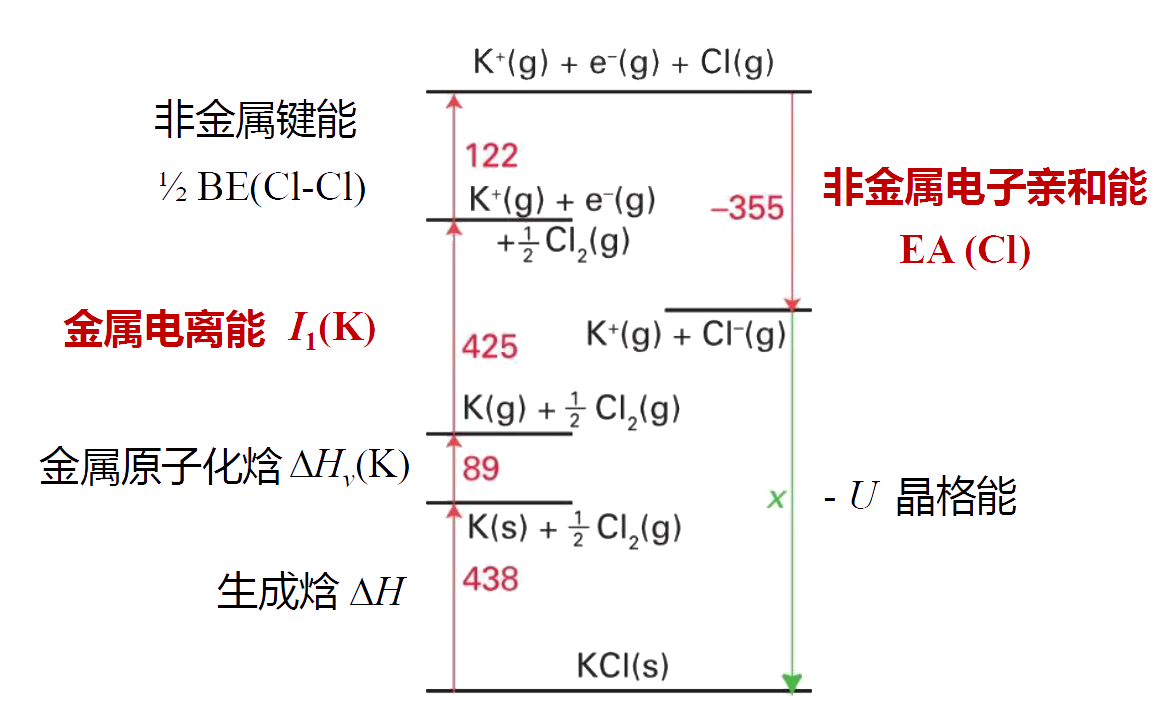
晶格能（$U$）：气态正离子与负离子结合形成1 mol离子晶体时所释放出来的能量。$\ce{m M^{x+} (g) + x X^{m-} (g) -> M_mX_x (s)}$，$\Delta H = - U$。离子键的强度通过晶格能给出。
- 利用Born-Haber循环可以从其他热力学数据计算晶体的晶格能。
- 对于特定结构类型的离子晶体，离子电荷越高、离子半径越小，晶格能越大。
在晶体中通过正负离子间的距离来计算离子半径，同一离子在不同化合物中的半径不一定完全相同。

2. 经典Lewis学说

Lewis结构核心是8电子规则，又称八隅律。
书写规律：
- 确定原子之间连接方式，用短线连接，表明一对电子。
- 分配剩余电子，每个原子都需要满足八隅律。
- 书写孤对电子，标上形式电荷。Lewis结构式必须表明孤对电子。
- 检查结构的合理性。
形式电荷不等于分子中原子实际的电荷状态。
- 各原子形式电荷最小的结构（一般在+1和-1之间）通常能量最低。同号电荷的原子不能相邻接。
- 一般情况下，形式负电荷归属于电负性较大的元素，形式正电荷归属于电负性较小的元素。
八隅体规则能够比较好地解释某些主族元素化合物的成键情况。
八隅体规则的局限性在于：
- 不能说明共价键的本质。
- 无法解释$\ce{PCl5}$等分子的形成。
- 不能解释某些分子体系的现象，如$\ce{O2}$的顺磁性。

3. 价键理论

价键理论的核心是原子之间由于静电吸引而相互靠近，具有未成对电子的原子轨道发生重叠，原子通过公用自旋相反的电子使能量降低而成键。
价键理论对于共价键本质的认识是：共价键本质也是静电作用，是电子对占据原子轨道重叠而形成的新轨道。
共价键的特点是具有方向性和饱和性。
为解释原子数目及其形成分子的结构，Pauling提出了杂化轨道的概念：同一原子中能量相近的不同类型轨道可以相互叠加，组成相同数目的、能量完全相同的杂化原子轨道。
价键理论认为化学键中电子是定域的，Pauling引入了共振的概念，即某些分子的结构是两种或两种以上结构的共振体。

4. 分子轨道理论

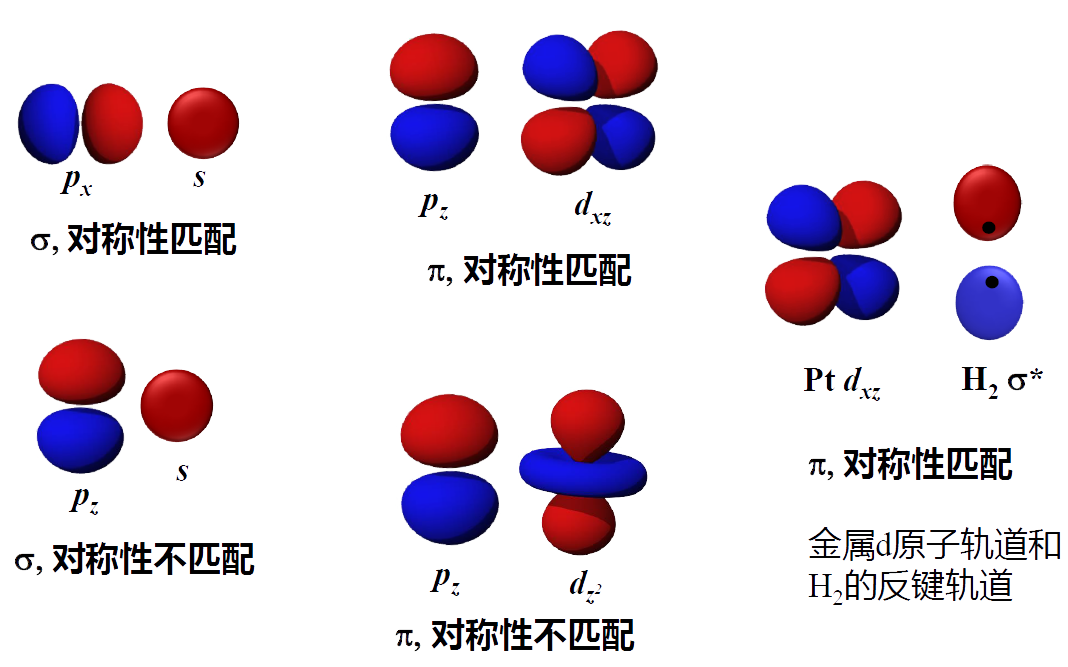
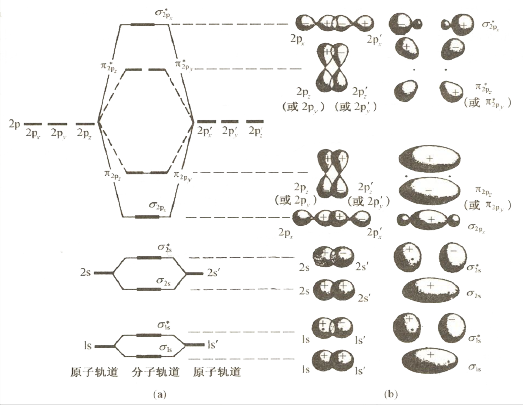
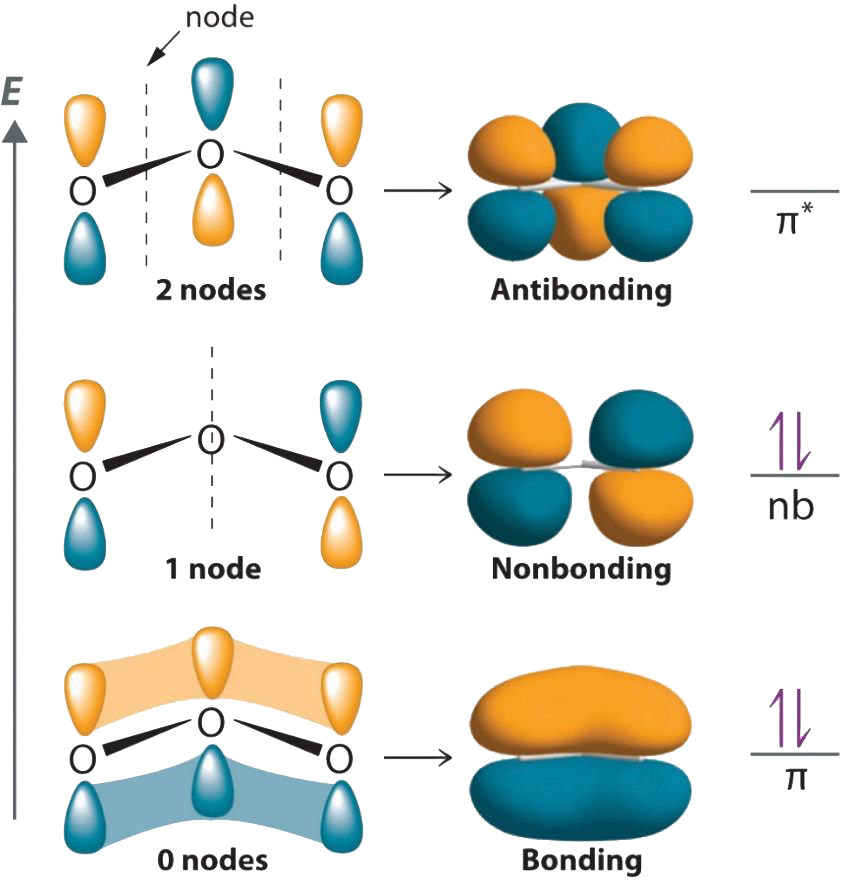
分子轨道可由原子轨道线性组合而成，原子轨道组成分子轨道时，轨道数不变：$\Psi = \Psi_1 \pm \Psi_2$。
分子轨道的能量可以低于、等于或高于原子轨道，分别称为成键、非键和反键轨道。原子轨道组成分子成键轨道时，必须满足对称性匹配原则、能量近似原则和最大重叠原则。
- 对称性匹配：$\sigma$键关于键轴对称；$\pi$键关于节面反对称。例如s、$\mathrm d_{z^2}$轨道不能成$\pi$键。
- 能量相近：同核双原子分子中，1s和2s难以发生有效重叠。
- 最大重叠：多原子分子中距离很远的两个原子其轨道重叠作用较弱。
- 运用轨道有效组合的原则，特别是对称性原理，排除不可能相互组合的原子轨道，简化分子轨道的计算。
电子在分子轨道上的排布遵循能量最低原理、Pauli不相容原理和Hund规则。
电子在分子轨道排布后，键级=（成键轨道中的电子数$-$反键轨道中的电子数）$/2$。
轨道数不变：$n$个AO线性组合后得到$n$个MO。
轨道能量守恒：MO能量总和等于AO能量总和。
成键轨道：能量低于AO，来自$\Psi_{\mathrm{AO}}$之间的增强叠加；电子填入成键轨道使能量降低。
反键轨道：能量高于AO，来自$\Psi_{\mathrm{AO}}$之间的减弱叠加；电子填入反键轨道使能量升高。
非键轨道：没有参与MO的AO，电子填入非键轨道能量不变。
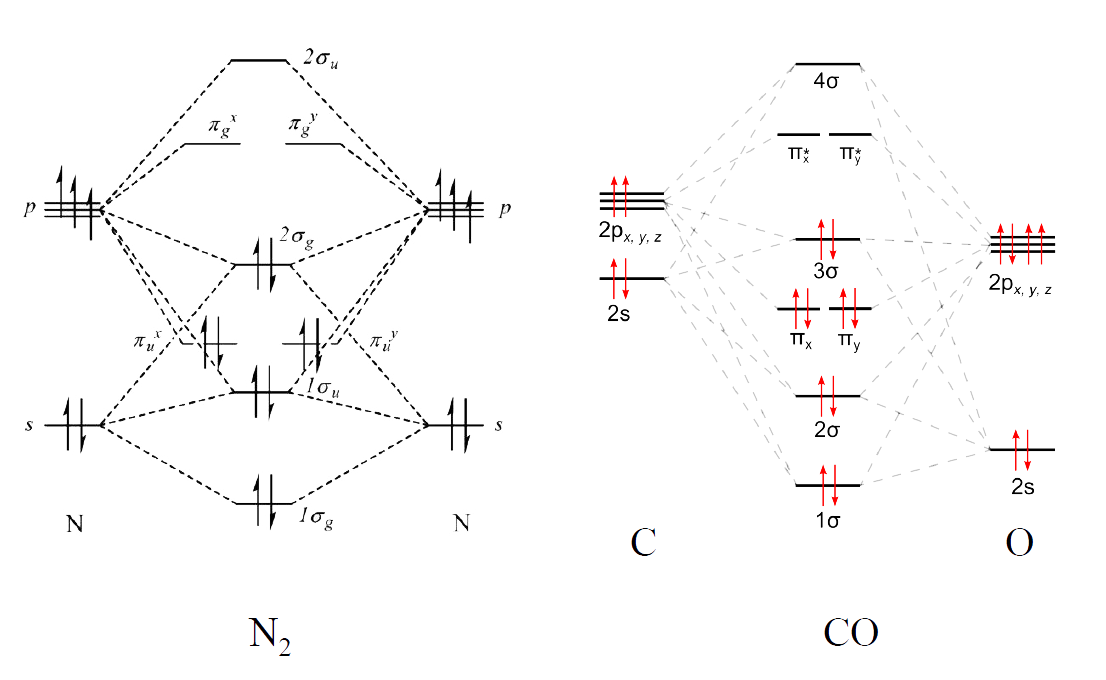
第二周期同核双原子分子的分子轨道：MO理论可完满解释$\ce{O2}$的顺磁性。
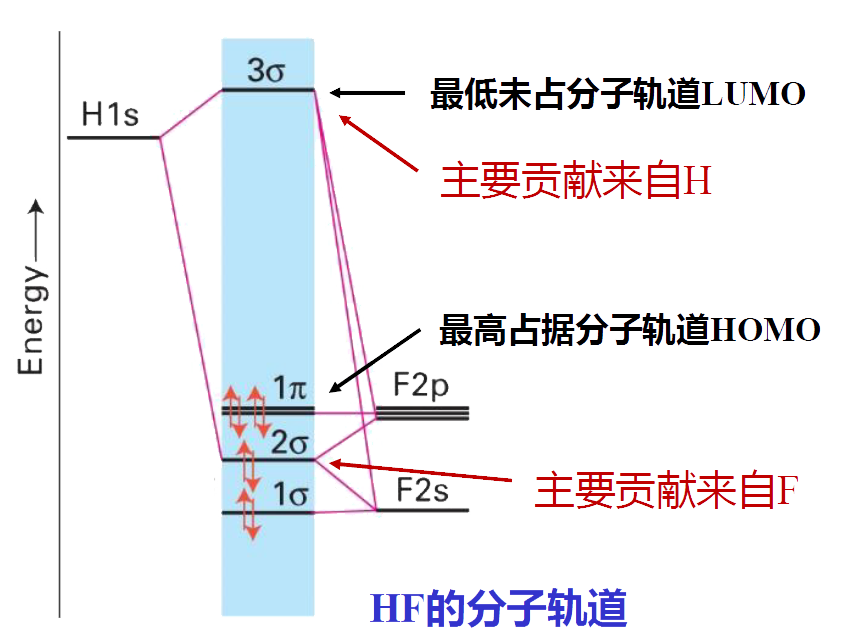
异核双原子分子的分子轨道：F轨道能量更低，成键轨道中F的成分更大，相当于H向F转移了部分电子。
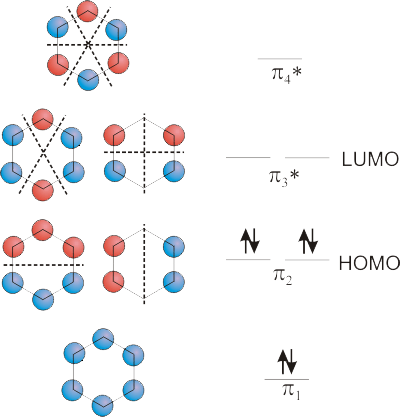
离域$\pi$键：
- 苯：6个p轨道构成6个分子轨道，6个电子填充其中3个成键轨道。
- 臭氧：3个p轨道构成3个分子轨道，4个电子填充成键和非键轨道。
对比：
- VB易与原子轨道和分子几何形状关联，无法解释非经典成键。
- MO能解释非传统化学键（奇数电子键、缺电子键、离域键），不容易看出原子之间的键合关系。
- 用VB处理经典的成键，用MO处理非经典的成键。

5. 价层电子对互斥（VSEPR）理论

VSEPR理论认为，分子中的价层电子对之间因为静电排斥趋向于尽可能远离。
核心：合理计算中心原子的键对和孤对。
要点：中心原子与端基成键时端基满足8电子。
判断方式：
- 计算键对和孤对的数目：键对包括单键、双键、叁键，后两者均按一个键对处理。对任一分子$\ce{AX_m}$，中心原子为A，A与X成键的键对数$\mathrm{BP} = m$，孤对$\mathrm{LP} = n =$（中心原子价电子 $-$ 周围原子满足8电子所需电子）$/2$。
- 计算价电子总数：价电子总数$= m + n$。
- 价电子对在中心原子周围分布时尽可能远离，即采取尽可能对称的分布。
- 分子构型判断：不含孤对电子时，分子构型与价层电子对分布相同；当存在孤对电子时，分子的形状与孤对电子无关。
价层电子对相互排斥作用：$\mathrm{LP-LP > LP-BP > BP-BP}$，$90^\circ \gg 120^\circ \gg 180^\circ$。
等电子原理：当分子、离子或某一基团含有相同的非氢原子个数且价电子总数相同时，则其非氢原子构型往往相同。

6. 分子的极性

分子的极性由键的极性及分子的结构决定。当分子中正负电荷不重合时，分子为极性分子。
分子的极性可用偶极矩表示为$\mu = qd$.

7. 金属键理论

金属的特征：金属光泽、良导电性、良导热性、延展性。
自由电子模型：在金属中，价电子处于自由运动状态，而正离子浸泡在自由电子形成的海洋中。
能带理论：基于分子轨道理论，从金属原子轨道的组合形成能带的角度分析金属的成键，对金属电子结构的描述更加准确。

8. 分子间作用力和氢键

分子间作用力又称van der Waals力，是一种比化学键弱得多的相互作用，分为三种：
- 取向力：分子固有偶极之间的静电相互作用。
- 诱导力：分子固有偶极与诱导偶极之间的相互作用。
- 色散力：瞬时诱导偶极之间的相互作用。
极性分子与非极性分子之间同时存在以上三种力，极性分子与非极性分子之间存在诱导力和色散力，非极性分子之间只有色散力。
对于变形性较大而极性弱的分子而言，色散力通常是分子间作用力中最重要的部分。
分子间作用力对于物质的物理性质有较大影响。
共价半径和vdW半径：
- 共价半径：同核双原子分子中两个原子核间距的一半。
- van der Waals半径：相邻两个分子中相互接触的两个原子核间距的一半。
氢键是一种氢给体（XH）与氢受体（Y）之间通过氢原子的相互作用：$\ce{X - H \bond{...} Y}$。其中，X和Y具有电负性高、半径小的特点，通常为N、O、F原子。
氢键的强度介于van der Walls力和化学键之间，约为10 ~ 40 kJ/mol，可以存在分子间或分子内。X、Y电负性越高，氢键键能越大。
强氢键类似共价键，有一定的饱和性和方向性。
弱氢键主要是静电相互作用，无饱和性和方向性。
氢键对于物质的熔点、沸点以及溶解度有很大影响。

第13章晶体与晶体结构

提纲

晶体学基本定义：点阵、晶格单位、晶胞
七大晶系和14种Bravis点阵形式
等径圆球最密堆积及其中的四面体和八面体空隙
典型晶体结构及其描述方法
成键和晶体类型的过渡
非晶体

1. 晶体的特征

晶体通常具有自发形成的规则的几何外形；
晶体具有固定的熔点，而非晶体没有固定熔点；
晶体呈现各向异性。

2. 晶体结构的周期性

晶体内部的结构单元（原子、分子、原子团或离子）在空间作有规则的周期性排列。周期性是晶体的显著特征。
晶体结构的两大要素：重复的单元和周期性重复的方式。
晶胞$=$晶格单位$+$结构单元。
晶胞：晶格单元中的点阵点替换为结构单元；晶格单位：点阵中的平行六面体格子；结构单元：重复的是什么。
晶体具有平移周期性，三维晶体的晶格单位和晶胞必须是平行六面体。
点阵：将结构单元抽象成一个点，这些点在空间排列的方式。用来描述结构单元以什么方式重复。
晶胞参数：3个边长$a$、$b$、$c$；3个夹角$\alpha (b\wedge c)$、$\beta (a\wedge c)$、$\gamma (a\wedge b)$。
根据晶体的对称性划分为7大晶系，14种空间点阵式。
Bragg方程：$2d\sin \theta = n\lambda$。其中，$d$为晶面间距，$\lambda$为入射X射线波长，$\theta$为衍射角，$n$为衍射级数。

7种晶系参数表
晶系	晶胞参数	对称性要求	晶体实例
立方	$a = b = c, \alpha = \beta = \gamma = 90 ^ \circ$	4个三次对称轴	Cu
六方	$a = b \neq c, \alpha = \beta = 90 ^ \circ, \gamma = 120 ^ \circ$	1个六次对称轴	Mg
四方	$a = b \neq c, \alpha = \beta = \gamma = 90 ^ \circ$	1个四次对称轴	$\ce{\beta-Sn}$
三方	简单三方 $a = b \neq c, \alpha = \beta = 90 ^ \circ, \gamma = 120 ^ \circ$	1个三次对称轴	$\ce{\alpha-SiO2}$
三方	菱面体格子 $a = b = c, \alpha = \beta = \gamma \neq 90 ^ \circ$	1个三次对称轴	$\ce{\alpha-Al2O3}$
正交	$a \neq b \neq c, \alpha = \beta = \gamma = 90 ^ \circ$	3个两次对称轴或 1个两次对称轴+2个对称面	$\ce{HgCl2}$
单斜	$a \neq b \neq c, \alpha = \gamma = 90 ^ \circ$	1个两次对称轴或 1个对称面	$\ce{KClO3}$
三斜	$a \neq b \neq c, \alpha \neq \beta \neq \gamma \neq 90 ^ \circ$	无	$\ce{CuSO4.5H2O}$

7种晶系和14种布拉维晶格对应表参考资料：维基百科编者. 布拉维晶格 [G/OL]. 维基百科, (2019-04-25) [2019-11-03]. https://zh.wikipedia.org/w/index.php?title=%E5%B8%83%E6%8B%89%E8%8F%B2%E6%99%B6%E6%A0%BC&oldid=54166188.
晶系（7种）	布拉维晶格（14种）
晶系（7种）	简单（P）	体心（I）	底心（C）	面心（F）
立方	简单立方	体心立方		面心立方
六方	简单六方
四方	简单四方	体心四方
三方	R心六方
正交	简单正交	体心正交	底心正交	面心正交
单斜	简单单斜		底心单斜
三斜	简单三斜

3. 等径圆球的堆积

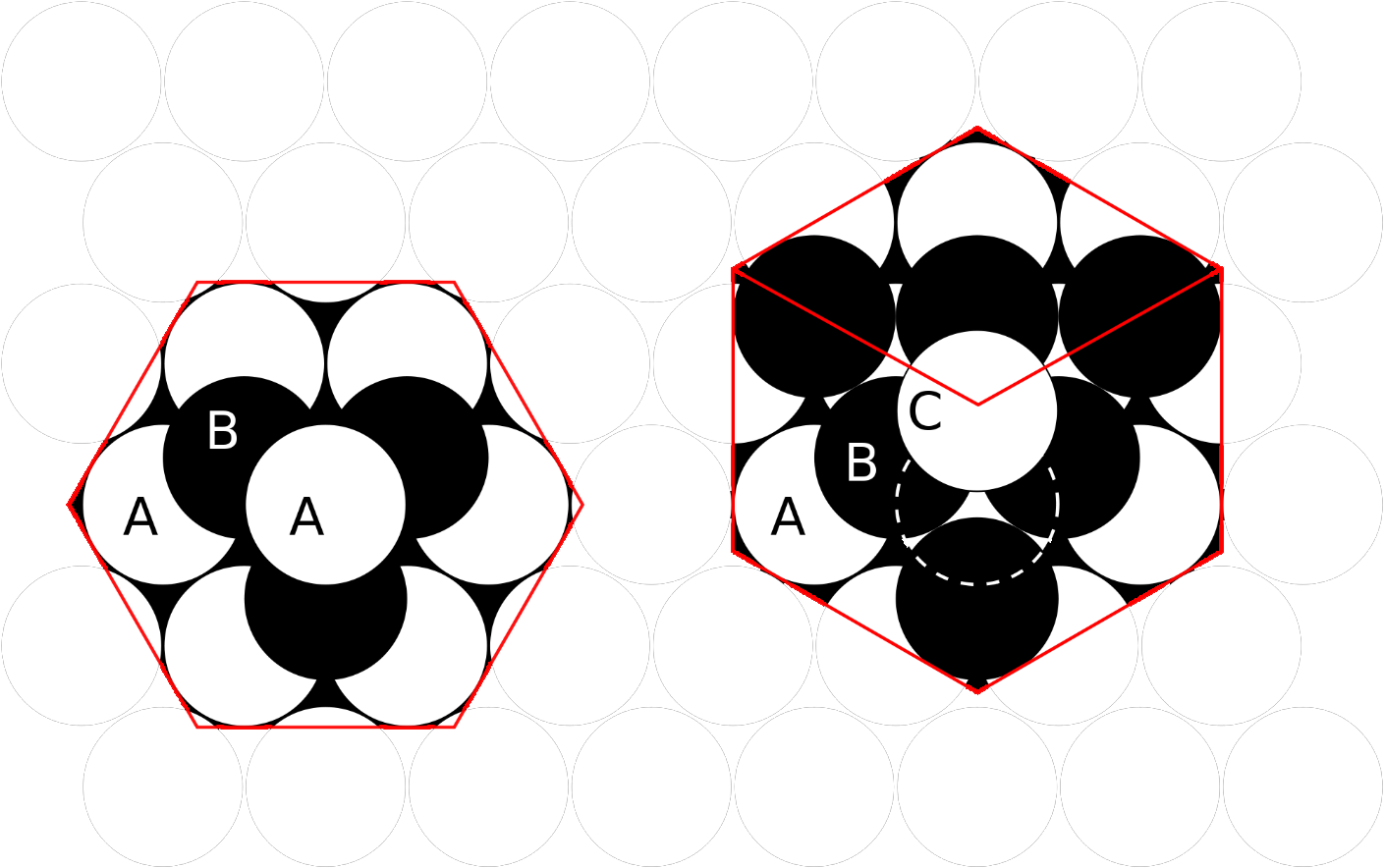
简单立方堆积：非密堆积，空间利用率52%；体心立方堆积：符号A2，非密堆积，空间利用率68%。
密置结构：空间占有率最高的排布方式，为74%。
等径圆球的两种密堆积形式：六方密堆积（hcp，A3）、立方密堆积（ccp，A1）。每个圆球的配位数均为12。
- ABC型的堆积等价于面心立方结构，密堆积方向垂直于$C_3$轴（即[111]矢量方向），晶胞的轴沿三个$C_4$轴方向。
由$N$个等径圆球组成的三维结构中，可形成$2N$个由4个球围成的“四面体空隙”、$N$个由6个球围成的“八面体空隙”。若圆球半径为$r$，则四面体空隙可容纳半径为$0.225r$的小球，八面体空隙可容纳半径为$0.414r$的小球。
- 八面体空隙：由6个球围成；每个球周围有2组（每组3个）共边的八面体空隙，共6个八面体空隙。
- 四面体空隙：由4个球围成；每个球周围有2组（每组4个）共顶点的四面体空隙，共8个四面体空隙。
- 立方密堆中，八面体空隙：体心和每条棱的中心；四面体空隙：$(x, x, x)$，$x = \frac 1 4$或$\frac 3 4$，共8个位置。
- 六方密堆中，八面体空隙：$(\frac 2 3, \frac 1 3, \frac 1 4)$，相当于密堆层中的C位；四面体空隙：$(0, 0, \frac 3 8)$，$(\frac 1 3, \frac 2 3, \frac 3 8)$，每个质点的正上下方$\frac 3 8$处。

4. 晶体的基本类型与结构

根据构成晶体的质点间作用力的类型分为四大基本类型：金属晶体，离子晶体，分子晶体，共价晶体。
金属晶体作用力：金属键；结构特征：等径圆球堆积，倾向于密堆积。
离子晶体作用力：离子键，无方向性和饱和性，故倾向于紧密堆积；阴离子小，阳离子大：阴离子按一定方式堆积，阳离子位于堆积产生的空隙之中。离子半径比是决定离子晶体构型的重要因素。
AB型离子晶体：
- CsCl型：简单立方，$\ce{Cs+}$位于晶胞体心，正负离子配位数$8 : 8$，$r_+ / r_- > 0.732$，如RbCl、TlCl等。
- NaCl型：面心立方，$\ce{Cl-}$ccp，$\ce{Na+}$占据全部八面体空隙，正负离子配位数$6 : 6$，$0.414 < r_+ / r_- < 0.732$，如KCl、CaO等。
- 立方ZnS型：$\ce{S^{2-}}$ccp，$\ce{Zn^{2+}}$占据$\frac 1 2$的四面体空隙，正负离子配位数$4 : 4$，$r_+ / r_- > 0.414$，如CuCl、ZnO等。
$\ce{AB2}$型离子晶体：
- 萤石（$\ce{CaF2}$）：$\ce{F-}$ccp，$\ce{Ca^{2+}}$占据全部四面体空隙。
- 金红石（$\ce{TiO2}$）：$\ce{O^{2-}}$畸变的hcp，Ti占据$\frac 1 2$八面体空隙，每层中交替占据，形成正方形孔道。
- $\ce{CdCl2}$：$\ce{Cl-}$ccp，$\ce{Cd^{2+}}$占$\frac 1 2$八面体空隙，满占层和空占层交替，形成层状结构。
分子晶体：共价分子通过分子间作用力形成晶体，常见于气态或液态共价分子凝固成的固体。通常采取密堆结构以增强分子间作用力。
- $\ce{CO2}$晶体：通过vdW作用力形成。
- 冰的晶体：通过氢键作用力形成。
共价晶体（原子晶体）：通过共价键连接成三维结构，整个晶体相当于一个大分子。一般不采取密堆结构，具有熔点高、硬度大等特点。
- 金刚石晶体：碳原子占据立方体顶点、面心和$\frac 1 2$的四面体空隙，形成完美正四面体连接。类似结构：Si、Ge、立方BN。
- 石英/沸石：通过$\ce{Si-O}$共价键形成三维网络，其中$\ce{SiO4}$四面体共顶点连接，具有非常丰富的孔道结构。其中Si和O的配位数分别为4和2。
- 金属有机框架（MOF）:金属离子和有机配体通过配位键连接成的三维网络，可形成比表面积非常大的规则多孔结构。
含有多种键型的晶体：
- 石墨：层内共价键，层间vdW力。由共价键构成的二维结构单元通过另一种键合方式形成三维晶体。
- $\ce{KAl2(OH)2Si3AlO10}$：$\ce{SiO4}$四面体构成的$\ce{Si-O}$层，层间插入$\ce{K+}$和$\ce{Al^{3+}}$。

5. 化学键键型和晶体构型的变异

离子的极化：在周围异性电荷离子影响下，电子云发生变形，离子键逐渐向共价键过渡。
- 阳离子正电荷越高，极化能力越强；阴离子体积越大，越容易被极化。
- 具有$\mathrm{d^{10}}$构型的阳离子（$\ce{Ag+}$，$\ce{Cu+}$，$\ce{Zn^{2+}}$，$\ce{Hg^{2+}}$）既有强的极化能力，也有较大的变形性。
电负性对化学键类型的影响：键的离子性 $=$ 实测偶极矩$/($离子电荷$\times$键长$)$ $= 1 - \mathrm{e}^{-(\chi _ A - \chi _ B)^2 / 4}$。

第14章配位化合物

提纲

典型配合物的几何形状和异构现象
配合物的化学键理论：价键理论、晶体场理论、配位场理论
晶体场分裂能、高低自旋、磁性判断、d-d跃迁和配合物的颜色
配合物的应用
配位平衡及其移动，与酸碱、沉淀溶解和氧化还原平衡的综合应用

1. 配位化合物及其组成

配位化合物：中心金属和配体构成的化合物，对中心金属、配体和配合物整体的电性都没有要求。
配合物的中心体通常为过渡金属原子或离子，而配体则是可以提供孤对电子的分子或离子。
单齿配体：只有一个配位原子与中心原子相结合；多齿配体：有两个或以上配位原子与中心原子相结合。
配合物可以分为内界和外界两个部分，中心离子（或原子）与配体共同形成内界，而平衡配离子的电荷离子则称为外界。
螯合物：有一个或多个多齿配体提供多对电子与中心体形成配位键，常比一般配合物要稳定，原因：多个化学键、熵效应。
多齿配体的结构演变：简单螯合→大环→穴合。
配合物的应用：金属的提取、分离和检测；光电转化；催化。

2. 配位化合物的异构现象

配合异构分为结构异构和空间异构两大类。
结构异构是指配合物的基本结构或化学键类型不同的情况，包括电离异构、水合异构、配位异构、键合异构和配体异构等形式。
- 键合异构：用不同的配位原子和中心金属键合。两可配体：$\ce{CN-}$、$\ce{ONO-}$、$\ce{SCN-}$、$\ce{SeCN-}$、$\ce{S2O3^{2-}}$等
空间异构是指配合物种只是配体彼此在空间的相对位置不同的情形，包括几何异构和旋光异构两种。
- 几何异构（平面正方配合物）：$\ce{MA2B2} ~ 2$种［顺式（cis-）、反式（trans-）］，$\ce{MA2BC} ~ 2$种，$\ce{MABCD} ~ 3$种，$\ce{M(AB)2} ~ 2$种。
- 几何异构（八面体配合物）：$\ce{MA6}$和$\ce{MA5B}$只有一种结构，$\ce{MA4B2} ~ 2$种［顺式（cis-）、反式（trans-）］，$\ce{MA3B3} ~ 2$种［经式（mer-）、面式（fac-）］，$\ce{MA2B2C2} ~ 5$种几何异构配合物，其中1个有镜像异构对映体。
- 镜像对映体和手性：物体不能与其镜像完全重合，称为手性。镜像对映体也属于异构体。存在对称面的分子没有镜像对映体。

3. 配合物的价键理论

配合物中心离子与配位体之间通过配位原子孤对电子轨道与中心离子（或原子）的空轨道重叠，两者共享该电子对形成配位键。因此，配位键本质上是共价性质的。
配位键的形成条件：配位体含有孤对电子；中心离子（或原子）具备相应的空轨道。
外轨型配合物（高自旋）：中心离子使用外层杂化轨道，采取$n\mathrm sn\mathrm pn\mathrm d$杂化形式。
- 卤素、氧（如$\ce{H2O}$）等配位原子电负性较高，不易给出孤对电子，倾向于占据中心离子的外轨，而对其内层电子排布几乎无影响。
- 内层d电子尽可能分占每个3d轨道而自旋平行，因此未成对电子数较多，所以这类配合物又被称为高自旋型配合物。
内轨型配合物（低自旋）：中心离子使用内层杂化轨道，采取$(n-1)\mathrm dn\mathrm sn\mathrm p$杂化形式。
- 碳（如$\ce{CN-}$配体以C配位）、氮（$\ce{NO2-}$配体以N配位）等配位体原子电负性较低，容易给出孤对电子，它们在接近中心离子时，对其内层d电子排布影响较大。
- 使中心离子d电子发生重排，电子挤入少数轨道，自旋平行的d电子数目减少，这类配合物又称为低自旋配合物。
配合物的磁矩：物质磁性大小用磁矩表示，磁矩来源于未成对电子。公式：$\mu = \sqrt{n(n+2)} \mu_B$，其中$n$为未成对电子数，$\mu_B$为Bohr磁子（即一个电子自旋产生的磁矩）。适用于d区元素，不适用于f区元素。

4. 晶体场理论

四面体场和八面体场

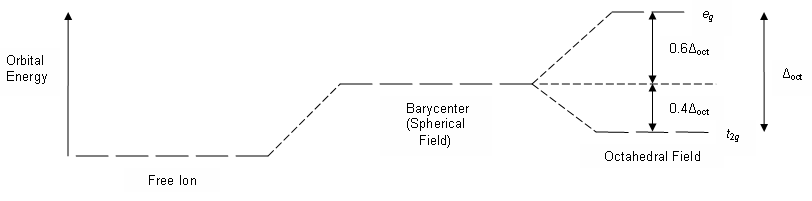
自由离子	球对称负电场 5个d轨道能量等量升高	八面体负电场 5个d轨道能量不等量升高发生分裂

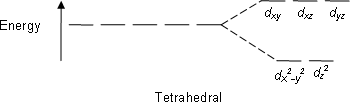
晶体场理论认为配合物中化学键的本质是静电作用：中心离子与配体通过静电吸引而使能量降低，形成成键作用。
过渡金属中心离子的5个d轨道在配位场中能级分裂。d轨道受到周围非球形对称的配位负电场作用时，配位体的负电荷与d轨道中的电子相互排斥，不仅使得各d轨道电子能量普遍升高，而且不同d轨道因受到的影响不一样，各轨道能量升高值不同，从而发生d轨道能级分裂。
能够解释配合物中d电子填充和配合物的光谱。
正八面体配合物：5个d轨道分裂成2组简并的轨道。
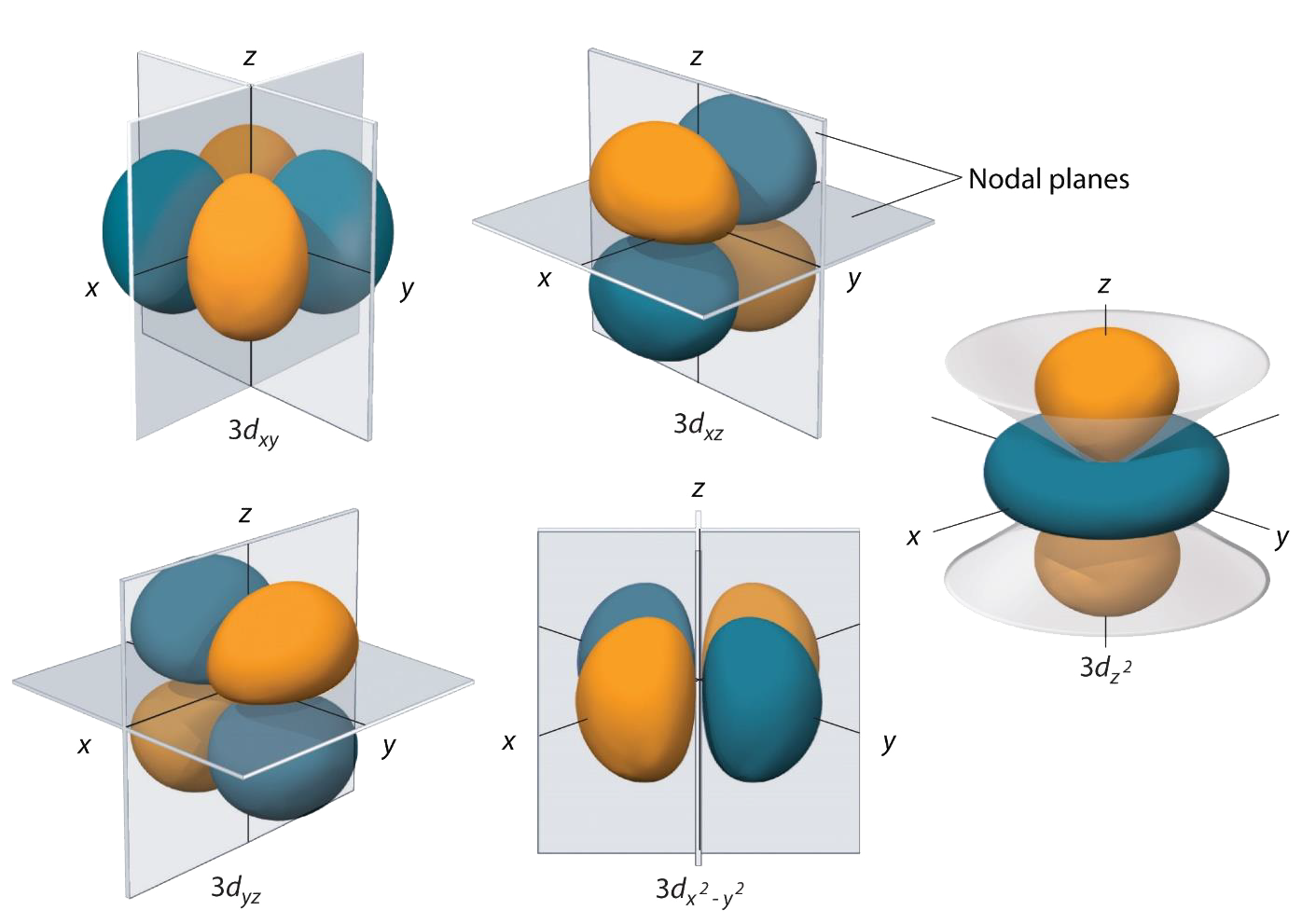
- $\mathrm{e_g}$轨道：$\mathrm d_{x^2-y^2}$和$\mathrm d_{z^2}$受排斥力大，能量高；$\mathrm{t_{2g}}$轨道：$\mathrm d_{xy}$，$\mathrm d_{yz}$，$\mathrm d_{xz}$受排斥力小，能量低。
正四面体配合物：e轨道：$\mathrm d_{x^2-y^2}$和$\mathrm d_{z^2}$受排斥力小，能量低；$\mathrm{t_2}$轨道：$\mathrm d_{xy}$，$\mathrm d_{yz}$，$\mathrm d_{xz}$受排斥力大，能量高。
晶体场分裂能及高低自旋：高低自旋取决于分裂能$\Delta$和电子成对能$P$的相对大小。
- $\Delta_O$：八面体晶体场分裂能，$\mathrm{e_g}$和$\mathrm{t_{2g}}$轨道能量差。
- $\Delta_O > P$：强场低自旋；$\Delta_O < P$：弱场高自旋。$P$约为30 000 cm^-1（3.72 eV）。
- $\Delta_T = \frac 4 9 \Delta_O$。不同对称性的晶体场，d轨道分裂方式和$\Delta$大小均不相同。
影响分裂能的因素：
- 中心离子：同一种构型的配合物，分裂能的大小与中心金属种类、价态、在周期表中的位置有关。一般的，中心离子电荷越高，半径越大，分裂能也越大。
- 配体：对于同种构型、同一中心金属离子的配合物，分裂能与配位体的电荷或偶极矩密切相关。对不同的中心金属该顺序略有差别，大体上以$\ce{H2O}$和$\ce{NH3}$作为分界，区分“强场配体”和“弱场配体”。

\[\ce{I− < Br− < S2− < SCN− < Cl− < NO3− < N3− < F− < OH− < C2O4^{2−} \\ < H2O < NCS− < CH3CN < py < NH3 < en < 2,2'-bipy < phen \\ < NO2− < PPh3 < CN− < CO}.\]

配合物的颜色：d轨道分裂能$\Delta$相当于可见光的能量。在白光照射下，电子吸收其中部分可见光能量，发生$\mathrm{t_{2g} \to e_g}$的跃迁，称为d-d跃迁。吸收波长和配合物颜色与分裂能相关。
能量单位的换算：光谱学中常用波数（定义为波长的倒数，单位$\pu{cm-1}$）作为能量单位，H的第一电离能用波数表示就是Rydberg常数。

5. 价键理论和晶体场理论对比

配位键的本质到底是什么？
- 价键理论：共价键；晶体场理论：静电相互作用。
高自旋配合物（如$\ce{FeF6^{3-}}$）：
- 价键理论：配体电子填入4d轨道，$\mathrm{sp^3d^2}$；晶体场理论：没有用4d轨道，3d轨道不参与成键，但发生能级分裂。
低自旋配合物（如$\ce{Fe(CN)6^{3-}}$）：
- 价键理论：配体电子填入3d轨道，$\mathrm{d^2sp^3}$；晶体场理论：配体电子没有填入3d轨道，3d轨道不参与成键，但发生能级分裂。
两种理论都可以解释配合物的磁性，但价键理论不能解释配合物的颜色。
配位键显然不是静电性的，有显著的饱和性和方向性，CO、$\ce{NH3}$等中性分子配位作用强于带负电的卤素离子。
配位场理论：基于分子轨道理论改进的晶体场理论，配位键成键同时考虑静电作用和共价作用，同时继承了晶体场理论对d轨道分裂的处理方法。

6. 配位平衡及其应用

稳定常数：$K_稳 = \cfrac {[\ce{ML_n}]} {[\ce{M}][\ce{L}]^n}$。实际应用中配体常过量，累积稳定常数更常用。
配位平衡与酸碱平衡：弱酸根、胺（氨）类配体，改变pH会影响配位平衡。定性判断：提高pH，有利于弱酸根配合物生成，不利于胺（氨）类配合物生成。
配位平衡与沉淀溶解平衡：配合物/沉淀，配合物/配合物之间的转化反应。
配位平衡与氧化还原平衡：配合物生成影响金属离子浓度，从而影响金属离子的电极电势。

第15章元素化学

1. s区元素

价电子构型：$n\mathrm s^{1-2}$，典型活泼金属，易形成离子化合物。碱金属、碱土金属。
从上至下，原子半径、离子半径依次增大，电离能依次减小。
与水反应：碱金属与水激烈反应，生成的氢气能自燃；碱土金属与水反应不如碱金属剧烈。
氢氧化物酸碱性的定性与半定量判断：
- 两种断裂方式：碱式$\ce{R-O-H -> R+ + OH-}$，酸式$\ce{R-O-H -> R-O- + H+}$。以何种方式断裂取决于R与O的连接强度。
- 离子势：$\varphi = Z/r$，衡量R对O的吸引能力强弱。
- $\sqrt \varphi > 0.32$，对O吸引强，电离出$\ce{H+}$，酸性；$\sqrt \varphi < 0.22$，对O吸引弱，电离出$\ce{OH-}$，碱性。$0.22 < \sqrt \varphi < 0.32$，酸碱式均可，两性。
在一定条件下，$\mathrm {I_A}$、$\mathrm {II_A}$族金属皆可生成过氧化物（Be除外）：
- Na在加压氧气中燃烧可以进一步形成超氧化钠$\ce{NaO2}$，K、Rb、Cs在空气中燃烧就可以形成超氧化物$\ce{MO2}$。
- 过氧化物中含有过氧离子$\ce{O2^{2-}}$，其中O的氧化数为-1。超氧化物中含超氧离子$\ce{O2-}$，其中O的氧化数为$-\frac 1 2$。
- 过氧化物和超氧化物都是强氧化剂；与$\ce{H2O}$或$\ce{CO2}$反应可放出氧气，用作供氧剂。
在周期表中，尤其是主族元素，各族的第一个元素往往与同族其它元素的性质差别显著，这就是第二周期元素性质的特殊性。
- 对角规则：一个元素与其次周期次族的元素性质相似，如：Li与Mg、Be与Al、B与Si等。正离子的电荷越多，其极化能力越强，而半径越大，极化能力则越弱。两种效应在对角上互相抵消，导致对应的元素性质相似。
碱金属的活泼性由上至下依次增加，但$\ce{Li+/Li}$的电极电势最低。虽然锂的第一电离能较高，但所形成的$\ce{Li+}$半径小，极化能力强，水合作用较强。$\ce{Li+/Li}$的低电势和Li较小的原子量使锂电池具有较高的能量密度。
碱金属和碱土金属能溶于液氨生成蓝色溶液，随着金属溶解的量增加，溶液的颜色变深，超过1 mol/L则为青铜色。
H的成键性质：
- 像碱金属：失去价电子形成$\ce{H+}$离子。
- 像卤素：结合一个电子形成负氢离子$\ce{H-}$，$\ce{H-}$半径较大，容易变形。
- 像碳：氢与大多数非金属元素化合时形成共价型化合物。氢的电负性为2.20，高于多数元素，因此除卤素、氧、氮等少数几种元素外，氢与其他元素所成共价键中氢都带负电性。

2. p区元素

价电子构型：$n\mathrm p^{1-6}$，具有丰富的氧化态。
不同单质的同素异形体：
- 金属：堆积形式不同产生同素异形体，如立方Co和六方Co。
- p区元素：通过共价键形成团簇，团簇之间进一步通过相互作用形成固体。p区各族之间的成键形式有显著差别。
13 ~ 15族类金属元素与碱金属形成的化合物中通常含有多聚阴离子团簇，称为Zintl化合物，不符合通常的化合价原理。
随周期升高，同族氢化物稳定性降低。
EHn的化学性质：
- H的酸性：$\ce{EH_n -> EH_{n-1} + H+}$，$\ce{E = F, Cl, Br, I; O, S, Se, Te; N}$。
- E的碱性：$\ce{EH_n + H+ -> EH_{n+1}+}$，$\ce{E = N, P, O}$。
- H的碱性：$\ce{EH_n + HX -> EX_n + H2}$，$\ce{E = B, Al, Si, Sn}$等低电负性元素，$\ce{X= -OH}$，卤素。
卤化物中性分子多数为气体、易挥发的液体或固体。
不同电性基团之间的复分解反应：X、$\ce{-OH}$、$\ce{-OR}$、$\ce{-NH2}$等均为电负性的一价基团，在适当条件下可以发生取代，形成结构类似的化合物。
最高价含氧酸结构相似，均为四面体结构。同一原子上连接了大量$\ce{-OH}$时易发生分子内脱水。
- 酸性强弱判断：设含氧酸的通式为$\ce{MO_m(OH)_n}$，非羟基氧越多，含氧酸的酸性越强。
Lewis酸碱理论：$\ce{A + :B -> A:B}$。
- Lewis酸：电子对受体；13族，过渡金属；Lewis碱：电子对给体；15 ~ 17族。
- Lewis酸碱理论（电子对酸碱理论）包含了质子酸碱理论。
超强酸：酸性显著超过常见的强酸浓水溶液的体系。超强碱：接受质子能力显著超过$\ce{OH-}$的体系。超强酸碱均为非水体系。
软硬酸碱原理
- 硬酸：碱金属、碱土金属、$\ce{H+}$、高价的金属离子；半径小，电荷高，氧化态增高，硬度加大。软酸：重过渡金属离子，低价或零价金属。半径大、电荷低。
- 硬碱：半径小，不易被极化。软碱：半径大，易被极化。
- 软亲软、硬亲硬：软酸与软碱、硬酸与硬碱结合力强。前者共价作用，后者静电作用。
振荡反应：存在自催化过程的复杂反应中，一些中间产物浓度会发生周期性的非单调变化，多见于卤素体系。

3. d区元素

价电子构型：$(n-1)\mathrm d^{1\text{ ~ }10} n\mathrm s^2$，具有丰富的氧化态。
d区元素的原子半径变化显著小于同周期s区元素：电子填入内层轨道，对半径贡献变小。
- 同周期半径逐渐减小：d区收缩。
- 从10至13族又开始增大：d轨道充满后，外层电子间排斥力增大。
- 随周期数增加原子半径趋向增加，但4d与5d的差别很小：镧系收缩。
金属的熔点变化：金属的熔点越高，金属键越强，熔点最高的金属在第6族。同一族金属，随周期数升高，d区熔点升高，s区熔点降低。
d区元素的金属键：
- 可以成键的轨道：$(n-1)\mathrm d + n\mathrm s$，共6个轨道
- 第6族金属键最强：价电子数 = 6时，键级达到最大
- 高周期金属键更强：4d、5d轨道更加扩展，成键能力：5d > 4d > 3d。
金属合金——固溶体：
- 取代型固溶体：由另一种原子取代原有金属位点，并呈自由分布。形成条件：半径、晶体结构和电负性相近。
- 间隙型固溶体：较小的原子（$\ce{H, B, C, N}$等）置于原有金属晶格位点的空隙中，可形成整比或非整比化合物。
金属合金——金属间化合物：原子呈长程周期性排列，结构可能与其组分完全不同。常见于原子半径和电负性差别较大的金属之间。
d区元素的氧化还原性能：d区元素具有丰富的氧化还原行为和中间价态，可利用电势图判断价态的稳定性（氧化性、还原性、岐化稳定性）。
在水溶液中的稳定性：$\varphi^\ominus_{(\ce{H+/H2})} < \varphi^\ominus < \varphi^\ominus_{(\ce{O2/H2O})}$。
d区元素最高价氧化态的氧化性：3d > 4d > 5d。$n$值较大时，$n\mathrm d$轨道更加扩展，易于成键。3d更像内层电子，5d更像价电子。高周期元素更容易得到高价态：$\ce{FeO4^{2-}, RuO4, OsO4}$。
d区元素与主族元素相似性：$n\mathrm s^{1\text{ ~ }2}$与$(n-1)\mathrm d^{10} n\mathrm s^{1\text{ ~ }2}$元素的离子，电荷相同、离子半径相似。14 ~ 16族元素与下一周期4 ~ 6族元素（$Z \text{ ~ } Z + 8$）：最高价氧化物、含氧酸性质类似。
多酸：最高价含氧酸脱水缩合的产物。酸性越强，越有利于多酸形成。
金属羰基化合物：CO中的孤对电子向金属空轨道配位，$\mathrm p^*$轨道接收金属d轨道中的电子。CO为$\sigma$给体、$\pi$受体，为强场配体。
过渡金属在催化中的应用：氧化还原、活化惰性化学键等催化特性与d区元素变价特性和d轨道成键特点密切相关。

4. 镧系元素

电子构型：[Xe]4f^{0 ~ 14}5d^{0 ~ 1}6s²。
- 4f电子：内层电子，绝大多数情况下难以参与成键。
- 镧系元素基本特点：相似性、镧系收缩。
常用符号：Ln：镧系元素；RE：稀土元素（镧系+ Y + Sc）；Mm：混合稀土。
镧系元素原子和离子半径变化趋势——镧系收缩：相邻收缩小，累计效应大。结果：4d、5d元素原子半径相近。
稀土资源的利用：绿色、高值、均衡利用。稀土元素是重要的战略资源：稀土永磁、稀土发光、稀土储氢、稀土催化。

第2章 气体

提纲