《计算概论（B）》（马思伟）作业参考代码（2017）

这是2017年秋季学期《计算概论（B）》（主讲：马思伟）课程作业的参考代码，仅供学习交流，切勿抄袭。

作业2

1. 与3无关的数

(1) 题目要求

描述

一个正整数，如果它能被3整除，或者它的十进制表示法中某个位数上的数字为3，则称其为与3相关的数。现给定一个正整数$n$（$n < 100$），判断$n$是否是与3相关的数。

关于输入

输入为一行，正整数$n$，$n < 100$。

关于输出

输出为一行，如果$n$为与3相关的数，则输出TRUE，否则输出FALSE。

例子输入

例子输出

FALSE
FALSE
TRUE
TRUE
TRUE
TRUE

(2) 参考答案

#include <stdio.h>

int main() {
    int i;
    for (i = 0; i < 6; i++) {
        int a;
        scanf("%d", &a);
        if (!(a % 3) || (a % 10 == 3) || (a / 10 == 3)) {
            printf("TRUE\n");
        }
        else {
            printf("FALSE\n");
        }
    }
}

(3) 说明

这个题说明和实际不一样……实际上要输入六次、输出六次，因此需要一个循环。

2. 判断闰年

(1) 题目要求

描述

判断某年是否是闰年。

关于输入

输入只有一行，包含一个整数$a$（$0 < a < 3000$）。

关于输出

一行，如果公元$a$年是闰年输出Y，否则输出N。

例子输入

例子输出

FALSE

(2) 参考答案

#include <stdio.h>

int main() {
    int a;
    scanf("%d", &a);
    if ((a % 4) || (!(a % 100) && (a % 400))) {
        printf("N");
    }
    else {
        printf("Y");
    }
}

(3) 说明

闰年的定义不要忘……能被4整除但不能被100整除，或能被400整除的年份即为闰年。

3. 数组逆序

(1) 参考答案

#include <stdio.h>

int main() {
    int a, i;
    int b[100];
    scanf("%d", &a);
    for (i = 0; i < a; i++) {
        scanf("%d", &b[i]);
    }
    for (i = 0; i < a; i++) {
        printf("%d", b[a - i - 1]);
        if (i < a - 1) {
            printf(" ");
        }
    }
}

(2) 说明

注意输出时的空格，只有前$n - 1$项需要输出空格，最后一项不需要。此代码最后一部分也可以写成：

for (i = 0; i < a - 1; i++) {
    printf("%d ", b[a - i - 1]);
}
printf("%d", b[0]);

4. 逆序输出整数

(1) 参考答案1

#include <stdio.h>

int main() {
    int i;
    int a;
    scanf("%d", &a);
    do {
        printf("%d", a % 10);
        a = a / 10;
    } while (a > 0);
}

(2) 参考答案2

#include <stdio.h>

int main() {
    int i;
    char b[10] = { 0 };
    scanf("%s", b);
    for (i = 9; i > -1; i--) {
        if (b[i] > 32) {
            printf("%c", b[i]);
        }
    }
}

(3) 说明

注意考虑输入的数为1000时的输出。如果直接计算出倒序的数字，则输出时前面会缺少0，即输出为1而不是0001。

5. 人民币支付

(1) 题目要求

描述

从键盘输入一指定金额（以元为单位，如345），然后输出支付该金额的各种面额的人民币数量，显示100元，50元，20元，10元，5元，1元各多少张，要求尽量使用大面额的钞票。

关于输入

一个小于1000的正整数。

关于输出

输出分行，每行显示一个整数，从上到下分别表示100元，50元，20元，10元，5元，1元人民币的张数。

例子输入

例子输出

(2) 参考答案

#include <stdio.h>

int main() {
    int a;
    int i;
    int b[6] = { 100, 50, 20, 10, 5, 1 };
    scanf("%d", &a);
    for (i = 0; i < 6; i++) {
        printf("%d\n", a / b[i]);
        a = a % b[i];
    }
}

6. 其他心得

最好在if()、while()、for()等条件后加{}，即使执行的语句只有一句话，否则需要修改程序时可能会忘记。
scanf()里面一定要有&，printf()里面一定不要有&（仅对目前来说）。

作业3

1. 二维数组回形遍历

(1) 题目要求

描述

给定一个row行col列的整数数组array，要求从array[0][0]元素开始，按回形从外向内顺时针顺序遍历整个数组。如所示：

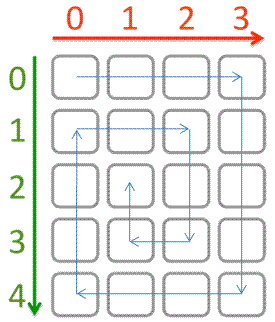
关于输入

输入的第一行上有两个整数，依次为row和col。

余下有row行，每行包含col个整数，构成一个二维整数数组。

（注：输入的row和col保证0 < row < 100，0 < col < 100）

关于输出

按遍历顺序输出每个整数。每个整数占一行。

例子输入

例子输出

(2) 参考答案

#include <stdio.h>

int main() {
    int a[100][100]; //定义数组a存放给定数组
    int i, j;
    int row, col;
    scanf("%d %d", &row, &col); //输入行、列
    for (i = 0; i < row; i++) {
        for (j = 0; j < col; j++) {
            scanf("%d", &a[i][j]); //输入数组内容
        }
    }
    int b[100][100] = { 0 }; //定义数组b存放该整数是否已被输出，未输出为0，已输出不为零
    i = 0;
    j = 0;
    int k = 0; //定义已经被输出的数字的个数
    do {
        while (!b[i][j] && j < col) { //如果a[i][j]没有被输出，且j<col则继续输出
            printf("%d\n", a[i][j]);
            b[i][j++] = ++k; //将a[i][j]设置为已输出，同时j+1
        }
        j--; //改变输出方向
        i++;
        while (!b[i][j] && i < row) {
            printf("%d\n", a[i][j]);
            b[i++][j] = ++k;
        }
        i--;
        j--;
        while (!b[i][j] && ~j) {
            printf("%d\n", a[i][j]);
            b[i][j--] = ++k;
        }
        j++;
        i--;
        while (!b[i][j] && ~i) {
            printf("%d\n", a[i][j]);
            b[i--][j] = ++k;
        }
        i++;
        j++;
    } while (k < row * col); //判断是否所有数都已输出
}

(3) 说明

这个题目我没有想出较为简单的方法，网络上有的方法也与此方法大致相同，即依次按照“右→下→左→上”的顺序输出。

2. 矩阵乘法

(1) 题目要求

描述

根据矩阵乘法的原理，求出两个矩阵相乘后的新矩阵。

这里我们假定矩阵中每个元素都是正整数。

关于输入

第一行有三个正整数$a$，$b$，$c$（$a, b, c < 500$）。

接下来$a$行，每行$b$个整数，是左矩阵。

接下来$b$行，每行$c$个整数，是右矩阵。

关于输出

输出结果矩阵，共$a$行$c$列，同一行用空格分隔，每一行末尾不能有空格。

例子输入

例子输出

14 32
32 77

(2) 参考答案

#include <stdio.h>

int main() {
    int a, b, c;
    int A[500][500]; //定义A存放左矩阵
    int B[500][500]; //定义B存放左矩阵
    int i, j, k;
    scanf("%d %d %d", &a, &b, &c);
    for (i = 0; i < a; i++) {
        for (j = 0; j < b; j++) {
            scanf("%d", &A[i][j]);
        }
    }
    for (i = 0; i < b; i++) {
        for (j = 0; j < c; j++) {
            scanf("%d", &B[i][j]);
        }
    }
    for (i = 0; i < a; i++) {
        for (j = 0; j < c; j++) {
            int sum = 0;
            for (k = 0; k < b; k++) {
                sum += A[i][k] * B[k][j];
            }
            printf("%d", sum);
            if (j < c - 1) {
                printf(" ");
            }
        }
        printf("\n");
    }
}

(3) 说明

关于矩阵乘法：设$A$为$m\times p$的矩阵，$B$为$p\times n$的矩阵，那么称$m\times n$的矩阵$C$为矩阵$A$与$B$的乘积，记作$A\times B$，其中矩阵$C$中的第$i$行第$j$列元素可以表示为：

\[(AB)_{ij}=\sum_{k=1}^pa_{ik}b_{kj}=a_{i1}b_{1j}+a_{2k}b_{2j}+\cdots+a_{ip}b_{pj}.\]

3. 数组循环右移

(1) 题目要求

描述

有一个整数数组，现要求实现这个整数数组的循环右移。如：1，2，3，4，5；则循环右移两位后结果是：4，5，1，2，3。

关于输入

首先第一行输入数组元素个数$N$，$N$应该不超过50（$N \le 50$）。

接下来输入这个数组的各个元素的值，假定数组值都为整数。

最后换行输入循环右移的位数，要求为正整数。

关于输出

输出为数组循环右移$n$位后的结果。

例子输入

5
1 2 3 4 5
2

例子输出

4 5 1 2 3

(2) 参考答案

#include <stdio.h>

int main() {
    int a[50]; //定义a存放数组
    int n;
    scanf("%d", &n);
    int i;
    for (i = 0; i < n; i++) {
        scanf("%d", &a[i]);
    }
    int b;
    scanf("%d", &b);
    b %= n; //求b÷n的余数
    int c[50];
    int j = 0; //定义为数组c已有的数
    for (i = n - b; i < n; i++) { //将数组a的后半部分存入数组c
        c[j++] = a[i];
    }
    for (i = 0; i < n - b; i++) { //将数组a的前半部分存入数组c
        c[j++] = a[i];
    }
    for (i = 0; i < n; i++) {
        printf("%d", c[i]);
        if (i < n - 1) {
            printf(" ");
        }
    }
}

4. Fibonacci数列

(1) 题目要求

描述

菲波那契数列是指这样的数列: 数列的第一个和第二个数都为1，接下来每个数都等于前面2个数之和。

给出一个正整数$a$，要求菲波那契数列中第$a$个数是多少。由于数值可能比较大，所以只要输出这个数除以10000的余数。

关于输入

输入共一行，一个正整数$a$（$1 \le a \le 100000$）。

关于输出

一行，一个整数，即数列第$a$项除以10000的余数。

例子输入

例子输出

(2) 参考答案

#include <stdio.h>

int main() {
    int a;
    scanf("%d", &a);
    int b = 1, c = 1;
    int i;
    for (i = 0; i < a - 2; i++) {
        b += c;
        c = b - c;
        if (b > 10000) { b -= 10000; }
        if (c > 10000) { c -= 10000; }
    }
    printf("%d", b);
}

5. 学生成绩统计

(1) 题目要求

描述

用结构体数组设计程序：输入5个学生的姓名和4门功课的成绩，输出每个学生的总分，以及总分最低的学生的姓名和总分。

关于输入

5个学生的姓名和4门功课的成绩

关于输出

每个学生的总分，以及总分最低的学生的姓名和总分

例子输入

Sam 90 80 92 78
Tom 78 98 88 87
Jane 97 92 89 78
Joe 67 78 76 80
Dan 90 92 95 89

例子输出

Sam 340
Tom 351
Jane 356
Joe 301
Dan 366
Joe 301

(2) 参考答案

#include <stdio.h>

int main() {
    char a[5][4]; //定义数组a存放名字
    int b[5][3]; //定义数组b存放成绩
    int i;
    int min = 65535; //定义最小值，此处将赋初值为65535
    char* mina; //定义最小值者的名字
    int sum;
    for (i = 0; i < 5; i++) {
        scanf("%s %d %d %d %d", a[i], &b[i][0], &b[i][1], &b[i][2], &b[i][3]);
        sum = b[i][0] + b[i][1] + b[i][2] + b[i][3];
        printf("%s %d\n", a[i], sum);
        if (sum < min) {
            min = sum;
            mina = a[i];
        }
    }
    printf("%s %d", mina, min);
}

(3) 说明

这道题用到了字符型变量（char）和字符串，可以参考《C程序设计》的6.3节的内容。
~~偷懒写法~~：

#include <stdio.h>

int main() {
    printf("Sam 340\n");
    printf("Tom 351\n");
    printf("Jane 356\n");
    printf("Joe 301\n");
    printf("Dan 366\n");
    printf("Joe 301\n");
}

作业4

1. 字符统计与删除

(1) 题目要求

描述

编写自定义函数，该函数可以统计任意一个字符在一个字符串中出现的次数，并将该字符从字符串中删除。如：字符h在字符串hello中出现一次，删除h后的字符串变成ello。

关于输入

先输入一个字符串（长度不超过100），再输入一个字符

关于输出

两行输出，第一行显示字符出现的次数，第二行显示删除该字符后的字符串。

例子输入

hello world!
l

例子输出

3
heo word!

(2) 参考答案

#include <stdio.h>

int main() {
    char a[100];
    char b;
    int c = 0;
    int i;
    gets(a);
    b = getchar();
    for (i = 0; a[i]; i++) {
        if (a[i] == b) {
            c++;
        }
    }
    printf("%d\n", c);
    for (i = 0; a[i]; i++) {
        if (a[i] != b) {
            putchar(a[i]);
        }
    }
}

2. 大整数加法

(1) 题目要求

描述

求两个不超过200位的非负整数的和。

关于输入

有两行，每行是一个不超过200位的非负整数，不会存在多余的前导0。

关于输出

一行，即相加后的结果。结果里不能有多余的前导0，即如果结果是77，那么就不能输出为077。

例子输入

22222222222222222222
33333333333333333333

例子输出

55555555555555555555

提示

由于一个int型整数只能表示-2³¹（-2,147,483,648）到2³¹ - 1（2,147,483,647）之间的整数，所以直接读入再相加是不可行的。

联想到最开始学加法时使用的方法，对于两个数$A = \overline{A_1A_2A_3}$，$B = \overline{B_1B_2B_3}$，我们会通过竖式的方式进行计算：

\[\begin{array}{cc} & A_1 & A_2 & A_3 \\ & B_1 & B_2 & B_3 \\ \hline C_0 & C_1 & C_2 & C_3 \end{array}\]

即将个位、十位、百位对应相加，当然需要考虑进位问题，如果$A_1 + B_1 \ge 10$，就可能产生进位$C_0$。

那么现在对于两个很大的整数，可以利用同样的思路，将一个大整数用一个int数组表示，数组中的每一个元素表示大整数中的某一位。然后通过循环依次将每一位相加（并处理进位），最后的结果放在一个新数组里。

需要注意的是，读入需要将大整数作为一个字符串来读入。

(2) 参考答案

#include <stdio.h>
#include <string.h>

int main() {
    char a[200], b[200];
    int c[201] = {0};
    gets(a);
    gets(b);
    int x, y;
    int i, j = 0;
    int max = strlen(a) > strlen(b) ? strlen(a) : strlen(b);
    for (i = 0; i < max; i++) {
        x = i < strlen(a) ? a[strlen(a) - i - 1] - '0': 0;
        y = i < strlen(b) ? b[strlen(b) - i - 1] - '0': 0;
        c[i] += x + y;
        j = 0;
        while (c[i + j] > 9) {
            c[i + j] %= 10;
            c[i + (++j)]++;
        }
    }
    max = i + j;
    for (i = max - 1; i > -1; i--) {
        putchar(c[i] + 48);
    }
}

3. 蛇形填充数组

(1) 题目要求

描述

用数字1，2，3，4，…蛇形填充规模为$n \times n$的方阵，蛇形填充规则见示例数组。

关于输入

输入为一行，为一个整数$n$，表示输出方阵的行数（$n \le 15$）。

关于输出

输出该方阵，相邻两个元素之间用空格间隔，每行最后一个元素后面没有空格。

例子输入

例子输出

(2) 参考答案

#include <stdio.h>

int main() {
    int a, b;
    int c[100][100];
    int i, j, k = 0;
    scanf("%d", &a);
    for (i = 0; i < 2 * a; i++) {
        for (j = 0; j <= i; j++) {
            if ((i - j < a) && (j < a)) {
                if (i % 2) {
                    c[j][i - j] = ++k;
                } else {
                    c[i - j][j] = ++k;
                }
            }
        }
    }
    for (i = 0; i < a; i++) {
        for (j = 0; j < a; j++) {
            printf("%d", c[i][j]);
            if (j < a - 1) {
                putchar(' ');
            }
        }
        putchar('\n');
    }
}

4. 展开数组

(1) 题目要求

描述

去年阿福做了一个填充数组的任务，至今自己还津津乐道。现在他又遇到了一个相似的问题，跟去年的有那么一点像。可是他平时光顾着自己吹牛，却忘记了那个问题当时是怎么解决的，想请你帮忙回忆一下，到底该怎么做呢？问题如下：以所示的顺序遍历给定的数组。

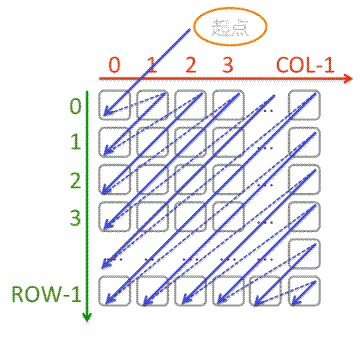
关于输入

输入的第一行上有两个整数，依次为row和col。

余下有row行，每行包含col个整数，构成一个二维整数数组。

（注：输入的row和col保证0 < row < 100, 0 < col < 100）

关于输出

按遍历顺序输出每个整数。每个整数占一行。

例子输入

例子输出

(2) 参考答案

#include <stdio.h>

int main() {
    int a, b;
    int c[100][100];
    int i, j, k;
    scanf("%d %d", &a, &b);
    for (i = 0; i < a; i++) {
        for (j = 0; j < b; j++) {
            scanf("%d", &c[i][j]);
        }
    }
    for (i = 0; i < 2 * (a > b ? a: b); i++) {
        for (j = 0; j <= i; j++) {
            if ((i - j < b) && (j < a)) {
                printf("%d\n", c[j][i - j]);
            }
        }
    }
}

5. 九九乘法表

(1) 题目要求

描述

按照输出的模板，把九九乘法表输出。

关于输入

无

关于输出

1*1= 1

1*2= 2 2*2= 4

1*3= 3 2*3= 6 3*3= 9

1*4= 4 2*4= 8 3*4=12 4*4=16

1*5= 5 2*5=10 3*5=15 4*5=20 5*5=25

1*6= 6 2*6=12 3*6=18 4*6=24 5*6=30 6*6=36

1*7= 7 2*7=14 3*7=21 4*7=28 5*7=35 6*7=42 7*7=49

1*8= 8 2*8=16 3*8=24 4*8=32 5*8=40 6*8=48 7*8=56 8*8=64

1*9= 9 2*9=18 3*9=27 4*9=36 5*9=45 6*9=54 7*9=63 8*9=72 9*9=81

例子输入

例子输出

1*1= 1
1*2= 2  2*2= 4
1*3= 3  2*3= 6  3*3= 9
1*4= 4  2*4= 8  3*4=12  4*4=16
1*5= 5  2*5=10  3*5=15  4*5=20  5*5=25
1*6= 6  2*6=12  3*6=18  4*6=24  5*6=30  6*6=36
1*7= 7  2*7=14  3*7=21  4*7=28  5*7=35  6*7=42  7*7=49
1*8= 8  2*8=16  3*8=24  4*8=32  5*8=40  6*8=48  7*8=56  8*8=64
1*9= 9  2*9=18  3*9=27  4*9=36  5*9=45  6*9=54  7*9=63  8*9=72  9*9=81

(2) 参考答案

#include <stdio.h>

int main() {
    int i, j, c;
    for (i = 1; i < 10; i++) {
        for (j = 1; j <= i; j++) {
            if (j == i) {
                printf("%d*%d=%2d\n", j, i, i * j);
            } else {
                printf("%d*%d=%2d  ", j, i, i * j);
            }
        }
    }
}

(3) 说明

此题在系统中未录入，提交后显示NoTestData。

6. 人民币支付

此题与作业2第5题重复。

7. 字符串子串判断

(1) 题目要求

描述

输入为两个字符串s1和s2（其中串内不包含空格，以空格分开），判断s2是否为s1的子串。如果是，输出true；如果不是，输出false。

子串的意思为：从s1的某个位置开始的一个连续串。

比如：输入ababc abc，输出true；输入ababc abac，输出false。

关于输入

两个不包含空格的字符串s1和s2，以空格分开。

关于输出

判断s2是否为s1的子串。如果是，输出true；如果不是，输出false。

例子输入

ababc abc

例子输出

true

提示

此题是一个很经典的题目，一般的做法需要二重循环来判断。第一重循环变量$i$从s1的头部遍历到尾部，第二重循环从$i$开始判断s1的每个字符是否与s2匹配。

这个算法需要$n \times m$数量级的运算（$n$为s1的长度，$m$为s2的长度），一个更好的方法能够在$n + m$数量级的运算搞定，即KMP算法。

有能力的同学请实现KMP，用一般的方法也可以通过本题的测试样例。

(2) 参考答案1

#include <stdio.h>
#include <string.h>

int main() {
    char str[100],
    par[100]; //定义原字符串和子字符串
    scanf("%s %s", str, par);
    int i, j;
    int strLen = strlen(str),
    parLen = strlen(par); //求出两字符串长度
    for (i = 0; i < strLen - parLen + 1; i++) {
        for (j = 0; j < parLen; j++) {
            if (str[i + j] != par[j]) { //判断两字符是否不同
                break; //若两字符不同则跳出循环
            }
            if (j == parLen - 1) { //判断是否已匹配完成
                printf("true"); //若匹配完成则输出true并结束程序
                return 1;
            }
        }
    }
    printf("false");
    return 0;
}

(3) 参考答案2

#include <stdio.h>
#include <string.h>

int main() {
    char str[100],
    par[100];
    scanf("%s %s", str, par);
    int i = 0, j = 0, m = 0;
    int strLen = strlen(str),
    parLen = strlen(par);
    while (1) {
        while (i < strLen && j < parLen && str[i] == par[j]) {
            i++;
            j++;
            continue;
        }
        if (j == parLen) {
            printf("true");
            return 1;
        } else if (i == strLen) {
            printf("false");
            return 0;
        }
        m = i + parLen - j;
        j = parLen;
        while (j > -1) {
            if (str[m] == par[j]) {
                break;
            }
            j--;
        }
        i += parLen - j;
        j = 0;
    }
}

(4) 说明

此题在系统中未录入，提交后显示NoTestData。
此题中我给出的参考答案1是“暴力匹配法”，是最低级、运算时间最长的算法。提示中所说的“KMP算法”全称为“克努斯-莫里斯-普拉特算法”，可以参考http://blog.csdn.net/v_july_v/article/details/7041827这个链接的内容。

作业5

1. 字符串连接

(1) 题目要求

描述

从键盘输入两个字符串，将第二个字符串连接到第一个字符串后。

关于输入

字符串S1

字符串S2

关于输出

连接后的字符串S1。

例子输入

123
456

例子输出

提示

不能使用strcat()函数。

(2) 参考答案

#include <stdio.h>

int main() {
    char a[100], b[100];
    gets(a);
    gets(b);
    printf(a);
    printf(b);
}

2. 大小写互换

(1) 题目要求

描述

输入一行字符串（带空格），将其中字符的大小写互换。

关于输入

一行字符串，总长度不超过100。

关于输出

输出为1行，输出经过大小写互换之后的字符串。

例子输入

LiFe iS liKe a BoX oF cHocOLate

例子输出

lIfE Is LIkE A bOx Of ChOColATE

(2) 参考答案

#include <stdio.h>

int main() {
    char a[100];
    gets(a);
    int i;
    for (i = 0; a[i]; i++) {
        if (a[i] >= 'a' && a[i] <= 'z') {
            putchar(a[i] + 'A' - 'a');
        }
        else if (a[i] >= 'A' && a[i] <= 'Z') {
            putchar(a[i] + 'a' - 'A');
        }
        else {
            putchar(a[i]);
        }
    }
}

3. 回文字符串

(1) 题目要求

描述

回文就是正读和反读都一样的字符串,例如radar，a man, a plan, a canal, panama（忽略空格和标点符号）。请编写程序，读入一行字符串，若为回文，则输出true，否则输出false。

关于输入

输入有若干行，每行一个字符串，长度不超过100。

关于输出

对应于每一行输入，输出true或false。

注意：忽略字符串中的空格和标点符号。

例子输入

radar
  ,  rada     .'" r
radAr

例子输出

true
true
false

(2) 参考答案

#include <stdio.h>
#include <string.h>

int main() {
    char a[100];
    while (gets(a)) {
        int len = strlen(a);
        int i = 0, j = len - 1;
        while (i <= j) {
            while ((a[i] < 'a' || a[i]>'z') && (a[i] < 'A' || a[i]>'Z') && i < len) {
                i++;
            }
            while ((a[j] < 'a' || a[j]>'z') && (a[j] < 'A' || a[j]>'Z') && j > -1) {
                j--;
            }
            if (a[i] != a[j]) {
                break;
            }
            i++;
            j--;
        }
        if (i <= j) {
            printf("false\n");
        }
        else {
            printf("true\n");
        }
    }
}

4. 数字阶梯求和

(1) 题目要求

描述

给定$a$和$n$，计算$a + \overline{aa} + \overline{aaa} + \overline{a\cdots a}$（$n$个$a$）的和对1000的余数。

关于输入

测试数据有多组。

每组数据一行，分别表示$a$，$n$（$1 \le a \le 9$，$1 \le n \le 100$）。

当输入为两个0的时候，表示输入结束。

关于输出

对于每组输入，请输出结果。每个结果一行。

例子输入

1 10
0 0

例子输出

(2) 参考答案

#include <stdio.h>

int main() {
    int a, n;
    scanf("%d %d", &a, &n);
    while (a && n) {
        int i;
        int s = 0;
        for (i = 0; i < n; i++) {
            switch (i) {
            case 0:
                s += a;
                break;
            case 1:
                s += a * 11;
                break;
            default:
                s += a * 111;
            }
            s %= 1000;
        }
        printf("%d\n", s);
        scanf("%d %d", &a, &n);
    }
}

5. 逆序输出小数

(1) 题目要求

描述

输入一个小数，小数点之前有两位，小数点之后有两位，且小数点之前和小数点之后所有位都不为0，输出小数的逆序。

关于输入

输入一个小数，小数点之前有两位，小数点之后有两位，且小数点之前和小数点之后所有位都不为0。

关于输出

输出小数的逆序。

例子输入

12.34

例子输出

43.21

(2) 参考答案

#include <stdio.h>

int main() {
    int i;
    char b[10] = { 0 };
    scanf("%s", b);
    for (i = 9; i > -1; i--) {
        if (b[i] > 32) {
            printf("%c", b[i]);
        }
    }
}

(3) 说明

此题在系统中未录入，提交后显示NoTestData。

6. 约瑟夫问题

(1) 题目要求

描述

约瑟夫问题：有$n$只猴子，按顺时针方向围成一圈选大王（编号从1到$n$），从第1号开始报数，一直数到$m$，数到$m$的猴子退出圈外，剩下的猴子再接着从1开始报数。就这样，直到圈内只剩下一只猴子时，这个猴子就是猴王，编程求输入$n$，$m$后，输出最后猴王的编号。

关于输入

每行是用空格分开的两个整数，第一个是$n$，第二个是$m$（$0 < m, n \le 300$）。最后一行是：

0 0

关于输出

对于每行输入数据（最后一行除外)，输出数据也是一行，即最后猴王的编号。

例子输入

例子输出

5
1
7

提示

所给的数据中，$m$未必比$n$小！

(2) 参考答案

#include <stdio.h>

int main() {
    int n, m;
    scanf("%d %d", &n, &m);
    while (n && m) {
        int s[301] = { 0 };
        int i = 1, j = 1;
        int k = n - 1;
        while (k) {
            if (j == m) {
                s[i] = 1;
                j = 1;
                k--;
            }
            else {
                j++;
            }
            do {
                if (i == n) {
                    i = 1;
                }
                else {
                    i++;
                }
            } while (s[i]);
        }
        printf("%d\n", i);
        scanf("%d %d", &n, &m);
    }
}

作业6

1. 用函数实现Fibonacci数列

(1) 题目要求

描述

用函数实现Fibonacci数列：0，1，1，2，3，5，8，13，21，……

关于输入

主函数中输入项数$n$。

关于输出

输出Fibonacci数列的第$n$项值。

例子输入

例子输出

提示

必须用函数实现！

(2) 参考答案

#include <stdio.h>

int main() {
    int a;
    scanf("%d", &a);
    int b = 0, c = 1;
    int i;
    for (i = 1; i < a; i++) {
        b += c;
        c = b - c;
    }
    printf("%d", b);
}

(3) 说明

main函数也是函数。

2. 定义求幂的函数

(1) 题目要求

描述

定义函数，它求出一个浮点数$x$的$n$次幂。

关于输入

输入只有一行，先后输入浮点数$x$和整数$n$。

关于输出

输出计算得到的$x$的$n$次幂。

例子输入

1.2 2

例子输出

1.44

提示

注意$n = 0$和$n < 0$的情况。

当$x$和$n$的值比较大时，看看发生浮点数计算溢出时会出现什么情况。

(2) 参考答案

#include <stdio.h>
#include <math.h>

int main() {
    float x;
    int n;
    scanf("%f %n", &x, &n);
    printf("%f", pow(x, n));
}

(3) 说明

此题在系统中未录入，提交后显示NoTestData。

3. 水仙花数

(1) 题目要求

描述

我们知道，如果一个数是水仙花数，当且仅当它的各位数字的三次方的和与这个数相等。

如$153 = 1 ^ 3 + 5 ^ 3 + 3 ^ 3$，则153是水仙花数。

关于输入

输入数据有若干组，每组一个三位数$N$（$100 \le N \le 999$）。

关于输出

每组测试数据一行，如果这个数是水仙花数，则输出Yes，否则输出No。

例子输入

例子输出

Yes

(2) 参考答案

#include <stdio.h>
#include <math.h>

int main() {
    int a;
    while (scanf("%d", &a) > -1) {
        printf(a == (int)(pow(a / 100, 3) + pow(a % 100 / 10, 3) + pow(a % 10, 3)) ? "Yes" : "No");
    }
}

4. 汉诺塔问题（Hanoi Tower）

(1) 题目要求

描述

这是一个流传很久的游戏。

初始状态：有三根杆子A，B，C。A杆上有$n$只碟子。
规则：每次移动一块碟子,小的只能叠在大的上面。
目标：把所有碟子从A杆借助C杆全部移到B杆上。

关于输入

以A杆上的盘子个数作为输入（20以内）。

关于输出

输出将A杆的盘子全部移到B杆需要的最小移动次数。

例子输入

例子输出

提示

使用函数递归的方法进行思考。

(2) 参考答案

#include <stdio.h>
#include <math.h> 

int main() {
    int n;
    scanf("%d", &n);
    printf("%d", (int)pow(2, n) - 1);
}

(3) 说明

此题只要求求出最小移动次数，可以用公式$a_n = 2^n-1$而无需模拟移动过程。
编程网格上另有一题要求输出搬动方案。

5. 求一元二次方程的根

(1) 题目要求

描述

已知一个一元二次方程$ax^2 + bx + c = 0$，其中$a \neq 0$。请利用求根公式编程求解这个一元二次方程的解。

求根公式：两个根分别为$x_1 = \cfrac {-b - \sqrt{b^2 - 4ac}}{2a}$；$x_2 = \cfrac{-b - \sqrt{b^2 - 4ac}}{2a}$。

关于输入

输入共一行，三个实数a, b, c。

关于输出

输出一行，表示方程的解。

若两个实根相等，则输出形式为：x1=x2=...。

若两个实根不等，则输出形式为：x1=...;x2 =...。其中x1 > x2。

若无实根，则输出no solution。

所有实数部分要求精确到小数点后5位，数字、符号之间没有空格。详细格式请看样例。

例子输入

1 3 2

例子输出

x1=-1.00000;x2=-2.00000

提示

求平方根需要使用定义在math.h中的sqrt()函数。sqrt(x)即对x开方。

首先应该在主函数前添加#include <math.h>，然后才能调用该函数。

(2) 参考答案

#include <stdio.h>
#include <math.h>

int main() {
    int a, b, c;
    scanf("%d %d %d", &a, &b, &c);
    int delta = b * b - 4 * a * c;
    if (delta) {
        if (delta > 0) {
            float x1 = (-b + sqrt(delta)) / (2 * a), x2 = (-b - sqrt(delta)) / (2 * a);
            if (x1 > x2) {
                printf("x1=%.5f;x2=%.5f", x1, x2);
            }
            else {
                printf("x1=%.5f;x2=%.5f", x2, x1);
            }
        }
        else {
            printf("no solution");
        }
    }
    else {
        printf("x1=x2=%.5f", -b / (2.0 * a));
    }
}

(3) 说明

此题与作业1第6题重复。

6. 定义求体积或面积的函数

(1) 题目要求

描述

定义求圆球的体积、求圆球的表面积、求圆柱体的体积、求圆柱体的表面积的函数。

关于输入

输入有两行。

第一行包含一个整数$n$，当$n$为1时，求圆球的体积；$n$为2时，求圆球的表面积；$n$为3时，求圆柱体的体积；$n$为4时，求圆柱体的表面积。

在求圆球的体积或表面积时，第二行为一个浮点数，表示圆球的半径。

在求圆柱体的体积或表面积时，第二行为两个浮点数，依次是圆柱的半径和高。

关于输出

输出只有一行，计算出的体积或表面积的值，精确到小数点后4位。

例子输入

1
1.0

例子输出

4.1888

提示

圆球体积公式：$\frac43\times\pi\times r^3$。

(2) 参考答案

#include <stdio.h>
#include <math.h>
#define PI 3.1415927

int main() {
    int n;
    scanf("%d", &n);
    float a, b;
    scanf("%f %f", &a, &b);
    switch (n) {
    case 1:
        printf("%.4f", 4.0 / 3 * PI * a * a * a);
        break;
    case 2:
        printf("%.4f", 4 * PI * a * a);
        break;
    case 3:
        printf("%.4f", PI * a * a * b);
        break;
    case 4:
        printf("%.4f", 2 * PI * a * a + 2 * PI * a * b);
    }
}

作业7

1. 顺序输出三个整数（使用指针完成）

(1) 题目要求

描述

输入三个数（包括整数与浮点数），按由小到大的顺序输出。若输入为整数，则按整数输出；若输出为浮点数，则输出为浮点数，且保留小数点后2位。（请使用参数为指针的函数来完成！！！）

关于输入

输入为三个数，逗号隔开。

关于输出

输出为按由小到大顺序排列的数，用逗号隔开。

例子输入

1,2.8,2

例子输出

1,2,2.80

(2) 参考答案

#include <stdio.h>
void swap(float* x, float* y) {
    float temp;
    temp = *x;
    *x = *y;
    *y = temp;
}

int main() {
    float a[3];
    int i;
    float temp;
    scanf("%f,%f,%f", a, a + 1, a + 2);
    if (*a > * (a + 1)) {
        swap(a, a + 1);
    }
    if (*(a + 1) > * (a + 2)) {
        swap(a + 1, a + 2);
    }
    if (*a > * (a + 1)) {
        swap(a, a + 1);
    }
    for (i = 0; i < 3; i++) {
        if ((int)a[i] == a[i]) {
            printf("%.0f", a[i]);
        }
        else {
            printf("%.2f", a[i]);
        }
        if (i < 2) {
            printf(",");
        }
    }
}

2. 1037 求字符串长度

(1) 题目要求

描述

求一个长度不大于100的字符串的长度，要求不使用strlen方法，并且使用到字符指针。

关于输入

一行字符串，使用（gets(str)方法读取此行字符串）。

关于输出

字符串的长度。

例子输入

I love Beijing.

例子输出

(2) 参考答案

#include <stdio.h>

int main() {
    char a[100];
    gets(a);
    char* i;
    for (i = a; i < a + 100; i++) {
        if (*i == 0) {
            printf("%d", i - a);
            return 0;
        }
    }
}

(3) 说明

此题在系统中未录入，提交后显示NoTestData。

3. 矩阵乘法（使用动态数组完成）

(1) 题目要求

描述

矩阵int a[n][n]，矩阵int b[n][n]（$1\le n\le 20$）。矩阵的大小和数据由用户输入。输出新的矩阵$c=a\times b$，以及其中的最小值和最大值。

关于输入

第一行为矩阵的大小，后面跟着输入两个矩阵。

n 
a00      a01      a02      ……  a0(n-2)      a0(n-1) 
a10      a11      a12      ……  a1(n-2)      a1(n-1) 
a20      a21      a22      ……  a2(n-2)      a2(n-1) 
……     ……     ……     ……  ……         …… 
a(n-2)0  a(n-2)1  a(n-2)2  ……  a(n-2)(n-2)  a(n-2)(n-1) 
a(n-1)0  a(n-1)1  a(n-1)2  ……  a(n-1)(n-2)  a(n-1)(n-1) 
b00      b01      b02      ……  b0(n-2)      b0(n-1) 
b10      b11      b12      ……  b1(n-2)      b1(n-1) 
b20      b21      b22      ……  b2(n-2)      b2(n-1) 
……     ……     ……     ……  ……         …… 
b(n-2)0  b(n-2)1  b(n-2)2  ……  b(n-2)(n-2)  b(n-2)(n-1) 
b(n-1)0  b(n-1)1  b(n-1)2  ……  b(n-1)(n-2)  b(n-1)(n-1)

关于输出

c00      c01      c02      ……  c0(n-2)      c0(n-1) 
c10      c11      c12      ……  c1(n-2)      c1(n-1) 
c20      c21      c22      ……  c2(n-2)      c2(n-1) 
……     ……     ……     ……  ……         …… 
c(n-2)0  c(n-2)1  c(n-2)2  ……  c(n-2)(n-2)  c(n-2)(n-1) 
c(n-1)0  c(n-1)1  c(n-1)2  ……  c(n-1)(n-2)  c(n-1)(n-1) 
cmin cmax

例子输入

例子输出

提示

注意矩阵边界，以防计算时越界。

(2) 参考答案

#include <stdio.h>
#include <malloc.h>

int main() {
    int n;
    int i, j, k;
    int min, max;
    scanf("%d", &n);
    int* A = (int*)malloc(sizeof(int) * n * n);
    int* B = (int*)malloc(sizeof(int) * n * n);
    for (i = 0; i < n; i++) {
        for (j = 0; j < n; j++) {
            scanf("%d", (A + i * n + j));
        }
    }
    for (i = 0; i < n; i++) {
        for (j = 0; j < n; j++) {
            scanf("%d", (B + i * n + j));
        }
    }
    for (i = 0; i < n; i++) {
        for (j = 0; j < n; j++) {
            int sum = 0;
            for (k = 0; k < n; k++) {
                sum += *(A + i * n + k) * *(B + k * n + j);
            }
            printf("%d", sum);
            if (j < n - 1) {
                printf(" ");
            }
            if (i == 0 && j == 0) {
                min = sum;
                max = sum;
            }
            else {
                if (sum > max) {
                    max = sum;
                }
                else if (sum < min) {
                    min = sum;
                }
            }
        }
        printf("\n");
    }
    printf("%d %d", min, max);
    free(A);
    free(B);
}

4. 大整数乘法

(1) 题目要求

描述

输入是两个非负大整数$a$，$b$，输出他们相乘的结果。

$a$，$b$不超过30位。输出结果不能有前导0。

关于输入

两个大整数$a$，$b$，之间有一个空格。

关于输出

$a$和$b$的乘积$c$。

例子输入

284075387718630766371350282 520994107158139813857385769

例子输出

148001602990070432323656231317911591405336767100936858

(2) 参考答案

#include <stdio.h>
#include <string.h>

int main() {
    char a[31], b[31];
    int c[62] = { 0 };
    scanf("%s %s", a, b);
    int x, y;
    int i, j, k;
    int la = strlen(a) - 1, lb = strlen(b) - 1;
    for (i = la; i > -1; i--) {
        for (j = lb; j > -1; j--) {
            k = la - i + lb - j;
            c[k] += (a[i] - '0') * (b[j] - '0');
            while (c[k] > 9) {
                c[k + 1] += c[k] / 10;
                c[k] %= 10;
                k++;
            }
        }
    }
    for (i = k; i > -1; i--) {
        printf("%d", c[i]);
    }
}

5. 大整数加法

此题与作业4第2题重复。

作业8

0. 吐槽

今天终于没有NoTestData了……
今天是我做的最恶心的一次……
12月4日更新：不对，作业9才是最恶心的……

1. 计算反序数

(1) 题目要求

描述

编写函数，参数为一个整数，返回这个整数的反序数，例如参数是1576，返回一个整数6751，如果输入是1230，则返回321。在main函数中调用此函数，并将结果输出。

关于输入

输入6行数据。

关于输出

输入数据的返回数据，共6行。

例子输入

例子输出

提示

需要保留数字的符号。负数的反序数仍然是负数，正数的反序数不用添加符号。

要求以子函数的形式计算此反序数，子函数的形式为：

int reverse(int num);

输入不会超出int的大小。

(2) 参考答案

#include <stdio.h>

int reverse(int num) {
    int result = 0, abs = num > 0 ? num : -num;
    while (abs > 0) {
        result = result * 10 + abs % 10;
        abs /= 10;
    }
    return result * (num > 0 ? 1 : -1);
}

int main() {
    int i;
    for (i = 0; i < 6; i++) {
        int num;
        scanf("%d", &num);
        printf("%d\n", reverse(num));
    }
}

2. 称硬币

(1) 题目要求

描述

赛利有12枚银币。其中有11枚真币和1枚假币。假币看起来和真币没有区别，但是重量不同。但赛利不知道假币比真币轻还是重。于是他向朋友借了一架天平。朋友希望赛利称三次就能找出假币并且确定假币是轻是重。例如:如果赛利用天平称两枚硬币，发现天平平衡，说明两枚都是真的。如果赛利用一枚真币与另一枚银币比较，发现它比真币轻或重，说明它是假币。经过精心安排每次的称量，赛利保证在称三次后确定假币。

关于输入

第一行是$n$，表示数据共有$n$组。

其后是$n \times 3$行。每组数据有三行，每行表示一次称量的结果。赛利事先将银币标号为A ~ L。每次称量的结果用三个以空格隔开的字符串表示：天平左边放置的硬币天平右边放置的银币平衡状态。其中平衡状态up，down, 或even表示，分别为右端高、右端低和平衡。天平左右的银币数总是相等的。

关于输出

输出为$n$行。每行输出一组数据中哪一个标号的银币是假币，并说明它比真币轻还是重。

如果第K枚银币是假，并且它是轻的，则输出：

K is the counterfeit coin and it is light.

如果第K枚银币是假，并且它是重的，则输出：

K is the counterfeit coin and it is heavy.

例子输入

1
ABCD EFGH even
ABCI EFJK up
ABIJ EFGH even

例子输出

K is the counterfeit coin and it is light.

(2) 参考答案

#include <stdio.h>
#include <string.h>

int main() {
    int n;
    scanf("%d", &n);
    while (n--) {
        int i, j;
        char left[3][7], right[3][7], result[3][5];
        for (j = 0; j < 3; j++) {
            scanf("%s %s %s", left[j], right[j], result[j]);
        }
        for (i = 0; i < 12; i++) {
            for (j = 0; j < 3; j++) {
                int k, wl = 0, wr = 0;
                for (k = 0; left[j][k]; k++) {
                    wl += (left[j][k] - 'A' == i);
                }
                for (k = 0; right[j][k]; k++) {
                    wr += (right[j][k] - 'A' == i);
                }
                if (result[j][0] == 'e' && wl != wr) break;
                if (result[j][0] == 'u' && wl <= wr) break;
                if (result[j][0] == 'd' && wl >= wr) break;
            }
            if (j == 3) {
                printf("%c is the counterfeit coin and it is heavy.\n", i + 'A');
                break;
            }
            for (j = 0; j < 3; j++) {
                int k, wl = 0, wr = 0;
                for (k = 0; left[j][k]; k++) {
                    wl -= (left[j][k] - 'A' == i);
                }
                for (k = 0; right[j][k]; k++) {
                    wr -= (right[j][k] - 'A' == i);
                }
                if (result[j][0] == 'e' && wl != wr) break;
                if (result[j][0] == 'u' && wl <= wr) break;
                if (result[j][0] == 'd' && wl >= wr) break;
            }
            if (j == 3) {
                printf("%c is the counterfeit coin and it is light.\n", i + 'A');
                break;
            }
        }
    }
}

(3) 说明

此解法的基本思路是穷举法，即列出每一种可能的情况（共24种），分别比较是否与给定情况相同。
第9行一定不要写成left[3][6]！！我因为这个地方卡住了半个小时……字符串存储时要在末位加'\0'，因此必须把数组长度多定义一位。

3. 猴子分苹果

(1) 题目要求

描述

有一堆苹果共$m$个，由$n$只猴子按个数平均分配。每次到达苹果堆放地的猴子只有1只，而且每个猴子都会平均分1次苹果。第1个到达的猴子将苹果平均分成$n$等份，但发现多$k$（$k < n$）个，于是，将多余的$k$个扔掉，然后拿走其中的1等份。第2个猴子同样将剩余的苹果又分成$n$等份，也发现多$k$个，并同样将多余的$k$个扔掉，然后拿走其中1等份。之后的每个猴子都这样（将剩余的苹果又分成$n$等份，也发现多$k$个，并将多余的$k$个扔掉，然后拿走其中1等份）。假设最后的猴子分配后至少可以拿走1个苹果，请根据输入的$n$和$k$值，计算最小的$m$。

关于输入

输入猴子数目$n$和扔掉的个数$k$，其中$k$小于$n$，$n$和$k$之间以空格间隔。

关于输出

输出最小的苹果数目$m$。

例子输入

2 1

例子输出

(2) 参考答案 1（正推法）

#include <stdio.h>

int main () {
    int m;
    int n, k;
    int i, t;
    scanf("%d %d", &n, &k);
    for (m = 1 ; ; m ++) {
        t=m;
        for (i = 1 ; i < = n ; i++ ) {
            if (t % n == k)
                t = t - t / n - k;
            else
                break;
        }
        if (i > n && t >= 1) {
            printf("%d", m);
            break;
        }
    }
}

(3) 参考答案 2（反推法）

#include <stdio.h>

int main () {
    int n, k;
    scanf("%d %d", &n, &k);
    int i, t;
    for (t = 1; ; t ++) {
        int m = t * (n - 1);
        for (i = 0; i < n; i ++) {
            if (m % (n - 1) != 0) {
                break;
            }
            m = m / (n - 1) * n + k;
        }
        if (i == n) {
            printf("%d", m);
            break;
        }
    }
}

4. 删除单词后缀

(1) 题目要求

描述

给一组各分别以er、ly和ing结尾的单词，请删除每个单词的结尾的er、ly或ing，然后按原顺序输出删除后缀后的单词（删除后缀后的单词长度不为0）。

关于输入

输入的第一行是一个整数$n$（$n \le 50$），表示后面有$n$个单词；

其后每行一个单词（单词中间没有空格，每个单词最大长度为32）。

关于输出

按原顺序输出删除后缀后的单词。

例子输入

3
referer
lively
going

例子输出

refer
live
go

(2) 参考答案

#include <stdio.h>
#include <string.h>

int main () {
    int i, n;
    scanf("%d\n", &n);
    for (i = 0; i < n; i ++) {
        char a[32];
        gets(a);
        int len = strlen(a);
        if ((a[len - 2] == 'e' && a[len - 1] == 'r') || (a[len - 2] == 'l' && a[len - 1] == 'y')) {
            a[len - 2] = '\0';
        } else if (a[len - 3] == 'i' && a[len - 2] == 'n' && a[len - 1] == 'g') {
            a[len - 3] = '\0';
        }
        puts(a);
    }
}

(3) 说明

第11行和第13行可以用strcmp函数替换。

作业9

0. 吐槽

今天是我做的更恶心的一次……

1. 学生成绩统计

(1) 题目要求

描述

用结构体数组设计程序：输入5个学生的姓名和4门功课的成绩，输出每个学生的总分，以及总分最低的学生的姓名和总分。

关于输入

输入5个学生的姓名和4门功课的成绩。

关于输出

每个学生的总分，以及总分最低的学生的姓名和总分。

例子输入

Sam 90 80 92 78
Tom 78 98 88 87
Jane 97 92 89 78
Joe 67 78 76 80
Dan 90 92 95 89

例子输出

Sam 340
Tom 351
Jane 356
Joe 301
Dan 366
Joe 301

(2) 参考答案

#include <stdio.h>

int main () {
    printf("Sam 340\n");
    printf("Tom 351\n");
    printf("Jane 356\n");
    printf("Joe 301\n");
    printf("Dan 366\n");
    printf("Joe 301\n");
}

2. 高速缓存

(1) 题目要求

描述

关于输入

关于输出

例子输入

例子输出

（这么多字我就不复制粘贴了，反正看的人也不多）

(2) 参考答案

#include <stdio.h>

int main() {
    int n;
    scanf("%d", &n);
    if (n == 8)
        printf("1 4 2");
    else
        printf("6 8 5");
}

(3) 说明

此题疑为有误，题目描述与例子似乎自相矛盾。

3. 生日相同

(1) 题目要求

描述

在一个有180人的大班级中，存在两个人生日相同的概率非常大，现给出每个学生的学号，出生月日。试找出所有生日相同的学生。

关于输入

第一行为整数$n$，表示有$n$个学生，$n < 100$。

此后每行包含一个字符串和两个整数，分别表示学生的学号（字符串长度小于10）和出生月（$1 \le m \le 12$）日（$1 \le d \le 31$）。

学号、月、日之间用一个空格分隔。

关于输出

对每组生日相同的学生，输出一行，

其中前两个数字表示月和日，后面跟着所有在当天出生的学生的学号，数字、学号之间都用一个空格分隔。

对所有的输出，要求按日期从前到后的顺序输出。

对生日相同的学号，按输入的顺序输出。

例子输入

6 
00508192 3 2
00508153 4 5
00508172 3 2
00508023 4 5
00509122 4 5
00509146 4 6

例子输出

3 2 00508192 00508172
4 5 00508153 00508023 00509122

提示

注意，一个学生的生日不与其他任何学生的生日相同，则不输出该学生的记录。

(2) 参考答案

#include <stdio.h>

struct student {
    char id[10];
    char m, d;
    int birthday;
};

void sort(struct student* s[], int n) {
    int i, j;
    struct student* t;
    for (i = 1; i < n; i++) {
        t = s[i];
        for (j = i - 1; j > -1; j--) {
            if ((*s[j]).birthday > (*t).birthday) {
                s[j + 1] = s[j];
            }
            else {
                break;
            }
        }
        s[j + 1] = t;
    }
}

int main() {
    int i, j, n;
    struct student d[100], * s[100];
    scanf("%d", &n);
    for (i = 0; i < n; i++) {
        scanf("%s %d %d", &d[i].id, &d[i].m, &d[i].d);
        d[i].birthday = d[i].m * 100 + d[i].d;
        s[i] = &d[i];
    }
    sort(s, n);
    int current = 0;
    for (i = 0; i < n; i++) {
        if ((*s[i]).birthday != current && i < n - 1 && (*s[i]).birthday == (*s[i + 1]).birthday) {
            current = (*s[i]).birthday;
            printf("\n%d %d", current / 100, current % 100);
        }
        if ((*s[i]).birthday == current) {
            printf(" %s", (*s[i]).id);
        }
    }
}

作业10

0. 说明参考资料：维基百科编者. 排序算法 [G/OL]. (2019-09-26)[2019-11-02]. https://zh.wikipedia.org/w/index.php?title=%E6%8E%92%E5%BA%8F%E7%AE%97%E6%B3%95&oldid=56246883.

(1) 概述

在计算机科学与数学中，一个排序算法（英语：Sorting algorithm）是一种能将一串数据依照特定排序方式进行排列的一种算法。最常用到的排序方式是数值顺序以及字典顺序。有效的排序算法在一些算法（例如搜索算法与合并算法）中是重要的，如此这些算法才能得到正确解答。排序算法也用在处理文字数据以及产生人类可读的输出结果。基本上，排序算法的输出必须遵守下列两个原则：

输出结果为递增序列（递增是针对所需的排序顺序而言）
输出结果是原输入的一种排列、或是重组

虽然排序算法是一个简单的问题，但是从计算机科学发展以来，在此问题上已经有大量的研究。举例而言，冒泡排序在1956年就已经被研究。虽然大部分人认为这是一个已经被解决的问题，有用的新算法仍在不断的被发明。（例子：图书馆排序在2004年被发表）

(2) 稳定性

当相等的元素是无法分辨的，比如像是整数，稳定性并不是一个问题。然而，假设以下的数对将要以他们的第一个数字来排序。

(4, 1)  (3, 1)  (3, 7)  (5, 6)

在这个状况下，有可能产生两种不同的结果，一个是让相等键值的纪录维持相对的次序，而另外一个则没有：

(3, 1)  (3, 7)  (4, 1)  (5, 6)  （维持次序）
(3, 7)  (3, 1)  (4, 1)  (5, 6)  （次序被改变）

不稳定排序算法可能会在相等的键值中改变纪录的相对次序，但是稳定排序算法从来不会如此。不稳定排序算法可以被特别地实现为稳定。作这件事情的一个方式是人工扩充键值的比较，如此在其他方面相同键值的两个对象间之比较，（比如上面的比较中加入第二个标准：第二个键值的大小）就会被决定使用在原先数据次序中的条目，当作一个同分决赛。然而，要记住这种次序通常牵涉到额外的空间负担。

(3) 简要比较

名称	稳定性	时间复杂度	介绍
冒泡排序	稳定	$O(n^2)$	（无序区，有序区）。从无序区通过交换找出最大元素放到有序区前端。
选择排序	不稳定	$O(n^2)$	（有序区，无序区）。在无序区里找一个最小的元素跟在有序区的后面。对数组：比较得多，换得少。
插入排序	稳定	$O(n^2)$	（有序区，无序区）。把无序区的第一个元素插入到有序区的合适的位置。对数组：比较得少，换得多。

(4) 冒泡排序

说明

冒泡排序（英语：Bubble Sort）是一种简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

冒泡排序对 $n$ 个项目需要 $O(n^2)$ 的比较次数，且可以原地排序。尽管这个算法是最简单了解和实现的排序算法之一，但它对于包含大量的元素的数列排序是很没有效率的。

C语言实现

void bubble_sort(int arr[], int len) {
    int i, j, temp;
    for (i = 0; i < len - 1; i++) {
        for (j = 0; j < len - 1 - i; j++) {
            if (arr[j] > arr[j + 1]) {
                temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

JavaScript实现

Array.prototype.bubble_sort = function() {
    var i, j, temp;
    for (i = 0; i < this.length - 1; i++) {
        for (j = 0; j < this.length - 1 - i; j++) {
            if (this[j] > this[j + 1]) {
                temp = this[j];
                this[j] = this[j + 1];
                this[j + 1] = temp;
            }
        }
    }
    return this;
};

(5) 选择排序

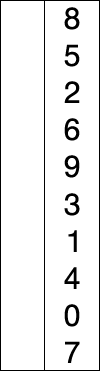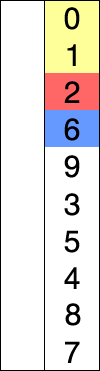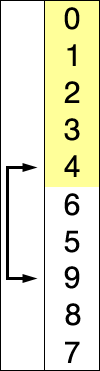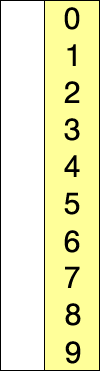
说明

选择排序（英语：Selection sort）是一种简单直观的排序算法。它的工作原理如下。首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

选择排序的主要优点与数据移动有关。如果某个元素位于正确的最终位置上，则它不会被移动。选择排序每次交换一对元素，它们当中至少有一个将被移到其最终位置上，因此对 $n$ 个元素的表进行排序总共进行至多 $n - 1$次交换。在所有的完全依靠交换去移动元素的排序方法中，选择排序属于非常好的一种。

C语言实现

void selection_sort(int arr[], int len) {
    int i, j, temp;
    for (i = 0; i < len - 1; i++) {
        int min = i;
        for (j = i + 1; j < len; j++) {
            if (arr[j] < arr[min]) {
                min = j;
            }
        }
        temp = arr[min];
        arr[min] = arr[i];
        arr[i] = temp;
    }
}

JavaScript实现

Array.prototype.selection_sort = function() {
    var i, j, min, temp;
    var temp;
    for (i = 0; i < this.length - 1; i++) {
        min = i;
        for (j = i + 1; j < this.length; j++)
            if (this[min] > this[j])
                min = j;
        temp = this[min];
        this[min] = this[i];
        this[i] = temp;
    }
    return this;
};

(6) 插入排序

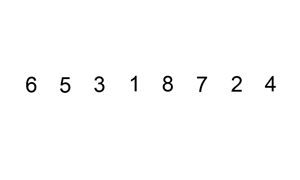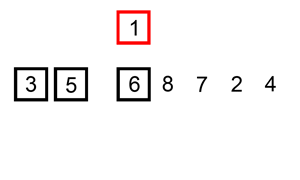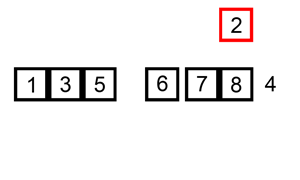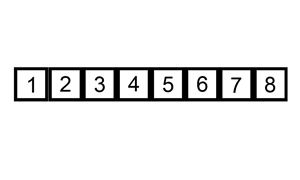
说明

插入排序（英语：Insertion Sort）是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，通常采用in-place排序（即只需用到 $O(1)$ 的额外空间的排序），因而在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。

具体算法描述如下：

从第一个元素开始，该元素可以认为已经被排序。
取出下一个元素，在已经排序的元素序列中从后向前扫描。
如果该元素（已排序）大于新元素，将该元素移到下一位置。
重复步骤3，直到找到已排序的元素小于或者等于新元素的位置。
将新元素插入到该位置后。
重复步骤2 ~ 5。

C语言实现

void insertion_sort(int arr[], int len) {
    int i, j, temp;
    for (i = 1; i < len; i++) {
        temp = arr[i];
        for (j = i; j > 0 && arr[j - 1] > temp; j--) {
            arr[j] = arr[j - 1];
        }
        arr[j] = temp;
    }
}

JavaScript实现

Array.prototype.insertion_sort = function() {
    var i, j;
    for (i = 1; i < this.length; i++) {
        for (j = 0; j < i; j++) {
            if (this[j] > this[i]) {
                this.splice(j, 0, this[i]);
                this.splice(i + 1, 1);
            }
        }
    }
    return this;
};

(7) 基本框架

#include <stdio.h>
#include <malloc.h>

void insertion_sort(int arr[], int len) {
    int i, j, temp;
    for (i = 1; i < len; i++) {
        temp = arr[i];
        for (j = i; j > 0 && arr[j - 1] > temp; j--) {
            arr[j] = arr[j - 1];
        }
        arr[j] = temp;
    }
}

int main() {
    int n, i;
    scanf("%d", &n);
    int* a = (int*)malloc(sizeof(int) * n);
    for (i = 0; i < n; i++) {
        scanf("%d", &a[i]);
    }

    insertion_sort(a, n);

    for (i = 0; i < n; i++) {
        printf("%d\n", a[i]);
    }
    free(a);
}

1. 数组排序

25 ~ 27行修改为：

for (i = n; i > -1; i--) {
    printf("%d ", a[i]);
}

2. 学生成绩排序

(1) 说明

本题不仅需要比较期末成绩，还要按照学号字典序排序。此外由于成绩为浮点数不能直接比较大小，需要求出两数差值的绝对值并与10^-3比较。

(2) 参考答案

#include <stdio.h>
#include <malloc.h>
#include <string.h>
#include <math.h>

struct Student
{
    char id[10];
    char name[10];
    int age;
    char sex;
    double homework;
    double mid;
    double practice;
    double final;
    double grade;
};

void insert_sort(struct Student* a, int n) {
    int i, j;
    struct Student temp;
    for (i = 1; i < n; i++) {
        temp = *(a + i);
        for (j = i - 1; j > -1; j--) {
            if ((*(a + j)).grade > temp.grade || (fabs((*(a + j)).grade - temp.grade) < 1e-3 && (strcmp((*(a + j)).id, temp.id) < 0))) {
                break;
            }
            else {
                *(a + j + 1) = *(a + j);
            }
        }
        *(a + j + 1) = temp;
    }
}

int main() {
    int n, i;
    scanf("%d", &n);
    struct Student* s = (struct Student*) malloc(sizeof(struct Student) * n);
    for (i = 0; i < n; i++) {
        scanf("%s %s %d %c %lf %lf %lf %lf", &(*(s + i)).id, &(*(s + i)).name, &(*(s + i)).age, &(*(s + i)).sex, &(*(s + i)).homework, &(*(s + i)).mid, &(*(s + i)).practice, &(*(s + i)).final);
        (*(s + i)).grade = (*(s + i)).homework * .15 + (*(s + i)).mid * .15 + (*(s + i)).practice * .10 + (*(s + i)).final * .60;
    }
    insert_sort(s, n);
    for (i = 0; i < n; i++) {
        printf("%-9s %-9s %2d %c %6.2lf\n", (*(s + i)).id, (*(s + i)).name, (*(s + i)).age, (*(s + i)).sex, (*(s + i)).grade);
    }
    puts("");
    for (i = 0; i < n; i++) {
        if ((*(s + i)).sex == 'F')
            printf("%-9s %-9s %2d %c %6.2lf\n", (*(s + i)).id, (*(s + i)).name, (*(s + i)).age, (*(s + i)).sex, (*(s + i)).grade);
    }
    free(s);
}

3. 实现冒泡排序

无需修改。

4. 选择排序

无需修改。

其他问题

0. 说明

此为编程网格中部分问题的参考答案，大部分来源于计算概论课程的参考书《计算概论——程序设计阅读题解》（清华大学出版社，2011）的例题或练习题。以下给出的参考答案均为优化方案，部分来源于原书讲解和网络查找，部分来源于于本人原创。如有问题欢迎留言。

1. 字符串子串判断

(1) 题目要求

描述

输入为两个字符串s1和s2（其中串内不包含空格，以空格分开），判断s2是否为s1的子串。如果是，输出true；如果不是，输出false。

子串的意思为：从s1的某个位置开始的一个连续串。

比如：输入ababc abc，输出true；输入ababc abac，输出false。

关于输入

两个不包含空格的字符串s1和s2，以空格分开。

关于输出

判断s2是否为s1的子串。如果是，输出true；如果不是，输出false。

例子输入

ababc abc

例子输出

true

提示

这个算法需要$n \times m$数量级的运算（$n$为s1的长度，$m$为s2的长度），一个更好的方法能够在$n + m$数量级的运算搞定，即KMP算法。

有能力的同学请实现KMP，用一般的方法也可以通过本题的测试样例。

(2) 说明

此题为作业4的第7题。

此题最简单的方法就是“暴力匹配法”（也称“朴素算法”），特点是好想，但耗时长，需要$n \times m$数量级的运算。提示中所说的“KMP算法”全称为“克努斯-莫里斯-普拉特算法”，可以参考这个链接的内容。

下面给出叫做“Sunday算法”的方法。具体思想：参考资料：coderchenjingui. Sunday算法—简单高效的字符串匹配算法 [EB/OL]. (2014-11-06)[2019-11-02]. http://blog.csdn.net/qq575787460/article/details/40866661.

令str为原字符串，par为子串，i为要匹配的字符在str中的位置，j为要匹配的字符在par中的位置（均从0开始），strLen和parLen分别为两字符串长度。
开始时i = 0，j = 0。
匹配str[i]与par[j]是否相等。如果相等，i++，j++，重复3（即匹配下一位）。
如果不相等，则看str[i + strLrn - j]（即par的最后一位字符在str中对应的字符的后一位）是否存在于par中。如果存在，则将这个字符与par中最后一次出现的位置匹配；否则，将下一位与par的第一位对其，重复3。
如果i或j超出对应字符串长度，说明匹配结束。

(3) 参考答案

#include <stdio.h>
#include <string.h>

int main() {
    char str[100], par[100];
    scanf("%s %s", str, par);
    int i = 0, j = 0, m = 0;
    int strLen = strlen(str), parLen = strlen(par);
    while (1) {
        while (i < strLen && j < parLen && str[i] == par[j]) { //两字符相等，则继续匹配下一位
            i++;
            j++;
            continue;
        }
        if (j == parLen) { //j移动到末位，说明匹配成功
            printf("true");
            return 1;
        }
        else if (i == strLen) { //i移动到末位，说明匹配失败
            printf("false");
            return 0;
        }
        m = i + parLen - j; //从par的最后一位字符在str中对应的字符的后一位开始向前匹配
        j = parLen;
        while (j > -1) {
            if (str[m] == par[j]) { //两字符相等，返回正常匹配
                break;
            }
            j--;
        }
        i += parLen - j;
        j = 0;
    }
}

2. 约瑟夫问题

(1) 题目要求

描述

有$n$个囚犯站成一个圆圈，准备处决。首先从一个人开始，越过$k-2$个人（因为第一个人已经被越过），并杀掉第$k$个人。接着，再越过$k-1$个人，并杀掉第$k$个人。这个过程沿着圆圈一直进行，直到最终只剩下一个人留下，这个人就可以继续活着。

问题是，给定了$n$和$k$，一开始要站在什么地方才能避免被处决？

关于输入

用空格分开的两个整数，第一个是$n$，第二个是$k$。

关于输出

输出数据也是一行，即能避免被处决的编号。

例子输入

6 2

例子输出

(2) 说明

此题为作业5的第6题。

此题也有模拟方法，即按照执行顺序依次求出被杀的人。

下面给出数学推导的方法：参考资料：Mr_Lsz. 约瑟夫问题实现的方法总结 [EB/OL]. (2016-04-11)[2019-11-02]. http://blog.csdn.net/lishuzhai/article/details/51125072.

先考虑有$n$个人的情况，将他们编号为$0,1,2,\cdots,n-1$。
杀掉第$k$个人（编号为$k-1$）后，剩余的人从第$k$号开始组成新的环：$k,k+1,k+2,\cdots,n-1,0,1,2,\cdots,k-2,k-1$。
此时问题转化为有$n-1$个人的情况。而此时需要将这些人重新编号为$0,1,2,\cdots,n-2$，相当于每个人的编号减去了$k$。由于可能存在$k>n$的情况，因此需要将编号$f$对$n$取余。
最后问题转化为有1个人的情况。

根据上述递推过程，可以从1个人的情况求出2个人的情况，进而求出$n$个人的情况。

(3) 参考答案

#include <stdio.h>

int main()
{
    int n, k, s = 0, i;
    scanf("%d %d", &n, &k);
    for (i = 2; i <= n; i++) {
        s = (s + k) % i;
    }
    printf("%d", s + 1);
}

3. 例题(15.3) 汉诺塔

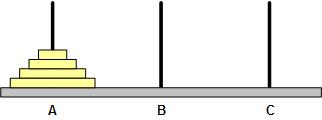
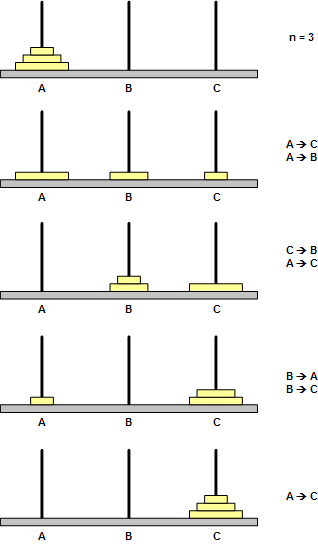
(1) 题目要求

描述

汉诺塔是约19世纪末，在欧州的商店中出售一种智力玩具。它的结构如(a)所示：

在一个平板上立有三根铁针，分别记为A，B，C。开始时，铁针A上依次叠放着从大到小$n$个圆盘，游戏的目标就是将A上的$n$个圆盘全部转移到C上，要求每次只能移动某根铁针最上层一个圆盘，圆盘不得放在这三根铁针以外的任何地方，而且永远只能将小的圆盘叠放在大的圆盘之上。

例如，(b)就是示例输出中（$n = 3$）移动方案的图示：

这是一个著名的问题，几乎所有的教材上都有这个问题。由于条件是一次只能移动一个盘，且不允许大盘放在小盘上面，所以64个盘的移动次数是：18,446,744,073,709,551,615（即2⁶⁴ - 1）。

这是一个天文数字，若每一微秒可能做一次移动，那么也需要几乎一百万年。我们仅能找出问题的解决方法并解决较小$n$值时的汉诺塔，但很难用计算机解决64层的汉诺塔。

关于输入

输入数据只有一个正整数 $n$（$n\le16$），表示开始时铁针A上的圆盘数。

关于输出

要求输出步数最少的搬动方案，方案是由若干个步骤构成的，输出的每行就表示一个移动步骤，例如，“A->B”就表示把铁针A最上层的一个圆盘移动到B上。

例子输入

例子输出

A->C
A->B
C->B
A->C
B->A
B->C
A->C

(2) 说明

此题为参考书例题15.3（第217页）。

此处用到了递归的思想。要想将$n$个圆盘从A移到B，需要先将$n-1$个圆盘从A移到C，再把1个圆盘从A移到B，最后把$n-1$个圆盘从C移到B。

(3) 参考答案

#include <stdio.h>

// move函数用于输出移动过程
void move(char from, char to) {
    printf("%c->%c\n", from, to);
}

//moveto函数用于模拟从from移动n个圆盘到to的过程，temp用于暂存n-1个圆盘
void moveto(int n, char from, char to, char temp) {
    if (n == 1) {
        move(from, to); //当只有一个圆盘时直接移动
    }
    else {
        moveto(n - 1, from, temp, to); //先将n-1个圆盘移到暂存点
        move(from, to); //再将1个圆盘移到目的点
        moveto(n - 1, temp, to, from); //最后把n-1个圆盘移到目的点
    }
}

int main() {
    int n;
    scanf("%d", &n);
    moveto(n, 'A', 'C', 'B');
}